Взаємне розташування прямої і площини

Нехай маємо площину α: Ax+By+Cz+D=0 і пряму l, яка визначається точкою М₀(x₀,y₀,z₀) і направляючим вектором =(α,β,γ). Можна виділити три випадки взаємного розташування прямої і площини:

1.Пряма належить площині.

Розглянемо нормальний вектор площини =(А,В,С) і направляючий вектор =(α,β,γ). Очевидно, що ^ , отже, їх скалярний добуток · = 0. Крім того, довільна точка прямої повинна належати площині, тому координати т.М₀ повинні задовольняти рівняння площини: Ax₀+By₀+Cz₀+D=0.

2.Пряма паралельна до площини.

· = 0 і  Ax₀+By₀+Cz₀+D¹0.

3.Пряма перетинає площину.

· ¹ 0.

Для того, щоб знайти точку перетину прямої і площини, необхідно скласти параметричні р-ня прямої і розв’язати с-му:

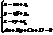. Отримаємо параметр точки перетину. Підставивши його в рівняння прямої, знайдемо координати точки перетину.