
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
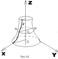
Циліндричні та канонічні поверхні, їх властивості. Класифіфкація поверхонь 2-го порядку.Поверхня, яка разом з будь-якою своєю точкою містить все коло, отримане обертанням цієї точки навколо деякої фіксованої прямої, наз. поверхнею обертання (рис. 18). Пряма, навколо якої виконується обертання, наз. віссю обертання. Якщо поверхню обертання перетинати площинами, перпендикулярними до вісі обертання, то отримаємо кола. Такі кола наз. паралелями поверхні. Площини, які проходять через вісь обертання, перетинають поверхню обертання по лініях, які наз. меридіанами. Конусом 2-го порядкуназ. поверхня, яка в деякій прямо кут. с-мі коор. визнач. Р-ням: Покажемо, що конус склад. із прямих, які проходять через почат. с-ми коор. Нехай т.М0(x0,y0,z0) – довільна точка конуса (23), відмінна від т.О(0,0,0). Тоді координати т.М0 задовол. р-ня конуса отже, Так як змінні x,y,z входять в рівняння конуса лише в парних степенях, то він симетричний відносно координатних площин, осей і початку координат. Дослідимо форму конуса (23) методом перерізів і побудуємо його. 1). Розг. перерізи конуса площиною XOY і || до неї площинами. Їх р-ня z=h. В перетині отримаємо:
а) якщо h=0, то одержимо т.О(0,0,0), b) якщо h ¹ 0, то фігура перетину – еліпс (рис. 21). Конус, який має р-ня (23) – це множина всіх прямих простору, які проходять через т.О і точки будь-якого еліпса з центром в т.Q, яка належ. вісі OZ (Q ¹ О).  У цьому випадку еліпс називається направляючим, авісь OZ називається віссю конуса. Відмітимо, що направляючою конуса наз. довільна лінія розміщена на ньому і для якої викон. умова, що будь-яка прямолінійна твірна перетин. її в одній і тільки одній точці. 2). Розг. перерізи конуса площиною XOZ і || до неї площинами. Їх р-ня y=k. В перетині отримаємо:
a) в площині XOZ, тобто коли k=0, маємо пару прямих, які перетин. в т.О(0,0,0) (рис.21), b) якщо k¹0 то отримаємо гіперболу з дійсною віссю паралельною до OZ. 3). Анало. до другого випадку перерізи отрим. і в площині YOZ та || до неї площинах: x=m.
Переріз конуса з площиною, яка не проходить через т.О може бути як еліпсом, гіперболою, так і параболою (переріз площиною, яка паралельна деякій твірній). Таким чином криві другого порядку (еліпс, гіперболу, параболу) можна розглядати як перерізи конуса другого порядку площинами. Тому їх часто наз. конічними перерізами. Поверхня, яка разом з будь-якою своєю точкою містить і всю пряму, яка проход. через цю точку, паралельно до деякого вектора Циліндрич. поверхню можна отрим., якщо провести через деяку криву Циліндр другого порядку може бути (в залежності від направляючої) еліптичним, гіперболічним, параболічним, а також виродженим циліндром, який розпадається на пару площин, що перетин., пару || площин, пару площин що співпадають. Еліптичним циліндромназ. поверхня, яка в деякі прямо кут. с-мі коор. визнач. р-ням: Дослідимо форму еліптичного циліндраметодом перерізів і побудуємо його. 1). Розг. перерізи еліптичного циліндраплощиною XOY і || до неї площинами:
а). Якщо b). Якщо с). Якщо 3). Перетин еліптич. циліндра зплощиною YOZ і || до неї площинами повністю аналогіч. до попереднього (рис.26). Як бачимо для побудови циліндра можна і не використовувати метод перерізів, а просто побудувати направляючу і провести твірні, || до вісі циліндра. Гіперболічним циліндром (рис.27)наз. поверхня, яка в деякі прямо кут. с-мі коор. визнач. р-ням: Параболічним циліндром (рис.28)наз. поверхня, яка в деякі прямо кут. с-мі коор. визнач. р-ням:
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 875. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
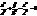 (23)
(23) . Розгул. т.М(tx0,ty0,tz0), де tÎ R. Т.М також належ. конусу, оскільки
. Розгул. т.М(tx0,ty0,tz0), де tÎ R. Т.М також належ. конусу, оскільки 
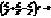 . Таким чином разом з т.М0 конусу належ. вся пряма, яка проходить через поч.. коор. і має направляючий вектор
. Таким чином разом з т.М0 конусу належ. вся пряма, яка проходить через поч.. коор. і має направляючий вектор 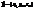 . Отже, конус можна розг. як множину деяких прямих, які проходять через т.О, які наз. твірними. Т.О наз. вершиною конуса.
. Отже, конус можна розг. як множину деяких прямих, які проходять через т.О, які наз. твірними. Т.О наз. вершиною конуса. або
або  . Можливі випадки:
. Можливі випадки: або
або 
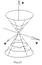 Якщо в р-ні (23) a=b, то конус наз. конусом обертання, або круговим конусом.
Якщо в р-ні (23) a=b, то конус наз. конусом обертання, або круговим конусом. наз. циліндричною.
наз. циліндричною. (направляючу) прямі лінії (твірні), які || до
(направляючу) прямі лінії (твірні), які || до  . Якщо
. Якщо  належ. циліндрич. поверхні (її координати задовол. р-ня F(x,y)=0), то цій поверхні буде належ. і т.
належ. циліндрич. поверхні (її координати задовол. р-ня F(x,y)=0), то цій поверхні буде належ. і т. 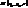 (так як її коор. задовол. це ж р-ня F(x,y)=0) отже, поверхні буде належ. і вся пряма, яка || до вісі OZ.
(так як її коор. задовол. це ж р-ня F(x,y)=0) отже, поверхні буде належ. і вся пряма, яка || до вісі OZ.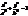 . (28)
. (28)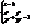 – еліпс.
– еліпс.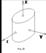 2). В перетині еліптич. циліндра зплощиною XOZ і || до неї площинами отрим.:
2). В перетині еліптич. циліндра зплощиною XOZ і || до неї площинами отрим.: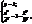 або
або 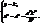
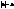 то маємо пару прямих, що співпали (будуємо пряму паралельну до вісі OZ) (рис 26).
то маємо пару прямих, що співпали (будуємо пряму паралельну до вісі OZ) (рис 26).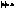 маємо порожню множину.
маємо порожню множину. отримаємо пару паралельних прямих (які паралельні до вісі OZ).
отримаємо пару паралельних прямих (які паралельні до вісі OZ). . (29)
. (29)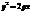 . (30)
. (30)
