
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Пряма в прямокутній системі координатВсі р-ня прямої (23) – (28), які ми отримали в афінній с-мі коор., мають місце і в прямокутній с-мі. Виведемо ще два р-ня прямої, які пов’язані з поняттями перпендикулярності, і тому мають місце тільки в прямокутній с-мі коор. Вектор
Нехай пряма d в прямокутній с-мі коор. задана т.М0(x0,y0), і нормальним вектором Тоді вектор Відмітимо, що для прямої, заданої загальним рівнянням Ax+By+C=0, нормальний вектор 8. Нормальне рівняння прямої:
Скориставшись р-ням (29) отримаємо: cosφ(x–ρcosφ)+sinφ(y–ρsinφ)=0, або xcosφ+ysinφ – ρ=0 (30) Очевидно, що для того, щоб із загального р-ня отримати нормальне р-ня, потрібно розділити його почленно на довжину нормального вектора ( таким чином ми отримаємо одиничний нормальний вектор 
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 471. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ≠
≠  наз. нормальним вектором прямої, якщо він перпендикулярний до будь-якого її направляючого вектора.
наз. нормальним вектором прямої, якщо він перпендикулярний до будь-якого її направляючого вектора. 7. Рівняння прямої, заданої точкою і нормальним вектором.
7. Рівняння прямої, заданої точкою і нормальним вектором. = (А,В). Виберемо довільну т.М(x,y) на прямій d (рис.23).
= (А,В). Виберемо довільну т.М(x,y) на прямій d (рис.23).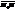 =(x-x0, y-y0) перпендик. до вектора
=(x-x0, y-y0) перпендик. до вектора  , отже, їх скаляр. добуток
, отже, їх скаляр. добуток  ·
·  =(-В, А) (
=(-В, А) (  =0).
=0). Нехай пряма лінія задана в прямокутній с-мі коор. одиничним нормальним вектором
Нехай пряма лінія задана в прямокутній с-мі коор. одиничним нормальним вектором  =ρ
=ρ