
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Перетворення подібності. Гомотетія. Аналітичне задання подібності. Група подібності та її властивості.Перетворення площини наз. перетворенням подібності (подібністю), якщо існує число Якщо Тобто рух – це частковий випадок перетворення подібності. Розг. приклад перетворення подібності, відмінного від руху. Зафіксуємо точку Кожній точці М площини поставимо у відповідність точку
Покажемо, що гомотетія є перетвор.подібності. Розг. ще одну т.N площ. та її образ – т.
Таким чином гомотетія є перетвор.подібності з коефіцієнтом k= · якщо · якщо · якщо
Нехай точка М має координати x, y, а точка
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 626. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
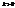 таке, що для будь-яких точок А і В і їх образів
таке, що для будь-яких точок А і В і їх образів  і
і  виконується умова
виконується умова 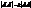 .
.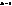 , то отримаємо рух площини.
, то отримаємо рух площини. і число
і число 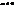 .
. таку, щоб виконувалась рівність:
таку, щоб виконувалась рівність: 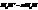 (2) (рис.5).
(2) (рис.5).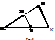 Таке перетвор. площини наз. гомотетією з центром в т.
Таке перетвор. площини наз. гомотетією з центром в т.  (рис.5). Тоді
(рис.5). Тоді 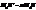 .
.
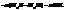 Отже,
Отже,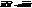 (3)
(3) .
.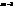 , то маємо тотожне перетворення,
, то маємо тотожне перетворення,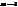 , то це перетворення – центральна симетрія відносно т.
, то це перетворення – центральна симетрія відносно т. 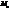 ,
, , то гомотетія відмінна від руху.
, то гомотетія відмінна від руху.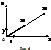 Задамо на площині с-му коор.
Задамо на площині с-му коор. 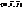 , і розг. т.М та її образ т.
, і розг. т.М та її образ т.  при гомотетії з центром в т.О(0,0) (рис.6). Одерж. аналітич. задання такої гомотетії.
при гомотетії з центром в т.О(0,0) (рис.6). Одерж. аналітич. задання такої гомотетії.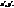 Тоді за означенням гомотетії
Тоді за означенням гомотетії 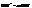 . Перейшовши до координат, отримаємо:
. Перейшовши до координат, отримаємо: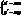 (4)
(4)