
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Відстань від точки до площиниНехай дана точка М0(x0,y0,z0), а площина задана загальним рівнянням Ax+By+Cz+D=0. Нормальний вектор площини d = | Оскільки точка Н належить площині, то її координати задовольняють рівняння (37), тому –Ax–By–Cz=D і d = Пряма лінія у просторі Так як і на площині пряму лінію у просторі можна задати двома точками або точкою і направляючим вектором. Крім того, її можна задати як перетин двох площин. 1. Канонічні рівняння прямої (за точкою і направляючим вектором) Нехай в афінній с-мі коор.пряма проходить через т.М0 (x0,y0,z0) і має направляючий вектор Якщо одна із координат направляючого вектора, наприклад, α=0, то (42) можна записати: Аналогічно, якщо β=0 або γ=0. Якщо α=β=0, то отримаємо Відмітимо, що в останньому випадку ми отримали пряму лінію, задану як перетин двох площин, які паралельні до координатних площин. 2. Рівняння прямої за двома точками Нехай пряма проходить через точки М1(x1,y1,z1) і М2(x2,y2,z2). Тоді вектор  3. Параметричні рівняння прямої Нехай пряма задана точкою М0 (x0,y0,z0) і направляючим вектором x–x0 = α t ; y–y0 = β t; z–z0 = γ t, або:
4. Рівняння прямої, заданої як перетин двох площин. Розглянемо дві площини, задані р-нями α: A1x+B1y+C1z+D1=0 і β: A2x+B2y+C2z+D2=0, причому їх нормальні вектори неколінеарні (умова перетину), отже, коефіцієнти біля змінних в рівняннях площин не пропорційні. Перетин таких площин визначатиме пряму, яку можна задати системою:
причому Взаємне розташування двох прямих у просторі Нехай задано прямі l1 і l2, які визначаються відповідно: l1 точкою M1 і направляючим вектором Прямі у просторі можуть бути розташовані таким чином: 1.Співпадають: Тоді 2.Паралельні: 3.Перетинаються: 4.Мимобіжні: Вектори |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 645. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 =(А,В,С). Розглянемо такий вектор
=(А,В,С). Розглянемо такий вектор 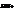 ||
||  1. Отже,
1. Отже, 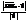 =
= 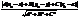 .
.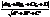 (40).
(40). =(α,β,γ). Виберемо на прямій довільну т.М (x,y,z) і розглянемо вектор
=(α,β,γ). Виберемо на прямій довільну т.М (x,y,z) і розглянемо вектор 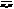 =(x-x0 ,y-y0 ,z-z0). Очевидно, що
=(x-x0 ,y-y0 ,z-z0). Очевидно, що 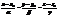 . (42)
. (42)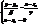 .
.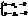 . Аналогічно для β=γ=0 та α=γ=0.
. Аналогічно для β=γ=0 та α=γ=0. =
= 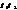 – є направляючим вектором прямої. Скориставшись р-ням (42) отримаємо:
– є направляючим вектором прямої. Скориставшись р-ням (42) отримаємо: 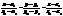 . (43)
. (43)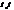 =(x–x0,y–y0,z–z0).
=(x–x0,y–y0,z–z0). 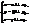 (44)
(44)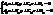 , (45)
, (45)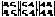 ) є направляючим вектором прямої.
) є направляючим вектором прямої. 2,
2,