
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Пряма лінія в афінній системі координатБудь-який вектор, відмінний від нуль-вектора, наз. направляючим вектором прямої, якщо він || до даної прямої. Сукупність всіх направляючих векторів конкретної прямої а утворює одновимірний векторний простір. Пряму лінію на площині в афінній с-мі коор. можна задати точкою і направляючим вектором, або двома точками. 1.Рівняння прямої за точкою і направляючим вектором:
Отримане р-ня наз. канонічним рівнянням прямої. Його можна записати 2. Параметричні рівняння прямої: Як і в попередньому випадку пряму задано т.М0(x0,y0), та направляючим вектором
3. Рівняння прямої за двома точками. Дано дві точки прямої М1(x1,y1) та М2(x2,y2) (рис.19). Тоді вектор 4. Рівняння прямої у відрізках на осях.
bx+ay = ab. Так як а і b не рівні нулю, то розділивши обидві частини рівності на ab, отримаємо рівняння прямої „у відрізках”: 
Нехай в афінній с-мі коор. задана пряма а, яка перетинає вісь ординат і проходить через т.М0(x0,y0), та має направляючий вектор Число Покажемо, що кутовий коефіцієнт не залежить від вибору направляючого вектора. Нехай пряма а має ще один направляючий вектор Якщо за т.М взяти точку перетину прямої з віссю ординат – В(0,b), то р-ня прямої з кутовим коефіцієнтом приймає вигляд: Якщо пряма задана в прямокутній с-мі коор., то кутовий коефіцієнт k має простий геометричний зміст: β = | 6. Загальне рівняння прямої Всі отримані нами рівняння прямої є р-нями першої степені від двох змінних, тобто їх можна записати загальним рівнянням: Ax+By+C=0. (28) Теор14.Рівняння Ax+By+C=0,(де А і В не рівні нулю одночасно) в афінній системі координат на площині визначає пряму лінію. Причому вектор Доведення: Очевидно, що існує т.М(x0, y0), координати якої задовольняють р-ня (28). Отже, Аx0+Вy0+С=0. Звідси С = – Аx0 – Вy0. Підставивши значення С в рівність (28), отримаємо: Аx+Вy–Аx0–Вy0=0, або А(x–x0)+В(y–y0)=0. Отримали р-ня прямої вигляду (23¢), де координати направляючого вектора α = – В, а β = А. Отже, р-ня (28) визначає пряму, яка проходить через т.М(x0, y0) і має направляючий вектор |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 436. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 Нехай в афінній с-мі. коор. (О,
Нехай в афінній с-мі. коор. (О,  ,
,  ) задано т. М0(x0,y0), та направляючий вектор
) задано т. М0(x0,y0), та направляючий вектор  =(α,β) прямої а (рис.18). Потрібно знайти р-ня прямої а. Виберемо на прямій довільну т.М(x,y). Тоді
=(α,β) прямої а (рис.18). Потрібно знайти р-ня прямої а. Виберемо на прямій довільну т.М(x,y). Тоді 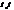 =(x-x0, y-y0);
=(x-x0, y-y0); 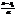 =
= 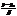 . (23)
. (23) = 0 (23¢)
= 0 (23¢) . Перейдемо до координат:
. Перейдемо до координат: x – x0= t·α, y – y0= t·β; отримаємо параметричні рівняння прямої:
x – x0= t·α, y – y0= t·β; отримаємо параметричні рівняння прямої: (24)
(24)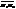 буде направляючим для прямої М1М2. Аналогічно попередньому розг. довільну т.М(x,y) цієї прямої. Тоді
буде направляючим для прямої М1М2. Аналогічно попередньому розг. довільну т.М(x,y) цієї прямої. Тоді  =(x–x1, y–y1). Так як вектори
=(x–x1, y–y1). Так як вектори 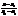 =
=  (25)
(25) Нехай пряма а не проходить через початок с-ми коор. Тоді вона перетинає вісі координат у точках А та В, які відповідно мають координати А(а,0), В(0,b) (рис.20). Скориставшись р-ням (25) отримаємо:
Нехай пряма а не проходить через початок с-ми коор. Тоді вона перетинає вісі координат у точках А та В, які відповідно мають координати А(а,0), В(0,b) (рис.20). Скориставшись р-ням (25) отримаємо: 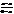 =
=  , або
, або 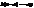 , bx – ba = – ay ,
, bx – ba = – ay , +
+  =1, (26)де а і b направлені відрізки на осях системи координат (можуть бути і від¢ємними).
=1, (26)де а і b направлені відрізки на осях системи координат (можуть бути і від¢ємними). 5. Р-ня прямої з кутовим коефіцієнтом.
5. Р-ня прямої з кутовим коефіцієнтом.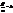 наз. кутовим коеф. прямої а.
наз. кутовим коеф. прямої а.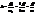 , тобто кутовий коефіцієнт не залежить від направляючого вектора. Поділивши обидві частини рівності (23¢) на α отримаємо: y – y0=k (x – x0) (27)
, тобто кутовий коефіцієнт не залежить від направляючого вектора. Поділивши обидві частини рівності (23¢) на α отримаємо: y – y0=k (x – x0) (27) . (27¢)
. (27¢) | sin φ, α = |
| sin φ, α = |