
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Рух 1 і 2 роду. Класифікація рухів площини та їх аналітичне задання. Групи рухів та їх підгрупи.Зупинимося на властивостях руху. 1. Рух переводить пряму у пряму, причому || прямі в || прямі. 2. Рух зберігає просте відношення трьох точок. 3. Рух зберігає поняття „лежати між”. 4.Рух переводить півплощину з границею l в півплощину з границею 5. Рух переводить промінь в промінь. 6. Рух переводить кут в рівний йому кут (так як переводить трикутник в рівний йому трикутник). Перетворення площини зберіг. орієнтацію площини, якщо репер R і його образ Коли рух орієнтація площини не змінює, то він наз. власним (рухом 1-го роду), якщо змінює – невласним (рухом 2-го роду). Отримаємо аналітичне задання руху. Нехай g – даний рух. Розглянемо на площині ортонормов. репер R= Одерж. аналіт. задання руху значить вираз. коор. т. Так як рух g задано, то за теор2 ортонормов репер R= Отже, фактично одержуємо звичайну задачу перетвор. прямокут. с-ем коор.: т. Такі формули мають вигляд:
де Класифікацію рухів площини провед. в залеж. від наявності інваріантних точок і прямих, і одержимо аналітичне задання конкретних рухів. Інваріантна точка (нерухома) перетворення – це точка, яка переходить в себе при даному перетворенні. Інваріантна пряма (нерухома) – це пряма, кожна точка якої переходить в точку цієї ж прямої при даному перетворенні .  Власні рухи: а) тотожне перетворення. При такому перетвор. повороту немає, отже
б) поворот на
в) центральна симетрія.Тут
г) паралельне перенесення. Маємо
Невласні рухи: а) осьова симетрія.Повороту немає, тому
б) ковзна симетрія (симетрія відносно прямої, а потім перенесення на Тут
Нам відомо, що всі перетворення площини утворюють групу Перевіримо замкненість: Операція тут – композиція рухів. Потрібно показати, що композиція будь-яких двох рухів є рух. Розг дві точки А і В площини. Нехай рух g відображає їх в точки Очевидно, що для будь-якого руху Розг. множину всіх власних рухів Невласні рухи не утвор. групу, так як не викон. перша умова (замкненість). Дійсно, послідов. викон.двох невласних рухів буде власним рухом. Нехай Т – множина всіх || переносів площини. Тоді Т – підмножина групи власних рухів Отже, всі || перенесення утвор. групу Т – підгрупу груп D і Існують і скінченні підгрупи групи рухів. Розглянемо 1. Очевид., що якщо рух f відображу. фігуру F в себе і рух g відображу. F в себе, то і послідовне викон. рухів f і g (f*g) відображу. фігуру F в себе, тому операція замкнена (1-ша умова). 2. Ясно також, що для будь-якого руху, що відображу. фігуру F в себе, існує обернений елемент (рух назад) який відображу. F в себе (2-га умова). Отже, Якщо Якщо F – коло або смуга, то Можна розг. і групу
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 832. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , де
, де  однаково орієнтовані і змінює орієнтацію площини, якщо R і
однаково орієнтовані і змінює орієнтацію площини, якщо R і 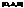 . Познач. (х, у) координати довільної т.М в цьому репері, а через (
. Познач. (х, у) координати довільної т.М в цьому репері, а через ( 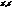 ) координати її образа при рухові g в цьому ж репері R .
) координати її образа при рухові g в цьому ж репері R .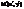 в репері R ч/з х, у.
в репері R ч/з х, у.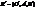 .
. 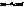 , причому
, причому 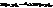 .
. в старому репері R має координати
в старому репері R має координати  – х, у. Потрібно виразити
– х, у. Потрібно виразити 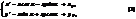
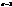 , якщо репери R і
, якщо репери R і 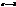 , при рухах другого роду.
, при рухах другого роду.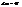 і перенес. немає, тому
і перенес. немає, тому 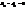 . Підстав. ці знач. в ф-лу (1) отрим. :
. Підстав. ці знач. в ф-лу (1) отрим. :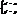 . Тобто інваріантними залишаються всі точки і всі прямі площини.
. Тобто інваріантними залишаються всі точки і всі прямі площини.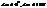 . Нехай центром обертання є т.О(0,0). Тоді
. Нехай центром обертання є т.О(0,0). Тоді 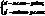 Інваріантною є єдина точка – точка навколо якої викон. обертання. Інваріантних прямих немає.
Інваріантною є єдина точка – точка навколо якої викон. обертання. Інваріантних прямих немає.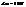 . Нехай центром симетрії є т.О(0,0), тоді
. Нехай центром симетрії є т.О(0,0), тоді 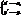 Інваріантна точка – центр симетрії. Інваріантні прямі – прямі, що проходять через центр симетрії.
Інваріантна точка – центр симетрії. Інваріантні прямі – прямі, що проходять через центр симетрії.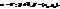 Аналітичне задання:
Аналітичне задання: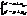 Інваріантних точок немає, інваріантні прямі – прямі, що паралельні до
Інваріантних точок немає, інваріантні прямі – прямі, що паралельні до  .
.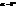 . Якщо
. Якщо 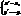 Інваріантні точки – всі точки вісі симетрії. Інваріантні прямі – сама вісь симетрії і всі прямі, які перпендикулярні до неї.
Інваріантні точки – всі точки вісі симетрії. Інваріантні прямі – сама вісь симетрії і всі прямі, які перпендикулярні до неї.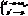 Інваріантні точки – точки вісі симетрії, інваріантна пряма – вісь симетрії.
Інваріантні точки – точки вісі симетрії, інваріантна пряма – вісь симетрії. . Позначимо D – множину всіх рухів площини. Так як рухи площини – це перетворення площини, то для того, щоб вони утворювали групу, згідно теор1, досить перевірити дві умови: замкненість і існув обернено елемента на множині рухів.
. Позначимо D – множину всіх рухів площини. Так як рухи площини – це перетворення площини, то для того, щоб вони утворювали групу, згідно теор1, досить перевірити дві умови: замкненість і існув обернено елемента на множині рухів. і
і  . Тоді за означенням руху
. Тоді за означенням руху 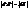 . Нехай рух f відображає точки
. Нехай рух f відображає точки  і
і  відповідно, тоді
відповідно, тоді 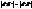 . Отже,
. Отже, 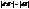 . Таким чином послідовне виконання двох рухів g і f, тобто їх композиція – теж рух, так як зберігає відстань між точками.
. Таким чином послідовне виконання двох рухів g і f, тобто їх композиція – теж рух, так як зберігає відстань між точками. існує обернений рух
існує обернений рух  . Тому всі рухи площини утвор. групу D, яка є підгрупою групи
. Тому всі рухи площини утвор. групу D, яка є підгрупою групи  площини. Очевидно, що композиція двох власних рухів є власним рухом (орієнтація площини не змінюється) і для будь-якого власного руху g існує обернений
площини. Очевидно, що композиція двох власних рухів є власним рухом (орієнтація площини не змінюється) і для будь-якого власного руху g існує обернений 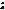 існує обернений то Т – група переносів площини.
існує обернений то Т – група переносів площини. утвор. групу, підгрупу
утвор. групу, підгрупу  – множину всіх рухів площини, які переводять фігуру F в себе.
– множину всіх рухів площини, які переводять фігуру F в себе. поворотів правильного n–кутника. Її елементи – повороти многокутнока навколо його центра О, які відображ. многокутник в себе. Ця група склад.з степенів одного з своїх елементів (циклічна).
поворотів правильного n–кутника. Її елементи – повороти многокутнока навколо його центра О, які відображ. многокутник в себе. Ця група склад.з степенів одного з своїх елементів (циклічна).