Лінійні операції над векторами та їх властивості. Скалярний добуток векторів його властивості та застосування.
Сумою двох векторів  = =  і і  = =  наз. вектор наз. вектор  = =  , який є діагоналлю паралелограма, побудов. на векторах , який є діагоналлю паралелограма, побудов. на векторах  і і  (рис.1). (рис.1).
 + +  = =  + +  = =  = =  . Так як . Так як  = =  , то , то  + +  = =  . .
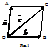 Правило додавання векторів, яке визначається цією формулою, називається правилом трикутника. Правило додавання векторів, яке визначається цією формулою, називається правилом трикутника.
Властивості додавання:
 1. Для будь-яких векторів 1. Для будь-яких векторів  , ,  і і  : :  +( +(  + +  )=( )=(  + +  )+ )+  (асоціатив. закон додавання). (асоціатив. закон додавання).
Доведення: (рис.2).
 +( +(  + +  )= )=  +( +(  + + 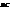 )= )=  + +  = =  , ,
(  + +  )+ )+  =( =(  + +  )+ )+ 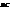 = =  + + 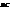 = =  . .
2. Для будь-яких векторів  і і  : :  + +  = =  + +  ( комутатив. закон додавання ). ( комутатив. закон додавання ).
Доведення:  + +  = =  + +  = =  (рис.1), (рис.1),  + +  = =  + +  = =  . .
3. Існує  вектор , такий, що для будь-якого вектор , такий, що для будь-якого  : :  + +  = =  . .
Доведення: Нехай  = =  , тоді за правилом трикутника , тоді за правилом трикутника  = =  , так як , так як  + +  = =  + +  = =  = =  . .
4. Існує вектор  ′, такий, що для будь-якого вектора ′, такий, що для будь-якого вектора  : :  + +  ′ = ′ =  . .
Доведення: Нехай  = =  ; тоді ; тоді  + +  = =  = =  , отже, , отже,  ′= ′=  (це вектор протилежний до (це вектор протилежний до  ). ).
Різницею двох векторів  – –  наз. такий вектор наз. такий вектор  , що , що  + +  = =  . .
 Різниця будь-яких векторів Різниця будь-яких векторів  і і  завжди існує і визначається однозначно, так як завжди існує і визначається однозначно, так як  – –  = =  +(– +(–  ). Вектор – ). Вектор –  існує і визначається однозначно, сума двох векторів існує і визначається однозначно, сума двох векторів  і (– і (–  ) існує і визначається однозначно. Отже, щоб від вектора ) існує і визначається однозначно. Отже, щоб від вектора  відняти вектор відняти вектор  потрібно до вектора потрібно до вектора  додати вектор – додати вектор –  (рис.3). (рис.3).
 – –  = =  – –  = =  + +  = =  + +  = =  = =  .Маємо: .Маємо:  – –  = =  (рис.3). (рис.3).
Добутком вектора  на дійсне число λ називається такий вектор на дійсне число λ називається такий вектор  , для якого виконуються умови: 1. | , для якого виконуються умови: 1. |  |=| λ | | |=| λ | |  |– довжина вектора |– довжина вектора  ; 2. ; 2.  ↑↑ ↑↑  – коли λ >0; 3. – коли λ >0; 3.  ↑↓ ↑↓  – коли λ <0; – коли λ <0;
Властивості:Для будь-яких дійсних чисел α і β та векторів  , ,  мають місце рівності: 1. 1· мають місце рівності: 1. 1·  = =  ; (–1)· ; (–1)·  = – = –  ; ;
2. α·(  + +  ) = α· ) = α·  +α· +α·  ; ;
3. (α+β)·  = α· = α·  +β· +β·  ; ;
4. α·(β·  ) = (α·β)· ) = (α·β)·  . .
Доведення:
1. Властивість випливає з означення добутку вектора на число.
 2.α·( 2.α·(  + +  )=α·( )=α·(  + +  )=α· )=α·  = =  (рис.4). (рис.4).
α·  +α· +α·  =α· =α·  +α· +α·  = = 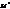 + + 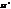 = =  (рис.4). (рис.4).
Отже, ми отрим. гомотетію з центром в т.О та коефіцієнтом α. При гомотетії паралелограм ACBO перейшов у паралелограм A  C C  B B  O , діагональ OC перейшла в OC O , діагональ OC перейшла в OC  . .
3. Справедливість третьої властив. випливає з того, що вектори α  і β і β  колінеарні. Їх додавання фактично зводиться до додавання чисел α·ç колінеарні. Їх додавання фактично зводиться до додавання чисел α·ç  çі β·ç çі β·ç  çта побудови вектора отриманої довжини, який колінеарний вектору çта побудови вектора отриманої довжини, який колінеарний вектору  . .
4. Очевидно, що вектори α(β  і (αβ) і (αβ)  співнаправлені, так як в обох випадках добуток чисел α і β має однаковий знак. Покаж., що і модулі їх рівні. Дійсно, за означенням добутку вектора на число отримаємо: співнаправлені, так як в обох випадках добуток чисел α і β має однаковий знак. Покаж., що і модулі їх рівні. Дійсно, за означенням добутку вектора на число отримаємо:
│α·(β·  )│=│α│∙│(β· )│=│α│∙│(β·  )│=│α│∙│β│∙│ )│=│α│∙│β│∙│  │. │.
│(α·β)·  │=│(α·β)│∙│ │=│(α·β)│∙│  │=│α│∙│β│∙│ │=│α│∙│β│∙│  │. │.
Відклад. ненульові вектори  і і  від точки О: від точки О:  = =  , ,  = =  (рис.7). Кут АОВ називається кутом між векторами (рис.7). Кут АОВ називається кутом між векторами  і і  і позначається ( і позначається (  ˆ ˆ  ) = α. Кут між векторами вибирається меншим або рівним p . ) = α. Кут між векторами вибирається меншим або рівним p .
Для розв’яз. метричних задач використав. Ортонормов. базис  , ,  , ,  , де , де 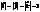 і всі кути між цими векторами рівні 900 і всі кути між цими векторами рівні 900
Скалярним добутком двох ненульових векторів  і і  наз. число яке = модулів цих векторів на косинус кута між ними (познач. наз. число яке = модулів цих векторів на косинус кута між ними (познач.  ∙ ∙  = | = |  |∙| |∙|  |∙cosα). |∙cosα).
Скалярний добуток нуль-вектора і довільн. вектора покладається рівним нулю.
З означ. скалярного добутку отримаємо формулу для знаходження косинуса кута між векторами: cos (  ˆ ˆ  ) = ) =  (4) (4)
Теор8Скалярний добуток векторів  =(а1,а2 ,а3 ), =(а1,а2 ,а3 ),  =(b1,b2 ,b3 ), заданих в ортонормов. базисі пр-ру, виражається формулою: =(b1,b2 ,b3 ), заданих в ортонормов. базисі пр-ру, виражається формулою:  ∙ ∙  =а1b1+а2b2+а3b3 (5) =а1b1+а2b2+а3b3 (5)
Доведення: Запишемо розклади даних векторів по базису:
 = а1 = а1  + а2 + а2  + а3 + а3  і і  = b1 = b1  + b2 + b2  + b3 + b3  . .
Тоді  ∙ ∙  = (а1 = (а1  + а2 + а2  + а3 + а3  )∙(b1 )∙(b1  + b2 + b2  + b3 + b3  )= )=
= а1 b1 (  ∙ ∙  )+ а1 b2 ( )+ а1 b2 (  ∙ ∙  )+ а1 b3 ( )+ а1 b3 (  ∙ ∙  )+ а2 b1 ( )+ а2 b1 (  ∙ ∙  )+ а2 b2 ( )+ а2 b2 (  ∙ ∙  )+ )+
+ а2 b3 (  ∙ ∙  )+ а3 b1 ( )+ а3 b1 (  ∙ ∙  )+ а3 b2( )+ а3 b2(  ∙ ∙  )+ а3 b3 ( )+ а3 b3 (  ∙ ∙  ). А так як скалярні добутки ). А так як скалярні добутки  ∙ ∙  = =  ∙ ∙  = =  ∙ ∙  =1, а =1, а  ∙ ∙  = =  ∙ ∙  = =  ∙ ∙  =0 , то отримаємо, що =0 , то отримаємо, що  ∙ ∙  = а1b1+а2 b2+а3 b3. = а1b1+а2 b2+а3 b3.
Наслід9. Вектори  =(а1, а2 , а3 ); =(а1, а2 , а3 );  =(b1, b2 , b3 ) задані в ортонормов. базисі простору, взаємно перпендикулярні ↔, коли а1 b1+а2 b2+а3 b3 = 0. =(b1, b2 , b3 ) задані в ортонормов. базисі простору, взаємно перпендикулярні ↔, коли а1 b1+а2 b2+а3 b3 = 0.
Розгул. скалярний добуток вектора  на себе: на себе:   = | = |  |2 . наз. скалярним квадратом вектора |2 . наз. скалярним квадратом вектора  і познач. і познач.  2. Звідси отрим. ф-лу для обчислення модуля вектора за його координат.: | 2. Звідси отрим. ф-лу для обчислення модуля вектора за його координат.: |  | = | =  = = 
Наслід10.Косинус кута α між ненульовими векторами  =(а1, а2, а3) і =(а1, а2, а3) і  =(b1, b2, b3), заданими в ортонормованому базисі, визначається формулою: cos α = =(b1, b2, b3), заданими в ортонормованому базисі, визначається формулою: cos α = 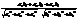 . .
Властивості скалярного добутку:
1.  ∙ ∙  = =  ∙ ∙  (комутативність). (комутативність).
2. (α  )· )·  =α ( =α (  · ·  ) (скаляр. множник можна винос. за знак скаляр. добутку). ) (скаляр. множник можна винос. за знак скаляр. добутку).
3. (  + +  )· )·  = =  · ·  + +  · ·  (дистрибутивність). (дистрибутивність).
Доведення.
1. Властивість випливає з означення скалярного добутку.
2. Нехай в ортонормов. базисі вектори  і і  мають координати мають координати  = (а1, а2, а3), = (а1, а2, а3),  = (b1, b2, b3). Тоді за наслід8 вектор α· = (b1, b2, b3). Тоді за наслід8 вектор α·  = (α а1, α а2, α а3) і за теор8 = (α а1, α а2, α а3) і за теор8
(α  )· )·  = α а1b1+α а2 b2+α а3 b3 = α (а1b1+а2 b2+а3 b3 ) = α ( = α а1b1+α а2 b2+α а3 b3 = α (а1b1+а2 b2+а3 b3 ) = α (  · ·  ). ).
3. Нехай в ортонормованому базисі вектори  , ,  і і  мають координати: мають координати:  = (а1, а2, а3), = (а1, а2, а3),  = (b1, b2, b3), = (b1, b2, b3),  =(c1, c2, c3 ). За наслід6 вектор =(c1, c2, c3 ). За наслід6 вектор  + +  = (а1 +b1 , а2 +b2 , а3 +b3 ) і ( = (а1 +b1 , а2 +b2 , а3 +b3 ) і (  + +  ) · ) ·  = (а1 +b1 ) c1 +(а2 +b2 ) c2 +(а3 +b3 ) c3 = = (а1 +b1 ) c1 +(а2 +b2 ) c2 +(а3 +b3 ) c3 =
= (а1 c1 +а2 c2 +а3 c3 ) + (b1 c1 +b2 c2 +b3 c3 ) =  · · 
2. Векторний та мішаний добутки векторів, їх властивості та застосування.
Векторним добутком двох векторів  та та  наз. вектор наз. вектор  , для якого виконуються умови: 1. | , для якого виконуються умови: 1. |  | дорівнює площі паралелограма побудованого на векторах | дорівнює площі паралелограма побудованого на векторах  і і  . (| . (|  |=| |=|  || ||  | sin( | sin(  ˆ ˆ  ) ). 2. ) ). 2.  перпендикулярний як з перпендикулярний як з  так і з так і з  . 3. Якщо . 3. Якщо  та та  не колінеарні, то вектор не колінеарні, то вектор  має такий напрямок, що впорядкована трійка векторів має такий напрямок, що впорядкована трійка векторів  , ,  , ,  має праву орієнтацію (рис. 16). має праву орієнтацію (рис. 16).
Векторний добуток позначають  =[ =[  , ,  ] або ] або  = =  × ×  . .
З означ. слідує: якщо вектори колінеарні, то їх векторний добуток рівний нулю.
Теор10.Для того, щоб вектори були колінеарними необхідно і досить, щоб їх векторний добуток дорівнював нулю.
Властивості:
1. [  , ,  ]= - [ ]= - [  , ,  ] (антикомутативність). ] (антикомутативність).
2.α [  , ,  ]=[α ]=[α  , ,  ]=[ ]=[  ,α ,α  ](винесення скалярного множника). ](винесення скалярного множника).
3.[  , ,  + +  ]=[ ]=[  , ,  ]+[ ]+[  , ,  ], [ ], [  + +  , ,  ]=[ ]=[  , ,  ]+[ ]+[  , ,  ] (дистрибутивність). ] (дистрибутивність).
Доведемо перші дві властивості.
1. Якщо вектори  і і  колінеарні, то [ колінеарні, то [  , ,  ] = [ ] = [  , ,  ] =0 і властив. доведена. Нехай ] =0 і властив. доведена. Нехай  та та  неколінеарні. Тоді вектори [ неколінеарні. Тоді вектори [  , ,  ] і [ ] і [  , ,  ]мають однакові модулі, але протилежно направлені, оскільки трійки векторів ]мають однакові модулі, але протилежно направлені, оскільки трійки векторів  , ,  ,[ ,[  , ,  ] і ] і  , ,  [ [  , ,  ] мають протилежну орієнтацію. Це означає, що [ ] мають протилежну орієнтацію. Це означає, що [  , ,  ]= -[ ]= -[  , ,  ]. ].
2. Доведемо першу рівність. Якщо α=0, то рівність очевидна. Нехай α> 0. Тоді |[α  , ,  ]| = |α ]| = |α  || ||  | sin(α | sin(α  ˆ ˆ  ) = α | ) = α |  || ||  | sin( | sin(  ˆ ˆ  ) = =|α[ ) = =|α[  , ,  ]|. Оскільки α> 0, то очевидно, що вектори α[ ]|. Оскільки α> 0, то очевидно, що вектори α[  , ,  ]і [α ]і [α  , ,  ]співнаправлені. Якщо α< 0, то як і раніше можна показати, що |[α ]співнаправлені. Якщо α< 0, то як і раніше можна показати, що |[α  , ,  ]|=|α[ ]|=|α[  , ,  ]|. А напрямок вектора [α ]|. А напрямок вектора [α  , ,  ]протилежний до напрямку [ ]протилежний до напрямку [  , ,  ], але такий же як вектора α[ ], але такий же як вектора α[  , ,  ]. Отже, α[ ]. Отже, α[  , ,  ]=[α ]=[α  , ,  ]. Аналогічно доводиться друга рівність. ]. Аналогічно доводиться друга рівність.
Теор11.Якщо вектори  та та  в с-мі коор. (O, в с-мі коор. (O,  , ,  , ,  ) мають відповідно координати ) мають відповідно координати  =(a1,a2,a3), =(a1,a2,a3),  =(b1,b2,b3), то їх векторний добуток знаходиться за формулою:[ =(b1,b2,b3), то їх векторний добуток знаходиться за формулою:[  , ,  ]= ]=  (21) (21)
Доведення. Запиш. розклади даних векторів по базису:  = a1 = a1  +a2 +a2  +a3 +a3  , ,  =b1 =b1  +b2 +b2  +b3 +b3  . Тоді, користуючись властивостями, отримаємо: . Тоді, користуючись властивостями, отримаємо:
[  , ,  ]=[a1 ]=[a1  +a2 +a2  +a3 +a3  , b1 , b1  +b2 +b2  +b3 +b3  ]= ]=
= a1b2[  , ,  ]+a1b3[ ]+a1b3[  , ,  ]+a2b1[ ]+a2b1[  , ,  ]+a2b3[ ]+a2b3[  , ,  ]+a3b1[ ]+a3b1[  , ,  ]+a3b2[ ]+a3b2[  , ,  ]. Так як [ ]. Так як [  , ,  ]= ]=  , [ , [  , ,  ] = ] =  , [ , [  , ,  ] = ] =  , то отримаємо [ , то отримаємо [  , ,  ]=(a2b3 - -a3b2) ]=(a2b3 - -a3b2)  +(a3b1 - a1b3) +(a3b1 - a1b3)  +(a1b2 - a2b1 ) +(a1b2 - a2b1 )  = =   + + 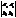  + +   . .
Мішаним добутком векторів  , ,  і і  (позначається ( (позначається (  , ,  , ,  )) наз. скалярний добуток вектора )) наз. скалярний добуток вектора  на векторний добуток векторів на векторний добуток векторів  та та  : :
 [ [  , ,  ]=( ]=(  , ,  , ,  )=[ )=[  , ,  ] ]  . .
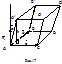 Теор12 (Геометричний зміст мішаного добутку). Теор12 (Геометричний зміст мішаного добутку).
Якщо вектори  , ,  , ,  не компланарні, то модуль мішаного добутку |( не компланарні, то модуль мішаного добутку |(  , ,  , ,  )| дорівнює об’єму паралелепіпеда побудованого на векторах )| дорівнює об’єму паралелепіпеда побудованого на векторах  , ,  , ,  (рис.17). (рис.17).
Доведення:
Розглянемо векторний добуток [  , ,  ]. Позначимо ]. Позначимо  одиничний вектор, співнаправлений з [ одиничний вектор, співнаправлений з [  , ,  ], а φ – кут між ним і вектором ], а φ – кут між ним і вектором  . Враховуючи, що [ . Враховуючи, що [  , ,  ]=|[ ]=|[  , ,  ]| ∙ ]| ∙  = SOBDC = SOBDC  , отримаємо: ( , отримаємо: (  , ,  , ,  ) = ) =  ∙[ ∙[  , ,  ] = ] =  ∙ SOBDC ∙ SOBDC  = SOBDC = SOBDC  ∙ ∙  = SOBDC | = SOBDC |  || ||  | cosφ == SOBDC (+/- h) = +/- V (оскільки вектори | cosφ == SOBDC (+/- h) = +/- V (оскільки вектори  і і  можуть утворювати як гострий кут (рис.17) так і тупий (вектор можуть утворювати як гострий кут (рис.17) так і тупий (вектор  направлений вниз), то cosφ може бути як додатній, так і від’ємний). Отже V=|( направлений вниз), то cosφ може бути як додатній, так і від’ємний). Отже V=|(  , ,  , ,  )|. Теорему доведено. )|. Теорему доведено.
Теор13.Якщо вектори  , ,  та та  мають координати мають координати  =(a1,a2,a3), =(a1,a2,a3),  =(b1,b2,b3), =(b1,b2,b3),  =(с1,с2,с3) то мішаний добуток цих векторів дорівнює визначнику 3-го порядку, складному з їх координат: ( =(с1,с2,с3) то мішаний добуток цих векторів дорівнює визначнику 3-го порядку, складному з їх координат: (  , ,  , ,  )= )= 
Доведення: Знайдемо векторний добуток векторів  і і  . Згідно формули (21): ∙[ . Згідно формули (21): ∙[  , ,  ] = ] =  . Тоді . Тоді
(  , ,  , ,  ) = ) =  [ [  , ,  ]= а1 ]= а1 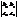 +а2 +а2  + а3 + а3  = = 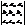 . .
Мішаний добуток векторів рівний визначнику третього порядку, а значить має такі ж властивості, як і визначники.
Властивості:
1. Якщо три вектори компланарні то мішаний добуток дорівнює нулю.
2. Мішаний добуток додатній, якщо впорядкована трійка векторів  , ,  , ,  має додатну орієнтацію і навпаки. має додатну орієнтацію і навпаки.
3. При перестановці місцями двох векторів у мішаному добутку, знак визначника змінюється на протилежний, а його абсолютна величина не змінюється: 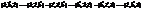 . .
4. Число можна виносити за знак мішаного добутку:
α (  , ,  , ,  )=(α )=(α  , ,  , ,  )=( )=(  ,α ,α  , ,  )=( )=(  , ,  ,α ,α  ). ).
5. Якщо один з векторів являється сумою інших, то:
|


 =
=  і
і  =
=  наз. вектор
наз. вектор  =
=  , який є діагоналлю паралелограма, побудов. на векторах
, який є діагоналлю паралелограма, побудов. на векторах  . Так як
. Так як  =
=  +
+ 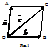 Правило додавання векторів, яке визначається цією формулою, називається правилом трикутника.
Правило додавання векторів, яке визначається цією формулою, називається правилом трикутника. 1. Для будь-яких векторів
1. Для будь-яких векторів  +
+ 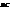 )=
)=  вектор , такий, що для будь-якого
вектор , такий, що для будь-якого  , так як
, так як  +
+  +
+  .
. ; тоді
; тоді  =
=  =
=  наз. такий вектор
наз. такий вектор  , що
, що  +
+  =
=  Різниця будь-яких векторів
Різниця будь-яких векторів  –
–  =
=  =
=  =
=  =
=  2.α·(
2.α·(  =
=  (рис.4).
(рис.4).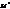 +
+  =
=  C
C  =
=  ,
,  ,
,  , де
, де 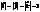 і всі кути між цими векторами рівні 900
і всі кути між цими векторами рівні 900  (4)
(4) =
= 
 .
. =
=  і
і  . (|
. (|  (21)
(21) +(a1b2 - a2b1 )
+(a1b2 - a2b1 ) 

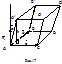 Теор12 (Геометричний зміст мішаного добутку).
Теор12 (Геометричний зміст мішаного добутку). одиничний вектор, співнаправлений з [
одиничний вектор, співнаправлений з [  = SOBDC
= SOBDC 
 . Згідно формули (21): ∙[
. Згідно формули (21): ∙[  . Тоді
. Тоді +а2
+а2  + а3
+ а3  =
=  .
. .
.