
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Пример составление уравнений по законам Кирхгофа для расчета электрических цепей.В представленной цепи на рис. 3.12 известны e1(t), e3(t) и все элементы Rk, xLk и xCk.
Рис. 3.12
Необходимо определить токи i1(t), i2(t), i3(t). Условно положительные направления токов выбраны произвольно. Такая цепь может быть рассчитана только в символической форме. Аналог этой цепи в комплексной версии представлен на рис. 3.13.
Рис. 3.13
Расчет будем вести по действующим значениям. В случае, если:
и
комплексное действующее значение этих ЭДС равны:
Комплексное полное (кажущиеся) сопротивления ветвей при этом равны:
При этом
В рассматриваемой схеме два узла, три ветви и два ячеечных контура. Это означает, что в схеме три неизвестных тока и для ее расчета необходимо составить (по законам Кирхгофа) три независимых уравнения. По первому закону составляется одно уравнение, например для узла 1:
Ясно, что второе уравнение (для узла 2): Два недостающих уравнения составляются для двух ячеечных контуров: I: II: Обход каждого контура выбран по часовой стрелке. Падения напряжения на каждом сопротивлении совпадает с направлением соответствующего тока и по закону Ома равны:
При составлении уравнений ЭДС, совпадающим с обходом контура, приписывается знак «плюс» ( Таким же образом приписываются знаки падения напряжений. В результате решения составленной системы уравнений получаем Как уже было отмечено, расчет сложных электрических цепей по законам Кирхгофа не является оптимальным, однако эти законы незаменимы, например, при построении векторных диаграмм, определении падений напряжений между любыми двумя точками цепи, при всех видах анализа изменяющихся режимов и т.п.  Например, после расчета цепи (см. рис. 3.13) возникла необходимость определить напряжение между точками А и В, это легко делается по второму закону Кирхгофа. Для этого необходимо произвольно выбрать направление падения напряжения На рис. 3.13 показаны два таких контура – M и N (пунктирные линии обхода). Для контура М (
Для контура N (при обходе его по часовой стрелке), включающего в себя
т.е.
Метод контурных токов
Метод контурных токов является следствием законов Кирхгофа и метода (принципа) наложения. Фактически – это второй закон Кирхгофа для контуров электрической цепи, чаще всего – для ячеечных контуров. Правило составления уравнений по методу контурных токов легко определяется путем исключения из уравнений второго закона Кирхгофа для ячеечных контуров любой электрической цепи токов внутренних ветвей этой цепи, что легко сделать с использованием уравнений, составленных для нее по первому закону. Суть этого правила состоит в следующем. Условно считают, что во всех ветвях каждого ячеечного контура имеет место один и тот же ток – контурный ток этого контура (рис. 3.14).
Рис. 3.14 Направление контурных токов в каждом контуре выбирается по направлению обхода контура при составлении уравнений по второму закону, т.е. (как правило) – по часовой стрелке. Возникающее при этом очевидное недоразумение (один ток в разных ветвях) легко снимается принципом положения: – в каждой внешней ветви в этом случае имеет место только один ток – контурный ток (см. рис. 3.14), создающий падение напряжения на всех элементах внешней ветви (закон Ома); – в каждой внутренней ветви в этом случае имеют место два контурных тока соседних контуров, при выбранных нами направлениях (либо все токи по часовой стрелке, либо все – против) всегда направленных навстречу друг другу. Каждый контурный ток внутренней ветви на всех ее элементах создает собственное падение напряжения. Значит, в каждом элементе внутренней ветви имеют место два напряжения: одно – от контурного тока рассматриваемого контура, следовательно, совпадающее с направлением обхода, а другое – от направленного в противоположную сторону тока соседнего контура, т.е. направленного навстречу обходу. На основе принципа (метода) наложения контурных токов в ветвях каждого ячеечного контура, закона Ома и второго закона Кирхгофа получаем правило составления уравнений по методу контурных токов для контуров цепи. Для цепи, представленной на рис. 3.14 имеем: Первый контур.
Второй контур.
Третий контур.
Таким образом, концепция существования виртуальных контурных токов позволяет существенно сократить количество составляемых для расчета цепи уравнений, и теоретически вполне оправдана. Если в каждом k-том ячеечном контуре с контурным током
Положительным в правой части этих уравнений будет только одно слагаемое типа В этой связи система уравнений для цепи (рис. 3.14) может быть представлена в виде:
Положительные слагаемые справа здесь располагаются по диагонали. Такая система для трех (для любого количества) контуров может быть составлена не глядя на схему, которая потребуется только для определения значений ЭДС Такая система легко может быть переведена в матричную форму и решена с использованием компьютерных технологий. Иногда сумму сопротивлений ветвей каждого k-того контура zkk называют (что не вполне корректно) собственным сопротивлением контура. Предельно просто такая схема решается с помощью определителей. Реальные токи в ветвях находятся на основе принципа наложения (или первого закона Кирхгофа), в соответствии с которым реальные токи во внешних ветвях (там только один ток) равны контурным токам соответствующих контуров и совпадают с ними по направлению. В нашем примере Рекомендуется из тока с большим модулем (величиной) его комплексного изображения вычитать ток с меньшим модулем с сохранением направления первого. При указанных направлениях реальных токов
что означает
В цепях синусоидального тока это правило принципиального значения не имеет, поскольку знак перед синусом переносится в его начальную фазу, а в цепях постоянного тока это исключает получение отрицательных значений реальных токов. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 475. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


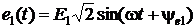
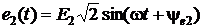 ,
,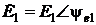 ,
,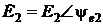 .
. ,
, ,
, .
.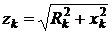 ,
, .
. .
. смысла не имеет, повторяя первое уравнение.
смысла не имеет, повторяя первое уравнение. ;
;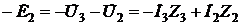 .
. .
. ), а не совпадающим – знак «минус» (
), а не совпадающим – знак «минус» (  ).
). , по которым легко устанавливаются i1(t), i2(t) и i3(t).
, по которым легко устанавливаются i1(t), i2(t) и i3(t). и составить уравнение для любого замкнутого контура, включающего ветви с известными токами и напряжение
и составить уравнение для любого замкнутого контура, включающего ветви с известными токами и напряжение  ) получаем:
) получаем: .
. уравнение имеет вид:
уравнение имеет вид: ,
, .
.
 .
. .
. .
. алгебраическую сумму ЭДС обозначить
алгебраическую сумму ЭДС обозначить  , сумму сопротивлений ветвей этого контура обозначить zkk, а сопротивление каждой из ветвей, смежных между контурами «k» и «m» обозначить zkm, уравнение по методу контурных токов для любого k-того контура представляется, как:
, сумму сопротивлений ветвей этого контура обозначить zkk, а сопротивление каждой из ветвей, смежных между контурами «k» и «m» обозначить zkm, уравнение по методу контурных токов для любого k-того контура представляется, как: .
. , все остальные – отрицательны.
, все остальные – отрицательны.
 ,
, 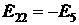 и
и  ) и сопротивлений zkk и zkm (у нас z11= z1 + z6 + z2, z12= z21= z2, z13= z31= z3, z22= z2 + z6 + z5, z23= z32= z6, z33= z3 + z4 + z6).
) и сопротивлений zkk и zkm (у нас z11= z1 + z6 + z2, z12= z21= z2, z13= z31= z3, z22= z2 + z6 + z5, z23= z32= z6, z33= z3 + z4 + z6).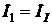 ,
,  и
и  . Реальные токи в смежных между двумя ячеечными контурами ветвях находятся наложением друг на друга двух направленных в противоположные стороны токов смежных контуров.
. Реальные токи в смежных между двумя ячеечными контурами ветвях находятся наложением друг на друга двух направленных в противоположные стороны токов смежных контуров. ,
,  и
и  во внутренних ветвях цепи на рис. 3.14 они получены следующим образом:
во внутренних ветвях цепи на рис. 3.14 они получены следующим образом: ,
, ,
,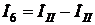 ,
, ,
, ,
,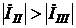 .
.