
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Часть IV. Резонансы и магнитные связи в электрических цепях
Рассмотренные в первых трех частях пособия физические основы и общая теория электрических цепей является фундаментом как для понимания принципов функционирования линейных электрических цепей или электротехнических устройств любой конфигурации и назначения, так и для формирования частной теории, учитывающей специфику их работы. В рамках теоретических основ электротехники отдельно рассматриваются, например, теория трехфазных электрических цепей, теория четырехполосников, теория линий с распределенными параметрами и т.п. Однако, в основе каждой из них лежат рассмотренные общие физические основы и принципы электромагнитных процессов в элементах этих цепей и цепях в целом, формируемые законами Джоуля-Ленца, Фарадея, Ампера, Ома и Кирхгофа и обусловленные этими законами методы расчетов (эквивалентных преобразований, контурных токов, узловых потенциалов и др). Осознанное понимание общей теории и приобретенная способность ее практического использования позволяют сравнительно легко при необходимости самостоятельно освоить любую частную теорию цепей, систем и устройств. В качестве примера далее рассматриваются два имеющих чрезвычайно важное практическое значение в электроэнергетике и электротехнике раздела ТОЭ - резонансные явления и магнитные связи в электрических цепях. Резонансные явления в электрических цепях Общие положения Любой приемник электрической энергии, как известно, всегда может быть представлен в виде пассивного двухполюсника, в общем случае содержащего и активные сопротивления, и индуктивности, и емкости. Основными характеристиками, описывающими режим работы такого двухполюсника (Рис. 76), являются входное напряжение 
Рис. 76 Следствием этих характеристик, в значительной степени полно описывающих режим работы двухполюсника, являет фазовое соотношение между входными напряжением и током, т.е. сдвиг по фазе между ними:
Ранее детально были рассмотрены два возможных принципиально разных режима работы двухполюсника. Двухполюсник «носит» индуктивный характер. В этом случае Двухполюсник носит емкостный характер. В этом случае Это - основные в рамках электроэнергетики режимы работы приемников (цепи, в целом). Тем не менее довольно часто в электроэнергетических системах, а в системах радиосвязи и телекоммуникации повсеместно, приходится иметь дело с третьим режимом работы цепи, когда, несмотря на наличие в ней индуктивностей, и емкостей, со стороны входа она воспринимается как чисто активное сопротивление. Такой режим работы цепи и называется резонансным (смысл названия будет пояснен позднее). В этом случае:
Т.е. входные напряжение и ток по фазе совпадают (рис. 77)
Рис. 77 Условие Понятно, что в этом случае реактивная мощность на входе Как было отмечено ранее, любой пассивный двухполюсник с помощью эквивалентных преобразований всегда может быть приведен к двум эквивалентным схемам - последовательное и параллельное соединение идеальных Резонанс напряжений Резонанс напряжений имеет место в цепи с последовательным соединением
Рис. 78 При В нашем случае это условие имеет продолжение (см. Треугольники напряжений и сопротивлений), а именно Векторная диаграмма цепи с последовательным соединением R,
Рис. 79 в соответствии с тем, что
Рис. 80 Находящиеся в противофазе синусоиды в каждый момент времени компенсируют друг друга, резонируют (отсюда - резонанс). Важнейшим следствием резонанса является то, что питающая напряжение при резонансе равно напряжению на активном сопротивлении.
В некотором смысле можно считать, что связи с Из того, что - при неизменных L и С резонанс наступает при частоте - при неизменной частоте и индуктивности, резонанс досттгается при резонансной емкости - наконец, при Отношение при резонансе
При этом Величина Очень часто исследование резонанса напряжений сопровождается исследованием частотных характеристик, к которым относятся
Рис. 81 Ясно, что Что касается фазово-частотной характеристики Принципиальным является то, что при резонансе Зависимости действующих значений Наибольший интерес из них представляет зависимость
Рис. 82 При При При резонансной частоте ток становится максимальным, поскольку Резонанс токов Любая сложная электрическая цепь (или участок цепи) может быть приведена к эквивалентному параллельному соединению идеальных R, L и С (рис. 83). в этом случае удобнее оперировать не с сопротивлениями R,
Рис. 83. Логика и смысл дальнейших действий при исследовании резонанса токов полностью совпадает с действиями при исследовании резонанса напряжений и приводят к одному и тому же результату: Сдвиг по фазе между входным напряжением
Векторная диаграмма тока для этой цепи имеет вид рис. 84 с учетом того, что
Рис. 84 Ток в ветви с индуктивностью здесь находится ы противофазе с током в емкости, т.е. Добротность цепи в режиме резонанса равна Общий ток в такой цепи при резонансе равен току в ветви с активной проводимостью. Частотными в этом случае характеристиками цепи Легко видеть, что это - те же частотные характеристики, что и в случае последовательного соединения R, L, C, если сопротивления поменять на проводимости, индуктивности - на емкости, емкости - на индуктивности. Такие цепи называются дуальными. То же самое в дуальных цепях относится и к резонансным кривым, если параллельную цепь питать не от источника напряжения, а от источника тока, а питание напряжения на элементах поменять на токи в них. Итак, при резонансе токов резонируют тока, а точнее - реактивные составляющие токов При равенстве величин реактивных составляющих ветви с емкостью
Рис.
4.1.4. Проблема «Cos φ» Идея компенсации реактивной мощности, о которой и говорится при исследовании резонансов, имеет исключительно важное значение в электроэнергетических системах и сетях, как раз и позволяя решить проблему «Cos φ». Суть этой проблемы состоит в следующем. На рис. 86 представлена схема электрической цепи, в упрощенном виде моделирующая систему передачи электрической энергии от генератора (Г) к нагрузке (Н) по линии перелачи (Л).
Рис. 86 Здесь RЛ - активное сопротивление проводов линий (индуктивная и емкостная составляющие не рассматриваются), RH и хLH - параметры нагрузки. В связи с тем, что практически все виды нагрузок в электроэнергетических системах имеют индуктивный характер (двигатели, трансформаторы и т.п.), емкостными составляющими пренебрегают из-за их малости. В связи с этим векторная диаграмма на стороне нагрузки имеет вид рис. 87.
Рис. 87 Будем считать, что речь идет просто об электрическом двигателе. В паспорте любого двигателя указываются величины потребляемой двигателем в номинальном режиме работы номинальной мощности РН , номинального питающего напряжения В то же время затребованная потребителем соответствующая этому току мощность Это означает, что для выполнения требуемой потребителю работы, по идее, достаточно только активной составляющей тока Величина не участвующей в выполнении этой программы реактивной составляющей потребляемого общего тока (треугольник токов) равна
Реактивная составляющая тока формирует реактивную мощность Эта мощность «бесполезно» «курсирует» между генератором и нагрузкой, нагружая сеть и не выполняя какой-либо полезной работы. В этом и состоит проблема «Cos φ». Включение параллельно с индуктивной нагрузкой емкости при сохранении в двигателе
Рис. 88 В этом случае ток в линии и генераторе равен На практике при подборе емкости для компенсации реактивной мощности нагрузок полной компенсации резонанса стараются избегать, приводя работу цепи к околорезонансной. Это позволяет в связи с изменением параметров рабочего режима исключить вероятность возможной перекомпенсации при превышении реактивной составляющей емкостного тока реактивной составляющей тока нагрузки. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 553. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , входной ток
, входной ток 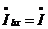 и входная (потребляемая) мощность
и входная (потребляемая) мощность

 (см. Треугольник мощностей).
(см. Треугольник мощностей).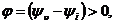
 ,
,  и ток отстает по фазе от напряжения.
и ток отстает по фазе от напряжения.
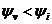 ,
,  и ток опережает по фазе напряжение.
и ток опережает по фазе напряжение.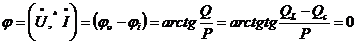 ,
,
 = 0, при наличии в цепи (участке цепи) индуктивностей и емкостей является основным для существования резонанса.
= 0, при наличии в цепи (участке цепи) индуктивностей и емкостей является основным для существования резонанса. , т.е.
, т.е.  и цепь от источника «потребляет» только активную мощность. При этом в индуктивных элементах двухполюсника имеет место индуктивная мощность
и цепь от источника «потребляет» только активную мощность. При этом в индуктивных элементах двухполюсника имеет место индуктивная мощность 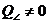 , а в емкостных - емкостная мощность
, а в емкостных - емкостная мощность 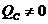 . Своеобразие режима состоит в том, что имеющие противоположные реактивные знаки мощности компенсируют друг друга. Поэтому режим резонанса часто называют режимом компенсации реактивной мощности.
. Своеобразие режима состоит в том, что имеющие противоположные реактивные знаки мощности компенсируют друг друга. Поэтому режим резонанса часто называют режимом компенсации реактивной мощности. . В связи с этим рассматриваются два типа резонансов.
. В связи с этим рассматриваются два типа резонансов.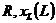 и
и  (рис. 78).
(рис. 78).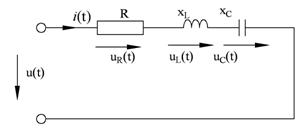
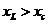 такая цепь имеет индуктивный характер, при
такая цепь имеет индуктивный характер, при 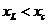 - емкостный. Естественно, в этой цепи может иметь место резонанс, основным условием которого является
- емкостный. Естественно, в этой цепи может иметь место резонанс, основным условием которого является  .
. . Это значит, что
. Это значит, что  и
и  , что в свою очередь приводит к необходимому и достаточному условию резонанса напряжений в цепи, т.е.
, что в свою очередь приводит к необходимому и достаточному условию резонанса напряжений в цепи, т.е.  и
и  . Кроме того, с учетом
. Кроме того, с учетом 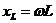 , а
, а  , получаем еще одно условие резонанса, а именно
, получаем еще одно условие резонанса, а именно  .
.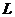 и С при резонансе представлена на рис. 79
и С при резонансе представлена на рис. 79
 и
и  синусоиды
синусоиды  и
и  в режиме резонанса находятся в противофазе, т.к.
в режиме резонанса находятся в противофазе, т.к.  , а
, а  , что и приводит к сдвигу по фазе между ними
, что и приводит к сдвигу по фазе между ними  (рис. 80).
(рис. 80).

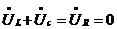 ; реактивное сопротивление в работе цепи в режиме резонанса не участвует. Это может привести к тому, что напряжение на индуктивности и емкости
; реактивное сопротивление в работе цепи в режиме резонанса не участвует. Это может привести к тому, что напряжение на индуктивности и емкости  и
и  при
при  оказывается больше питающего напряжения
оказывается больше питающего напряжения 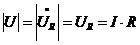 . В таком случае в цепи возникают перенапряжения, которые могут быть значительными и представлять опасность для работы цепи и обслуживающего персонала.
. В таком случае в цепи возникают перенапряжения, которые могут быть значительными и представлять опасность для работы цепи и обслуживающего персонала. следует, что резонансный режим может быть достигнут тремя путями:
следует, что резонансный режим может быть достигнут тремя путями: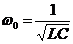 , называемый резонансной.
, называемый резонансной. ;
; и
и  , резонанс наступает при резонансной индуктивности
, резонанс наступает при резонансной индуктивности  .
. к
к  , т.е.
, т.е. называется добротностью контура с последовательным соединением R, L, C, а величина, обратная добротности
называется добротностью контура с последовательным соединением R, L, C, а величина, обратная добротности  - называется затуханием.
- называется затуханием. и
и  .
. имеющая размерность сопротивления называется волновым сопротивлением
имеющая размерность сопротивления называется волновым сопротивлением  контура.
контура. и
и  . Соответствующие кривые приведены на рис. 81.
. Соответствующие кривые приведены на рис. 81.
 от частоты не зависит,
от частоты не зависит,  - прямо пропорционально частоте,
- прямо пропорционально частоте, 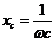 - обратно пропорционально частоте,
- обратно пропорционально частоте,  строится простым алгебраическим сложением (вычитанием) двух функций, а
строится простым алгебраическим сложением (вычитанием) двух функций, а  легко строится по
легко строится по  и
и  .
. она плавно изменяется от
она плавно изменяется от  до
до  , изменяя свой знак при
, изменяя свой знак при  в связи с тем, что здесь х изменяет свой знак от
в связи с тем, что здесь х изменяет свой знак от  .
. является минимальной величиной, равной активному сопротивлению.
является минимальной величиной, равной активному сопротивлению. при
при  называются резонансными кривыми.
называются резонансными кривыми.
 , представленная на рис. 82.
, представленная на рис. 82.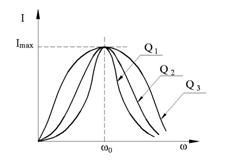
 (постоянное напряжение) ток равен нулю, т.к. конденсатор на постоянном токе - разрыв цепи.
(постоянное напряжение) ток равен нулю, т.к. конденсатор на постоянном токе - разрыв цепи. ток устремляется к нулю, т.к. сопротивление индуктивности при
ток устремляется к нулю, т.к. сопротивление индуктивности при  есть разрыв цепи, т.е.
есть разрыв цепи, т.е.  .
. минимально. При этом форма кривой
минимально. При этом форма кривой  существенно зависит от добротности и, чем меньше она, тем более «раздутой» оказывается колокольная форма кривой тока. На рис. 82
существенно зависит от добротности и, чем меньше она, тем более «раздутой» оказывается колокольная форма кривой тока. На рис. 82  . Такая зависимость
. Такая зависимость  и
и  , индуктивный
, индуктивный  и емкостный
и емкостный  . Полная (кажущаяся) проводимость в этом случае равна
. Полная (кажущаяся) проводимость в этом случае равна  .
.
 .
. и входным током
и входным током  в параллельной цепи, как известно, равен
в параллельной цепи, как известно, равен  , что следует из треугольников действующих значений токов и проводимостей и означает, что
, что следует из треугольников действующих значений токов и проводимостей и означает, что  и
и  , что в свою очередь приводит к необходимому и достаточному условию резонанса токов в цепи, т.е.
, что в свою очередь приводит к необходимому и достаточному условию резонанса токов в цепи, т.е.  или
или  и
и  , а с учетом зависимостей
, а с учетом зависимостей  и
и  к общему для резонансов условию:
к общему для резонансов условию:
 и
и  ,
,  и
и  . Понятно, что
. Понятно, что  и входные ток и напряжение по фазе совпадают.
и входные ток и напряжение по фазе совпадают.
 и компенсируют друг друга (резонируют). Резонирующий контур «L-C» не нуждается в поступлении энергии от источника, представляет из себя идеальный колебательный контур, детально исследованный в курсе физики.
и компенсируют друг друга (резонируют). Резонирующий контур «L-C» не нуждается в поступлении энергии от источника, представляет из себя идеальный колебательный контур, детально исследованный в курсе физики. =
=  , затухание
, затухание  , а волновая проводимость
, а волновая проводимость  .
. ,
,  ,
,  и
и  ,
,  ,
,  ,
,  ,
,  и
и  .
. в параллельных ветвях.
в параллельных ветвях.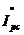 и ветви с индуктивностью
и ветви с индуктивностью  (рис. _____) т.е. при
(рис. _____) т.е. при 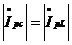 любой из токов ветви с емкостью (
любой из токов ветви с емкостью (  и др.) будет резонировать с любым из током (
и др.) будет резонировать с любым из током (  и др.) ветви с индуктивностью.
и др.) ветви с индуктивностью.

 , номинального коэффициента мощности
, номинального коэффициента мощности  и номинального тока
и номинального тока  . Именно при этом режиме работа двигателя оказывается наиболее эффективной. Потребляемый при этом двигателем ток
. Именно при этом режиме работа двигателя оказывается наиболее эффективной. Потребляемый при этом двигателем ток  вырабатывается генератором и по линии передачи поставляется потребителю, нагружая этим током генератор и нагревая провода линии через сопротивление RЛ и удаляя электрическую энергию в окружающее пространство (потери). Работать эффективно при другом токе двигатель просто не может..
вырабатывается генератором и по линии передачи поставляется потребителю, нагружая этим током генератор и нагревая провода линии через сопротивление RЛ и удаляя электрическую энергию в окружающее пространство (потери). Работать эффективно при другом токе двигатель просто не может..
 . Например, номинальная мощность асинхронного двигателя А2-91-4 равна РН = 75 квт, при
. Например, номинальная мощность асинхронного двигателя А2-91-4 равна РН = 75 квт, при  ,
,  В и
В и  . Генератор при этом нагружается током 193 А, провода линии электропередачи греются именно этим током
. Генератор при этом нагружается током 193 А, провода линии электропередачи греются именно этим током  при том, что для выполнения производственной программы достаточно было бы получить от генератора только
при том, что для выполнения производственной программы достаточно было бы получить от генератора только  А.
А. А
А (треугольник мощностей) = 38,4 ВА.
(треугольник мощностей) = 38,4 ВА. и сos φН позволяет существенно уменьшить ток в линии IЛ и следовательно, ток в генераторе
и сos φН позволяет существенно уменьшить ток в линии IЛ и следовательно, ток в генераторе 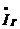 вплоть до полной компенсации реактивной составляющей тока и реактивной мощности в сети при резонансе. Схема такой цепи и векторная диаграмма для случая резонанса представлены на рис. 88 (а, b)
вплоть до полной компенсации реактивной составляющей тока и реактивной мощности в сети при резонансе. Схема такой цепи и векторная диаграмма для случая резонанса представлены на рис. 88 (а, b)
 - только активному току нагрузки. Реактивная индуктивная мощность нагрузки, оставаясь прежней, шунтируется емкостью с непрерывным колебанием
- только активному току нагрузки. Реактивная индуктивная мощность нагрузки, оставаясь прежней, шунтируется емкостью с непрерывным колебанием  и
и  в замкнутом контуре
в замкнутом контуре  , освобождая генератор.
, освобождая генератор.