
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Идеальная катушка индуктивности в цепях синусоидального тока
Здесь речь идет о катушке индуктивности, не обладающей ни активным сопротивлением, ни емкостью (в реальной ситуации ими пренебрегают из-за их малости). В электрических схемах такие катушки представляются рис. 2.12.
Рис. .2.12
Взаимосвязь между напряжением u(t) и током i(t) в такой катушке определяется законом Фарадея, т.е.:
и
В случае синусоидальной формы напряжения
Это означает, что: 1. При синусоидальном напряжении на зажимах катушки ток в ней оказывается синусоидальным, т.е. 2. Амплитуда тока Im связана с амплитудой напряжения формулой внешне совпадающей с законом Ома, т.е.:
Понятно, что эти формулы справедливы и для действующих значений. 3. Совпадение этих формул с законом Ома усиливается, если учесть, что размерность величины wL имеет размерность сопротивления [1/сек×Гн = Ом]. Эта величина с физической точки зрения, не являясь сопротивлением, названа, тем не менее, сопротивлением с обязательным сопровождением «реактивное индуктивное», обозначаемое хL = wL = 2pfL [Ом]. Здесь и далее х – малая, прописная буква «икс». Ясно, что на постоянном токе (напряжении) при w = 0 и f = 0 индуктивное сопротивление катушки равно нулю. Участок с индуктивностью в этом случае представляет собой простой проводник без какого-либо сопротивления, т.е. короткое замыкание. Поэтому при расчете цепей постоянного тока индуктивность не рассматривается. И только в случае, когда ток начинает изменяться, в соответствии с Фарадеем в катушке индуктивности возникает ЭДС самоиндукции  Величина, обратная реактивному сопротивлению bL = 1/хL [1/Ом = См], называется реактивной индуктивной проводимостью катушки. 4. Частота тока совпадает с частотой питающего напряжения. 5. Сдвиг по фазе между напряжением и током равен j = yu – yi = 90°, т.е. ток в идеальной катушке индуктивности отстает по фазе от напряжения на 90° (p/2), что является признаком индуктивности. Полученные зависимости между амплитудами (действующими значениями), частотами и начальными фазами в соответствии с п.п. 1, 2, 3, 4 позволяют легко рассчитывать цепь (участок цепи) с идеальной индуктивностью, не прибегая к интегрированию или дифференцированию:
и
Если цепь с идеальной индуктивностью перенести в область комплексных изображений, реальные синусоиды напряжения и тока переводятся в их комплексные амплитуды или действующие значения:
и
В соответствии с правилами математических действий над оригиналами и их комплексными изображениями связь между током в индуктивности i(t) и напряжением на ее зажимах uL(t), а именно:
превращается в обычную алгебраическую зависимость:
Здесь xL = wL – полученное ранее значение индуктивного реактивного сопротивления катушки. Множитель XL = jxL является комплексным сопротивлением катушки. Здесь и далее Х – большая, заглавная буква «икс». Выражение Таким образом, при
где yi = yu – 90°. Этому комплексному действующему значению тока соответствует синусоида Векторная диаграмма катушки индуктивности на комплексной плоскости представлена на рис. 2.13,а.
а) b) Рис. 2.13
Комплексное изображение идеальной катушки представлено на рис. 2.13,b, это означает, что идеальная индуктивность в области оригиналов х2 = wL в области комплексных изображений представляется как
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 786. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


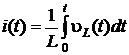 .
. имеем:
имеем:
 и задача сводится к определению Im, w и yi.
и задача сводится к определению Im, w и yi. или
или  .
.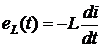 , препятствующая изменению тока, т.е. ведущая себя как сопротивление. Именно поэтому величина хL = wL , являющаясямерой ЭДС индукции и учитывающая реакцию катушки на изменение тока и называется реактивным сопротивлением. При неизменной частоте (установившийся ток) f = const сопротивление хL = const, но изменяется при изменении f.
, препятствующая изменению тока, т.е. ведущая себя как сопротивление. Именно поэтому величина хL = wL , являющаясямерой ЭДС индукции и учитывающая реакцию катушки на изменение тока и называется реактивным сопротивлением. При неизменной частоте (установившийся ток) f = const сопротивление хL = const, но изменяется при изменении f.
 .
.
 .
. ,
, .
. , как и в случае резистора внешне полностью совпадает с законом Ома и часто называется законом Ома для катушки индуктивности в комплексной форме.
, как и в случае резистора внешне полностью совпадает с законом Ома и часто называется законом Ома для катушки индуктивности в комплексной форме. и комплексном реактивном индуктивном сопротивлении
и комплексном реактивном индуктивном сопротивлении  комплексное действующее значение тока:
комплексное действующее значение тока: ,
, , при j = yu – yi = 90°. Ток отстает по фазе от напряжения на угол 90° (p/2).
, при j = yu – yi = 90°. Ток отстает по фазе от напряжения на угол 90° (p/2).

 .
.