
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Обобщенный приемник электрической энергии в цепях синусоидального тока
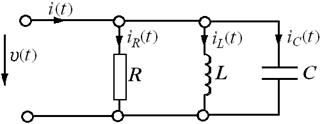
Как уже было отмечено, любой приемник электрической энергии, независимо от его конструктивного исполнения и назначения, с точки зрения теории электрических цепей всегда может быть представлен электрической моделью в виде того или иного набора идеальных R, L и С, в конечном счете – в виде эквивалентного пассивного двухполюсника с последовательным или параллельным соединением этих элементов. В этом смысле последовательные или параллельные соединения R, L и С можно считать обобщенным приемником электрической энергии. Последовательные соединения R, L и С. Электрическая схема такого приемника представлена на рис. 2.16.
Рис. 2.16
Понятно, что u(t) = uR(t) +uL(t) + uC(t). При этом uR(t) = i(t) × R,
Это означает, что при синусоидальном питающем напряжении, ток в цепи и напряжения на всех ее элементах – синусоиды одной и той же частоты. Если рассматриваемую цепь перевести в область комплексных изображений, получим цепь, представленную на рис. 2.17.
Рис. 2.17
Понятно, что в этой цепи:
и
а В соответствии с тем, что сложению синусоид uR(t), uL(t), uC(t) соответствует сложению их комплексных изображений, с учетом второго закона Кирхгофа и закона Ома в комплексной форме получаем:
Здесь Перевод показательной формы записи Z в алгебраическую форму приводит к тому, что: – модуль (величина) комплексного полного сопротивления Z равен  – аргумент Z, т.е. угол Величину z называют кажущимся сопротивлением потому, что в его составе наряду с сопротивлением R входит величина х, только условно называемая сопротивлением. Таким образом, связь между комплексными действующими значениями (или амплитудами) напряжения и тока обобщенного приемника электрической энергии внешне совпадает с законом Ома, что позволяет выражения Учитывая, что при:
а при:
получаем:
Это значит, что – если xu > xi , что соответствует тому, что j > 0 и xL > 0, в цепи преобладает индуктивность; – если xu < xi , т.е. j < 0, значит x < 0, т.е. в цепи преобладает емкость. В области оригиналов связь между действующими значениями (величинами) напряжения U и тока I или амплитудами Um и Im определяется подобием закона Ома, т.е. Это позволяет рассчитывать обобщенный приемник без использования комплексных изображений. Легко видеть, что все полученные зависимости для расчета последовательного соединения R, L и С являются общими и применимыми для расчета каждого из этих элементов в отдельности, поскольку при идеальном активном сопротивлении, когда хL= 0 и хС = 0 сопротивление Алгоритм расчета обобщенного приемника без использования комплексных изображений состоит в следующем: 1. При известном синусоидальном напряжении Значит, целью расчета является определение Im, w и yi. 2. 3. 4. 5. Частота тока равна частоте напряжения w. 6. Понятно, что рассчитывать такую цепь символическим методом нецелесообразно. Падения напряжений на каждом (идеальном) элементе приемника определяются по изложенным правилам расчета каждого из них в отдельности по найденному току в них. Например, при определении напряжения на индуктивности (оно будет синусоидальным)
При определении
При определении
При построении векторной диаграммы в связи с этим комплексную плоскость использовать не обязательно. Для этого один из векторов синусоидальных величин следует принять за основной (опорный) и на чертеже располагать его произвольно. Остальные векторы строить относительно опорного вектора с учетом сдвигов фаз между ними. Поскольку в рассматриваемом случае в каждом элементе имеет место один и тот же ток, именно его вектор и следует принять за опорный, а далее исходить из того, что источник напряжения на R совпадает с током по фазе, падение напряжения на L опережает ток на 90°, а на емкости С – отстает на 90° (рис. 2.18).
Рис. 2.18
Векторная диаграмм строится на основе второго закона Кирхгофа При построении векторной диаграммы (см. рис. 2.18) произвольно принято, что Если хL < хС , т.е. В случае, если хL = хС , окажется, что Проекция вектора напряжения на ток, т.е. При этом треугольник, составленный из величин напряжений (модулей соответствующих комплексных чисел), т.е.
Рис. 2.19
Из этого треугольника легко получить формулы связи, которые могут оказаться полезными при расчетах. Например, Если величины сторон этого треугольника разделить на величину действующего значения тока с учетом того, что
Рис. 2.20
Из этого треугольника легко получаются ранее полученные зависимости Параллельное соединение R, L и С. Схема такой цепи представлена на рис. 2.21. Понятно, что в этой цепи i(t) = iR(t) + iL(t) + iC(t).
Рис. 2.21
Для идеальных R, L и С:
при том, что i (t) = iR(t) + iL(t) + iC(t). Окончательное уравнение электрического состояния принимает вид:
При синусоидальном питающем напряжении:
токи во всех ветвях цепи будут синусоидальными с соответствующими комплексными действующими значениями Перевод исследуемой цепи в область комплексных изображений с учетом свойств оригиналов и изображений уравнение электрического состояния приводится к виду:
Таким образом, цепь, как и в случае последовательного соединения R, L, C, приводится к виду (рис. 2.22).
Рис. 2.22
Здесь Y – эквивалентная полная или кажущаяся проводимость цепи с учетом того, что 1/R = g – активная проводимость цепи, совпадающая с проводимостью ветви с R, b = –bL + bC – эквивалентная реактивная проводимость цепи при Таким образом, входной ток и входное напряжение связаны законом Ома в комплексной форме, т.е. Это значит, что если, например
Смена знака аргумента j, следовательно, знаков реактивных проводимостей b, bL и bC, может создать впечатление, что цепь в этом случае изменяет характер с индуктивного на емкостной (или наоборот). Конечно, этого не происходит. Характер цепи однозначно определяется ее составом и не зависит от того, к какому виду она приводится результатом эквивалентных преобразований. Здесь дело только в том, какой из двух векторов (комплексных изображений) принимается за отправной (исходный) и свойств математических действий над функциями – оригиналами и их изображениями. Если в цепи преобладает индуктивность, векторная диаграмма имеет вид рис. 2.23.
Рис. 2.23
Поскольку множитель В этой связи в большинстве случаев комплексную полную проводимость представляют в виде:
При bL > bC, как и в случае Z, цепь носит индуктивный характер, а при bL < bC – емкостной. Легко видеть, что при переводе сопротивления Z в проводимость одной и той же цепи знаки расчетом учитываются автоматически. При построении векторной диаграммы цепи (см. рис. 2.21) с параллельным соединением ветвей за опорный принимают вектор напряжения, одинаковый на всех ветвях, а сама диаграмма представляет собой диаграмму токов, связанных между собою первым законом Кирхгофа, т.е. Понятно, что
Рис. 2.24
Проекция тока Совокупность величин активной
Рис. 2.25
Из этого треугольника легко получить целый ряд зависимостей, которые могут быть полезными при расчетах. Например, Понятно, что треугольник токов при изменении характера цепи при bL < bC остается принципиально одним и тем же. Если все стороны треугольника токов разделить на напряжение U, получим треугольник проводимостей (см. рис. 2.26), поскольку
Рис. 2.26
При этом Понятно, что цепь с параллельным соединением g, bL, bC может быть рассчитана как символическим методом, так и без перевода цепи в комплексную форму. При всех расчетах исходят из того, что при синусоидальном питающем напряжении В области оригиналов:
В области комплексных изображений:
Далее полученные комплексные амплитуды должны быть переведены в оригиналы – синусоиды соответствующих ветвей i(t), iR(t), iL(t), iC(t). При расчете электрических цепей часто приходится прибегать к переводу цепи с последовательным соединением R, xL, xC в эквивалентную цепь с параллельным соединением g, bL и bC и к обратному преобразованию. При выполнении таких преобразований следует четко понимать, что использованные ранее соотношения Легко видеть, что в общем случае:
освобождая дробь от иррациональности в знаменателе,
что было получено при расчете цепи с параллельным соединением g, bL и bC . Таким образом, следует иметь в виду, что при эквивалентных преобразованиях цепей с последовательным соединением е, L, C в параллельное в общих случаях следует использовать соотношения В этом случае, если при последовательном включении цепь имеет индуктивный характер (xL > хC), при ее переводе в эквивалентное параллельное соединение (bL > bC), т.е. характер цепи не изменяется, что составляет одно из основных условий эквивалентности.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 778. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 и
и  . Таким образом, итоговое уравнение электрического равновесия этой цепи:
. Таким образом, итоговое уравнение электрического равновесия этой цепи: .
.


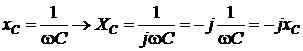 ,
,


 называют полным сопротивлением приемника. В его составе z (малая прописная буква «зет») – модуль (величина) комплексного полного сопротивления Z (большая заглавная буква «зет», иногда обозначаемая Z).
называют полным сопротивлением приемника. В его составе z (малая прописная буква «зет») – модуль (величина) комплексного полного сопротивления Z (большая заглавная буква «зет», иногда обозначаемая Z). и называется просто полным (или кажущимся) сопротивлением приемника, а:
и называется просто полным (или кажущимся) сопротивлением приемника, а: , как будет показано, равен
, как будет показано, равен  , т.е. разности фаз (сдвиг по фазе) между напряжением и током приемника. Он может быть положительным (x > 0) при xL > xC (в цепи преобладает индуктивность, приемник имеет индуктивный характер) и отрицательным (x < 0) при xL < xC (в цепи преобладает емкость, приемник носит емкостной характер).
, т.е. разности фаз (сдвиг по фазе) между напряжением и током приемника. Он может быть положительным (x > 0) при xL > xC (в цепи преобладает индуктивность, приемник имеет индуктивный характер) и отрицательным (x < 0) при xL < xC (в цепи преобладает емкость, приемник носит емкостной характер). и
и  считать законом Ома в комплексной форме.
считать законом Ома в комплексной форме. ®
®  ,
, ®
®  ,
, .
. [Ом], а
[Ом], а  . При этом:
. При этом: и
и  , а
, а  .
. , а
, а  , для идеальной индуктивности Z = jxL и
, для идеальной индуктивности Z = jxL и  , а для емкости z = xС и
, а для емкости z = xС и  .
. на зажимах приемника искомый ток будет синусоидальным, т.е.
на зажимах приемника искомый ток будет синусоидальным, т.е.  .
. .
. .
. .
. :
: .
. :
: ,
, :
: .
.
 путем параллельного переноса векторов.
путем параллельного переноса векторов. . Это означает, что j > 0 (отсчет углов производится против часовой стрелки), что в свою очередь говорит о преобладании в цепи индуктивности (хL > хС), когда общий ток отстает по фазе от напряжения на угол
. Это означает, что j > 0 (отсчет углов производится против часовой стрелки), что в свою очередь говорит о преобладании в цепи индуктивности (хL > хС), когда общий ток отстает по фазе от напряжения на угол  .
. в цепи будет преобладать емкость (цепь носит емкостной характер) и ток будет опережать напряжение на угол
в цепи будет преобладать емкость (цепь носит емкостной характер) и ток будет опережать напряжение на угол  .
. , х = 0 и j = 0, т.е. несмотря на то, что в цепи есть и индуктивность, и емкость по фазе ток и напряжение будут совпадать. Это значит, что цепь, в целом, будет вести себя как только активное сопротивление, когда Z = R + jx = R. Такой режим работы цепи называется резонансным и будет рассмотрен отдельно.
, х = 0 и j = 0, т.е. несмотря на то, что в цепи есть и индуктивность, и емкость по фазе ток и напряжение будут совпадать. Это значит, что цепь, в целом, будет вести себя как только активное сопротивление, когда Z = R + jx = R. Такой режим работы цепи называется резонансным и будет рассмотрен отдельно. , называется активной составляющей напряжения, а на ось, перпендикулярную току, т.е.
, называется активной составляющей напряжения, а на ось, перпендикулярную току, т.е.  , называют реактивной составляющей напряжения. Понятно, что
, называют реактивной составляющей напряжения. Понятно, что  , а
, а  .
. называется треугольником напряжений (рис. 2.19).
называется треугольником напряжений (рис. 2.19).
 .
. , получим треугольник, называемый треугольником сопротивлений z, R и x = xL – xC (рис. 2.20).
, получим треугольник, называемый треугольником сопротивлений z, R и x = xL – xC (рис. 2.20).
 , а также R = z×cosj и x = z×sinj. Конечно,
, а также R = z×cosj и x = z×sinj. Конечно,  и
и  .
.
 ,
,  ,
,  ,
, .
.

 .
.



 и
и  (реактивные проводимости ветвей). При этом
(реактивные проводимости ветвей). При этом  .
. и
и 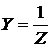 .
. (j = yu – yi > 0, yu > yi), в цепи преобладает индуктивность, то перевод сопротивления этой цепи в проводимость приводит к изменению знака аргумента j на противоположный:
(j = yu – yi > 0, yu > yi), в цепи преобладает индуктивность, то перевод сопротивления этой цепи в проводимость приводит к изменению знака аргумента j на противоположный: .
.
 поворачивает исходный вектор на угол j в положительном направлении (против часовой стрелки) при j > 0, и в отрицательном при j < 0, в случае
поворачивает исходный вектор на угол j в положительном направлении (против часовой стрелки) при j > 0, и в отрицательном при j < 0, в случае 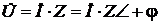 опорным является вектор
опорным является вектор  , а вектор
, а вектор  «поворачивается» от вектора
«поворачивается» от вектора  опорным является
опорным является  .
.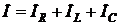 (рис. 2.24).
(рис. 2.24). совпадает по фазе с напряжением,
совпадает по фазе с напряжением,  отстает от напряжения на угол 90°, а
отстает от напряжения на угол 90°, а  – опережает это напряжение на 90°. Диаграмма (см. рис. 2.24) построена исходя из того, что bL > bC, bL > 0, т.е. цепь имеет индуктивный характер, и отстает от напряжения на угол j.
– опережает это напряжение на 90°. Диаграмма (см. рис. 2.24) построена исходя из того, что bL > bC, bL > 0, т.е. цепь имеет индуктивный характер, и отстает от напряжения на угол j.
 , а на ось, перпендикулярную напряжению – реактивной составляющей
, а на ось, перпендикулярную напряжению – реактивной составляющей  .
. , реактивной
, реактивной  составляющей и общего тока
составляющей и общего тока  на плоскости называют треугольником токов (см. рис. 2.25).
на плоскости называют треугольником токов (см. рис. 2.25).
 ,
,  и т.д.
и т.д. ,
,  и
и  .
.
 – модуль (величина) полной комплексной проводимости, g – ее активная, а b – реактивная составляющие. При этом угол
– модуль (величина) полной комплексной проводимости, g – ее активная, а b – реактивная составляющие. При этом угол 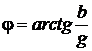 . Все эти зависимости полностью совпадают с полученными ранее. Ясно, что треугольники тока и проводимости подобны.
. Все эти зависимости полностью совпадают с полученными ранее. Ясно, что треугольники тока и проводимости подобны. токи в каждой k-той ветви – тоже синусоидальны, т.е.
токи в каждой k-той ветви – тоже синусоидальны, т.е.  .
. , при
, при  ,
,  ,
, 
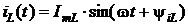 , при
, при  ,
, 
 , при
, при  ,
, 
 , при
, при  ,
,  ,
,  .
.

 ,
, 
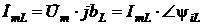


 и
и  ,
,  и
и  ,
, 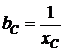 и
и  использованы быть не могут, т.к. сопротивления R, xL, xC в последовательном и эквивалентном параллельном соединении – разные сопротивления.
использованы быть не могут, т.к. сопротивления R, xL, xC в последовательном и эквивалентном параллельном соединении – разные сопротивления. ,
,
 ,
,  и
и  , где
, где  ,
,  и
и  , где
, где  , а
, а  .
.