
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Изображение синусоидальных функций комплексными числами
Легко показать, что любая синусоидальная функция времени, a(t) = Am × sin(wt + y) полностью, определяемая амплитудой Am и фазой (wt + y), однозначно определяется функцией
Это значит, что если нам известна функция a(t) = Am × sin(wt + y), то этой функции однозначно может быть сопоставлена функция Конечно, речь здесь идет не о равенстве, а о взаимно однозначном соответствии, как между конкретным человеком и его паспортом. Именно поэтому можно вести речь о функции – оригинале a(t) = Am × sin(wt + y) и однозначно соответствующем этому оригиналу изображении Понятно, что:
Здесь
Рис. 2.9
При этом комплексное действующее значение будет представлено вектором:
Итак, комплексная амплитуда и комплексное действующее значение представляют не всю синусоиду. Они не учитывают частоту. Вся синусоида на комплексной плоскости представляется комплексной амплитудой, вектор которой вращается против часовой стрелки со скоростью w = const вокруг начала координат от своего первоначального положения
Здесь w – угловая скорость вращения вектора (отсюда w – угловая частота синусоиды).  Как уже было отмечено, при расчетах электрических цепей мы всегда имеем дело с одной единственной, как правило, известной частотой ЭДС, токов и напряжений. В таких случаях вращением векторов с постоянной скоростью можно не считаться, ибо взаимное расположение различных векторов не меняется, а сама частота известна. Таким образом, любая синусоида известной частоты однозначно может быть представлена комплексной амплитудой
Если комплексная амплитуда найдена в виде алгебраической формы
где Примеры. 1.
2. Таким образом, синусоида 3. В показательной форме Комплексное число расположено во втором квадрате плоскости. Следовательно, соответствующая этой комплексной амплитуде синусоида Следует иметь в виду, что постоянные ЭДС, напряжения и токи вполне возможно рассматривать как частные случаи синусоидальных величин. Дело в том, что синусоида
Это означает, что постоянная величина Am
где Am – величина постоянной ЭДС, напряжения или тока (E, V, I). В некоторых случаях при расчете электрических цепей представление постоянных ЭДС, напряжений и токов в виде синусоид оказывается целесообразным. Одновременно это говорит о том, что методы расчета электрических цепей постоянного тока полностью совпадают с методами расчета цепей синусоидального тока в символической форме.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 451. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
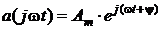 на комплексной плоскости. Это соответствие является взаимно однозначным, поскольку:
на комплексной плоскости. Это соответствие является взаимно однозначным, поскольку:
 .
. называется комплексной амплитудой синусоиды. Соответственно
называется комплексной амплитудой синусоиды. Соответственно  называется комплексным действующим значением. В связи с этим на комплексной плоскости комплексная амплитуда
называется комплексным действующим значением. В связи с этим на комплексной плоскости комплексная амплитуда  представляет собой вектор с длиной (модулем), в соответствующем масштабе равным Am, и поворотом относительно положительной полуоси вещественных в положительном (при +y) направлении (против часовой стрелки) на угол y (рис. 2.9).
представляет собой вектор с длиной (модулем), в соответствующем масштабе равным Am, и поворотом относительно положительной полуоси вещественных в положительном (при +y) направлении (против часовой стрелки) на угол y (рис. 2.9).
 .
.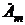 , а именно (рис. ):
, а именно (рис. ): .
. или комплексным действующим значением
или комплексным действующим значением 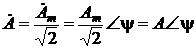 . С другой стороны, при известной частоте по найденной комплексной амплитуде
. С другой стороны, при известной частоте по найденной комплексной амплитуде 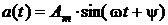 .
.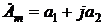 , для нахождения соответствующей синусоиды необходимо вначале перевести
, для нахождения соответствующей синусоиды необходимо вначале перевести  ,
, , а
, а  . Отсюда – синусоида
. Отсюда – синусоида  .
.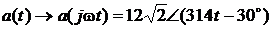 .
. ,
,  .
. – комплексное действующее значение синусоиды. При известной частоте w в цепи получаем
– комплексное действующее значение синусоиды. При известной частоте w в цепи получаем  и
и  .
. .
. .
. .
. .
. .
. на комплексной плоскости представляется, если в этом есть необходимость, комплексным числом:
на комплексной плоскости представляется, если в этом есть необходимость, комплексным числом: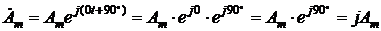 ,
,