
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Соответствие математических операций над синусоидами математическим операциям над их комплексными изображениями
Доказательства таких соответствий достаточно просты и приводятся во всех учебниках по теоретической электротехнике. Как правило, переход от математических операций над синусоидами к математическим действиям над изображающими их комплексными числами существенно упрощает расчеты. I. Сложение и вычитание синусоид. К сожалению, в тригонометрии отсутствуют удобные для инженерных расчетов формулы для сложения и вычитания синусоид. Известно только одно: результатом сложения и вычитания синусоид одной и той же частоты является синусоида той же частоты со своей амплитудой и начальной фазой, которые и нужно определить. Перевод синусоид в область комплексных изображений позволяет легко складывать (или вычитать) любое количество синусоид, ибо сложению и вычитанию синусоид соответствует сложение или вычитание изображающих эти синусоиды комплексных чисел. Так что, если:
Поскольку сложение и вычитание комплексных чисел удобнее проводить в алгебраической форме, показательные формы Пример.
Требуется сложить эти две синусоиды, т.е.:
Таким образом, нужно определить Am и y. Обычными тригонометрическими правилами (тем более в случае более двух синусоид) это сделать или чрезвычайно трудно, или даже невозможно. Но
Следовательно, Это и есть итоговая синусоида. Искомые Am = 11,8, а y = 41°.
II. Умножение и деление синусоиды на вещественную постоянную. Умножению синусоиды на вещественную постоянную «k» (если k = 1/P – дробное, то делению) в области комплексных изображений соответствует умножение (деление) на эту постоянную комплексного изображения синусоиды  Если В этом случае в комплексной амплитуде (комплексном действующем значении) изменяется только модуль (величина), а аргумент остается прежним. На комплексной плоскости
III. Дифференцирование синусоиды. Если В области комплексных изображений, когда
Пример.
К дифференцированию синусоиды приходится прибегать при использовании закона электромагнитной индукции (Фарадей).
IV. Интегрирование синусоиды Если
где Это значит, что проинтегрированная синусоида отстает от исходной на угол К интегрированию синусоиды приходится прибегать при анализе емкости в цепи. Отсутствие здесь постоянной интегрирования, представляющей собой среднее значение интегрируемой функции, объясняется тем, что среднее за период значение синусоиды равно нулю, т.е. постоянная составляющая в нашем случае отсутствует. Легко видеть, что перечисленные фактически уникальные для синусоид и их комплексных изображений свойства позволяют дифференциальные уравнения электрического равновесия электрических цепей заменить простыми алгебраическими уравнениями, что не просто облегчает расчет, но в некоторых случаях только и позволяет его выполнить. Например, система дифференциальных уравнений, приведенная в п.1.8 для электрической цепи (рис. 14) легко приводится к системе простых алгебраических уравнений: 1. 2. I. II. III.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 514. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
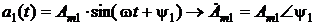 , а
, а
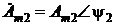 , то
, то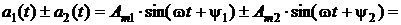
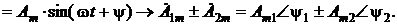
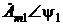 и
и 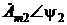 необходимо привести в алгебраическую форму.
необходимо привести в алгебраическую форму.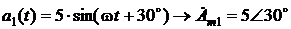
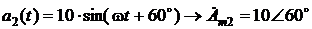 .
.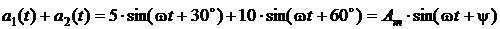 .
.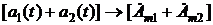 . Для этого
. Для этого 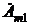 и
и 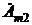 переводим в начале в алгебраическую, а затем в показательную формы:
переводим в начале в алгебраическую, а затем в показательную формы: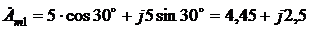
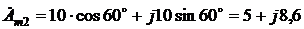
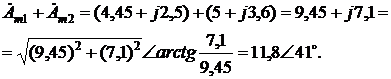

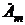 или
или 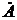 .
.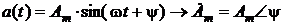 , то
, то 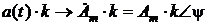 . При этом
. При этом 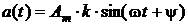 .
.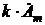 представляют векторы, разной длины при совпадении по направлению. Умножение и деление синусоиды на вещественную постоянную производится в законе Ома для участка цепи с R.
представляют векторы, разной длины при совпадении по направлению. Умножение и деление синусоиды на вещественную постоянную производится в законе Ома для участка цепи с R.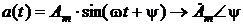 , то
, то 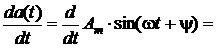
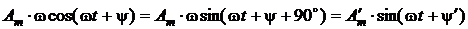 . Таким образом, результатом дифференцирования синусоиды оказывается синусоидальная функция той же самой частоты, что является принципиально важным для электрических цепей синусоидального тока. Но амплитуда
. Таким образом, результатом дифференцирования синусоиды оказывается синусоидальная функция той же самой частоты, что является принципиально важным для электрических цепей синусоидального тока. Но амплитуда 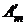 новой синусоиды больше исходной в w раз, т.е.
новой синусоиды больше исходной в w раз, т.е. 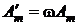 , а начальная фаза этой синусоиды увеличивается на 90°, т.е.
, а начальная фаза этой синусоиды увеличивается на 90°, т.е. 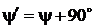 . Это значит, что продифференцированная синусоида опережает исходную на 90° = p/2.
. Это значит, что продифференцированная синусоида опережает исходную на 90° = p/2.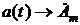 получаем, что комплексная амплитуда новой синусоиды
получаем, что комплексная амплитуда новой синусоиды 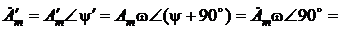
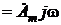 . Это значит, что относительно сложное математическое действие, связанное с дифференцированием в области комплексных изображений заменяется на обычное алгебраическое, а именно – на умножение комплексного изображения исходной синусоиды на множитель jw, что существенно упрощает расчеты.
. Это значит, что относительно сложное математическое действие, связанное с дифференцированием в области комплексных изображений заменяется на обычное алгебраическое, а именно – на умножение комплексного изображения исходной синусоиды на множитель jw, что существенно упрощает расчеты.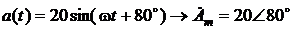 .
.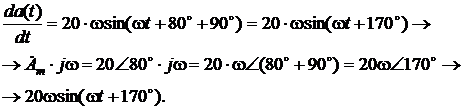
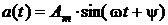 , то
, то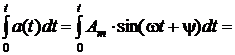
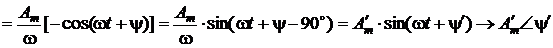 ,
,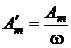 уменьшается в w раз, а
уменьшается в w раз, а 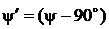 уменьшается на 90° =
уменьшается на 90° = 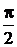 .
.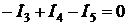 ;
;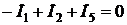 ;
;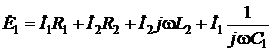 ;
;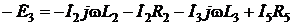 ;
;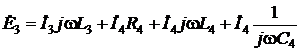 .
.