
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Математические действия над комплексными числами
Математические операции над комплексными числами полностью подчиняются правилам обычной школьной алгебры. I. Сложение и вычитание комплексных чисел производятся по правилам приведения подобных в алгебраической форме записи чисел: (a1 + ja2) ± (b1 + jb2) = a1 + ja2 ± b1 + jb2 = (a1 ± b1) + j(a2 ± b2) = c1 + jc2, где с1 = (a1 ± b1) – вещественная часть суммы двух чисел, а c2 = (a2 ± b2) – мнимая. При этом следует иметь в виду, что у a1, b1, a2, b2 могут иметь собственные знаки (плюс или минус), которые, безусловно, должны учитываться. Процедуры сложения
Рис. 2.8 Таким образом, сложению и вычитанию комплексных чисел соответствует сложение и вычитание векторов этих комплексных чисел. Этот очевидный факт оказывается чрезвычайно полезным при построении векторных диаграмм участков электрических цепей и цепей в целом. Примеры. 1. (3 + j5) + (2 – j8) = (3 + 2) + j(5 – 8) = 5 – j3. 2. (6 – j4) – (3 – j5) = (6 – j4 – 3 + j5) = (6 – 3) + j(–4 + 5) = 3 + j.
II. Умножение и деление комплексных чисел удобнее всего производить в показательной форме по правилам умножения и деления степенных чисел:
где С = А × В, а g = a + b. Соответственно:
где Понятно, что при всех этих операциях должны учитываться собственные знаки аргументов a и b. Пример. Если
III. Умножение комплексного числа на постоянную k. В соответствии с правилом умножения (деления):
где С = А × k, при этом «k» может быть дробью, т.е. k = 1/Т. В комплексном числе в этом случае изменяется только модуль без изменения аргумента. Легко видеть, что умножению комплексного числа на постоянную приводит к умножению вектора, соответствующего комплексному числу, на эту постоянную, что приводит к увеличению (при делении – к уменьшению) модуля (длины) вектора без изменения его положения относительно осей координат.  Пример. Если
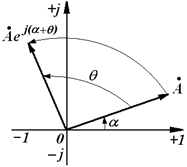
IV. Умножение комплексного числа на множитель Если Результат показан на рис. 2.8.
Рис. 2.8
Это значит, что умножение комплексного числа В частности, это значит, что если вещественную положительную единицу (+1) умножить на Понятно, что j2 = –1 и Все эти соотношения оказываются чрезвычайно полезными при вычислениях с комплексными числами. Исключительно важным для символического метода является умножение комплексного числа на множитель Вектор комплексного числа Два комплексных числа с одинаковыми модулями, но противоположными по знаку аргументами называются сопряженными. Например, если
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 426. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
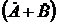 и вычитания
и вычитания 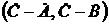 векторов, соответствующих комплексным числам
векторов, соответствующих комплексным числам 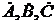 наглядно иллюстрируются рисунком 2.7.
наглядно иллюстрируются рисунком 2.7.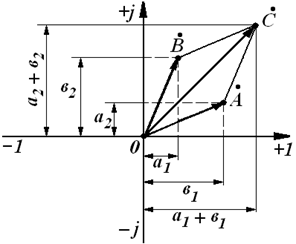
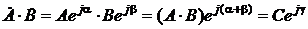 ,
, ,
,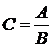 , а g = a – b.
, а g = a – b.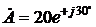 , а
, а 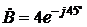 , то
, то 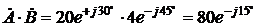 и
и 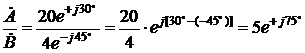 .
.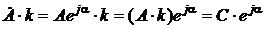 ,
,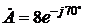 , а k = 6, то
, а k = 6, то 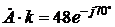 .
. приводит к следующему.
приводит к следующему.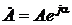 , то
, то 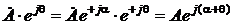 .
.
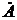 на
на 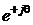 приводит к повороту вектора, соответствующего числу
приводит к повороту вектора, соответствующего числу 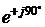 , получим положительную мнимую единицу, т.е.
, получим положительную мнимую единицу, т.е. 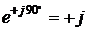 . Значит,
. Значит, 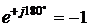 ,
, 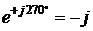 ,
, 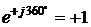 ,
, 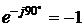 .
.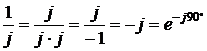 .
.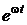 при w = const и изменении времени t от 0 до ¥.
при w = const и изменении времени t от 0 до ¥.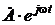 во времени совершает круговое вращение относительно начала координат «0» против часовой стрелки с постоянной скоростью (угловой частотой) w = const.
во времени совершает круговое вращение относительно начала координат «0» против часовой стрелки с постоянной скоростью (угловой частотой) w = const.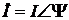 , то сопряженное ему число
, то сопряженное ему число 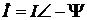 .
.