
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Решение задачи методом Понтрягина⇐ ПредыдущаяСтр 23 из 23 Введём для этого допущения: -неучитывая ограничения g(x(t))≤0
Для
Пусть функционал
при t=T и
 Коэффициенты Возможно три варианта решения вариационной задачи: 2. На всём отрезке t: 0≤t≤T 3. На отрезке t: 0≤t≤ На отрезке огранич
Время
Условия конкурентоспособности боевых ЛА Условия формулируются в форме сопоставления коэффициентов значимости E(t) различных типов ЛА на отрезке 0≤t≤T, где T – глубина прогнозирования. Два варианта ЛА j-й и i-й конкурентоспособны, если на отрезке 0≤t≤ Они применяются для: 1. 2. Показатели Условия конкурентоспособности определяются для случаев: А. ЛА i-го варианта предпочтительнее ЛА j-го варианта в будущем моменте t=T, если Так как Назовем ЛА i-го варианта, для которого выполняется (9), - базовым.
Вариационная задача прогнозирования развития системы ТСЛА Формулировка задачи Эта модель в отличие от рассмотренной модели прогнозирования развития боевых систем ЛА прогнозирует создание системы, способной дать наибольший результат не в конечном моменте времени , то есть время начала предполагаемого применения боевой СЛА, а за весь будущий отрезок t прогнозирования 0≤t≤T.
Требуется определить оптимальную управляющую вариационную функцию
Решение задачи методом Понтрягина В соответствии с методом Понтрягина, оптимальное управление доставляет максимальное значение уравнения Гамильтона Н. Функция Гамильтона имеет вид: Для 0≤t≤T: Так как для всех ЛА i-го варианта числитель функции q одинаков при сравнении
При условии t=T, Для случая, когда оптимальная система должна комплектоваться летательными аппаратами двух вариантов: j-го и i-го, оптимальное решение записывается так:
Условия конкурентоспособности транспортных ЛА А. Моменты времени t, примыкающие к T(т.еt≈T). ТЛА i-го варианта предпочтительнее ТЛА j-го варианта, если
ЛА i-го варианта считаются базовыми Б. ТЛА j-го варианта конкурируют с ТЛА i-го варианта, если Шиленок
Т.е. 3. Вариационная обратная задача с функционалом, представляет собой затраты на создание и эксплуатацию системы с заданным на промежутке 0 ≤t≤T значениями КФЭ, то есть
4. Игровая прямая задача (дифф.Игра), в которой отыскиваются оптимальные траектории развития двух противоборствующих сторон X и Y при заданных ассигнованиях. При строгом соперничестве: При нестрогом соперничестве:
Где Модели прогнозирования развития ТСЛА 3. Вариационная прямая задача с функционалом представляет собой эффективность функционирования ТСЛА за отрезок будущего времени 0 ≤t≤T 4. Вариационная обратная задача с функционалом, представляет затраты на создание и эксплуатацию системы с заданным функциональным эффектом за Т, то есть: 5.
Векторное число ЛА x(t) подчиняется: а) векторным ограничениям: x(t)≥0 g(x(t))≤0 где g – векторное ограничение на число ЛА б) Дифференциальными уравнениями (1) Где i=1,2,…., n – число вариантов ЛА, из которых может быть сформирована СЛА
(2)Управляющие функции То есть, при Оптимальное уравнение
Вариационная прямая задача прогнозирования развития боесистем ЛА Формулировка задачи: Пусть в момент t=0 когда надо выработать прогноз развития БСЛА на отрезке будущего времени известны: 6. Назначение; боезадачи БСЛА, критерий боевой функции, эффективность 7. Облик и обобщённые характеристики 8. Число серийных ЛА i-го варианта при t=0, 9. Интегральное уравнение на развитие СЛА 10. Характеристики СЛА стороны Y, противодействующей стороне X. Определить оптимальную управляющую вариативную функцию
при условиях 1,2, а так же
Решение задачи методом Понтрягина Введём для этого допущения: -не учитывая ограничения g(x(t))≤0 -полагаем независящими от времени показатели боевой эффективности i-го ЛА стороны x -функционал С методом Понтрягина, оптимальное управление доставляет максимальное значение функций Гамильтона H, то есть:
Гамильтониан в этом случае Для
Пусть функционал
(6)
Его можно не учитывать и представить (7)
Проанализируем решение (4) вариационной задачи (3): Оптимальное уравнение То есть ЛА j-го варианта превосходит ЛА i-го варианта и все ресурсы, отпускаемые на производство, расходуются на ЛА j-го типа Это так или иначе принимается концентрацией усилий: если ресурсы ограничены, то их тратят на самое важное Если на Коэффициенты Рассмотрим вопрос сравнения ЛА разных вариантов подробно Пусть СЛА состоит из двух типов i-го и j-го. Без потери общности можно считать, что ЛА j-го варианта находится на вооружении в момент времени t=0, и их число Возможно три варианта решения вариационной задачи: 1. На всем отрезке времени прогнозируется 0≤t≤T 2. На всём отрезке t: 0≤t≤T 3. На отрезке t: 0≤t≤
Время
Условия конкурентоспособности боевых ЛА Условия формулируются в форме сопоставления коэффициентов значимости E(t) различных типов ЛА на отрезке 0≤t≤T, где T – глубина прогнозирования. Два варианта ЛА j-й и i-й конкурентоспособны, если на отрезке 0≤t≤
В этом случае СЛА формируется из трёх вариантов (I,j,k) Условия монопольности ЛА i-го варианта на всем отрезке 0≤t≤T определяется так: Тот или иной вариант оптимальной СЛА определяется путем решения задачи (3) Условия конкурентоспособности ЛА еще могут быть представлены в косвенной форме через обобщенные показатели Косвенные условия конкурентоспособности ЛА Они применяются для: 3. 4. Показатели Условия конкурентоспособности определяются для случаев: А. ЛА i-го варианта предпочтительнее ЛА j-го варианта в будущем моменте t=T, если Так как
Назовем ЛА i-го варианта, для которого выполняется (9), - базовым. Б. ЛА j-го варианта конкурирует с ЛА i-го варианта, если время перехода на производство ЛА i-го варианта не равно 0, то есть Это означает, что на Для того, чтобы ЛА j-го варианта был конкурентоспособен по отношению к ЛА i-го варианта необходимо выполнение:
Для установления конкурентоспособности ЛА необходимо: 1. Выявить базовый ЛА i-го варианта в t=Tc соотношения (8) или (9) 2. Проверить конкурентоспособность ЛА j-го варианта по отношению к ЛА i-го варианта с помощью (10)
Вариационная задача прогнозирования развития системы ТСЛА Формулировка задачи Эта модель в отличие от рассмотренной модели прогнозирования развития боевых систем ЛА прогнозирует создание системы, способной дать наибольший результат не в конечном моменте времени, то есть время начала предполагаемого применения боевой СЛА, а за весь будущий отрезок t прогнозирования 0≤t≤T. Формулировка вариационной задачи в общем виде была приведена ранее. Конкретизируем её. Для этого конкретизируем функционал
В качестве функции
Требуется определить оптимальную управляющую вариационную функцию
Решение задачи методом Понтрягина В соответствии с методом Понтрягина, оптимальное управление доставляет максимальное значение уравнения Гамильтона Н.
Функция Гамильтона имеет вид:i Для 0≤t≤T: Так как для всех ЛА i-го варианта числитель функции q одинаков при сравнении
При условии t=T, Для случая, когда оптимальная система должна комплектоваться летательными аппаратами двух вариантов: j-го и i-го, оптимальное решение записывается так:
Условия конкурентоспособности транспортных ЛА А. Моменты времени t, примыкающие к T(т.еt≈T). ТЛА i-го варианта предпочтительнее ТЛА j-го варианта, если
ЛА i-го варианта считаются базовыми Б. ТЛА j-го варианта конкурируют с ТЛА i-го варианта, если
Условие монопольности ТЛА i-го варианта имеет вид:
То есть при данных условиях целесообразно производить только ЛА i-го варианта. Условия монопольности ТЛА j-го варианта, характеризующая целесообразность производства только ТЛА этого варианта, имеет вид:
|
||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 416. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 и стороны y
и стороны y 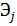
 считаем практически не зависящим от
считаем практически не зависящим от 
 при 0≤
при 0≤  ,
, 

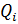 – правые части уравнений развития СЛА
– правые части уравнений развития СЛА 



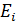 – Коэффициент значимости ЛА i-го типа в СЛА
– Коэффициент значимости ЛА i-го типа в СЛА - Критерий боевой эффективности одного ЛА i-го типа, функционирующего в системе
- Критерий боевой эффективности одного ЛА i-го типа, функционирующего в системе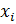 , то есть:
, то есть:  и представляет собой, например, математическое ожидание числа уничтоженных истребителями ВЦ за время операции.
и представляет собой, например, математическое ожидание числа уничтоженных истребителями ВЦ за время операции. - сопряженная функция. Она сопрягается интегральным сопряжением уравнений.
- сопряженная функция. Она сопрягается интегральным сопряжением уравнений. (6)
(6) , так как для всех ЛА i-го типа числитель функции
, так как для всех ЛА i-го типа числитель функции  - одинаков при сравнении
- одинаков при сравнении 

 (7)
(7) - удельная боевая эффективность ЛА i-го типа, то есть величина критерия боевой эффективности ЛА i-го типа, приходящаяся на единицу стоимости его создания
- удельная боевая эффективность ЛА i-го типа, то есть величина критерия боевой эффективности ЛА i-го типа, приходящаяся на единицу стоимости его создания 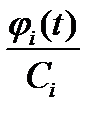 - функция, учитывающая влияние будущего времени на значимость ЛА i-го варианта
- функция, учитывающая влияние будущего времени на значимость ЛА i-го варианта определяется в результате интегрирования уравнений (6)
определяется в результате интегрирования уравнений (6)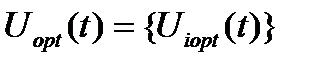 - кусочно-постоянная функция, принимающая на интервале 0≤t≤T значения или 0 или 1. Значимость ЛА i-го варианта определяется функцией
- кусочно-постоянная функция, принимающая на интервале 0≤t≤T значения или 0 или 1. Значимость ЛА i-го варианта определяется функцией  , если на некотором отрезке
, если на некотором отрезке  , то это означает, что на этом отрезке
, то это означает, что на этом отрезке 
 и ЛА i-го типа превосходит ЛА j-го типа
и ЛА i-го типа превосходит ЛА j-го типа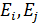 можно назвать динамическими критериями сравнения ЛА i-го и j-го варианта.
можно назвать динамическими критериями сравнения ЛА i-го и j-го варианта.
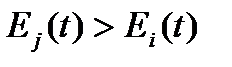 . Это значит
. Это значит  из этого следует, что ЛА j-го варианта превосходит ЛА i-го варианта и СЛА комплектуется только из ЛА j-го варианта. Их число определяется интегральным уравнением (1)
из этого следует, что ЛА j-го варианта превосходит ЛА i-го варианта и СЛА комплектуется только из ЛА j-го варианта. Их число определяется интегральным уравнением (1) и система ЛА состоит только из ЛА i-го варианта. Численность ЛА определяется интегральным уравнением (1)
и система ЛА состоит только из ЛА i-го варианта. Численность ЛА определяется интегральным уравнением (1) ,
, 

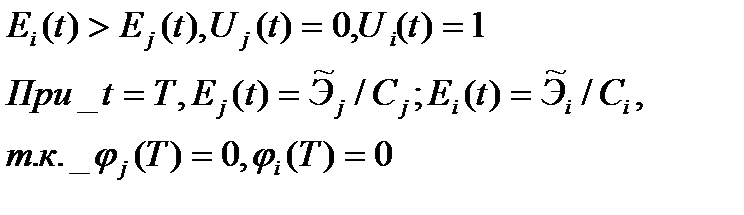
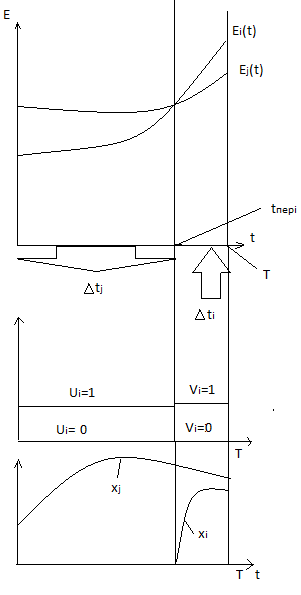
 , где E определяются выражением (7)
, где E определяются выражением (7)
 - время перехода с производства ЛА j-го варианта на производство ЛА i-го варианта. В этом случае СЛА формируются из ЛА двух типов. Три варианта ЛА конкурентоспособны, если на отрезке 0≤t≤
- время перехода с производства ЛА j-го варианта на производство ЛА i-го варианта. В этом случае СЛА формируются из ЛА двух типов. Три варианта ЛА конкурентоспособны, если на отрезке 0≤t≤  , на отрезке
, на отрезке 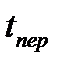 k≤t≤
k≤t≤  , на отрезке
, на отрезке  ≤t≤T,
≤t≤T, 
 - времена переходов СЛА j-го варианта на ЛА к-го варианта и с производства к-го варианта на ЛА i-го варианта.
- времена переходов СЛА j-го варианта на ЛА к-го варианта и с производства к-го варианта на ЛА i-го варианта.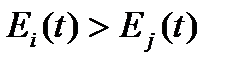

 - const
- const
 , условия:
, условия:

 производился ЛА j-го варианта.
производился ЛА j-го варианта.

 , характеризующую суммарную результативность функционирования ТСЛА в ед. t выделим:
, характеризующую суммарную результативность функционирования ТСЛА в ед. t выделим:
 - Коэффициент важности i-го ЛА
- Коэффициент важности i-го ЛА - Интенсивность функционирования ЛА i-го варианта
- Интенсивность функционирования ЛА i-го варианта 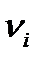 - летная доля суток
- летная доля суток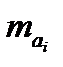 - масса, перевозимой ЛА i-го варианта, нагрузки
- масса, перевозимой ЛА i-го варианта, нагрузки - дальность полета
- дальность полета - время рейса
- время рейса
 - средняя крейсерская скорость
- средняя крейсерская скорость - пассивное время
- пассивное время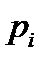 - вероятность выполнения полетного задания Летательным Аппаратом i-го варианта
- вероятность выполнения полетного задания Летательным Аппаратом i-го варианта и оптимальный прогноз
и оптимальный прогноз  , обеспечивающие максимальное значение функционала
, обеспечивающие максимальное значение функционала при условиях (1),(2),
при условиях (1),(2), 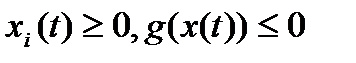


 , то его можно не учитывать и тогда можно представить:
, то его можно не учитывать и тогда можно представить: 
 - коэффициент значимости ЛА i-го варианта в ТСЛА
- коэффициент значимости ЛА i-го варианта в ТСЛА - Сопряженная функция
- Сопряженная функция  , определяется интегральным сопряжением уравнений:
, определяется интегральным сопряжением уравнений:
 =0
=0

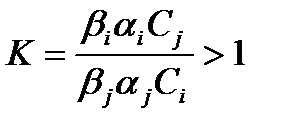




 (X
(X  )) =
)) = 
 (X(t))
(X(t))

 – Стоимость создания БСЛА
– Стоимость создания БСЛА


 – критерии функциональной эффективности систем Х и Y
– критерии функциональной эффективности систем Х и Y


 , где
, где  - числа вариантов серийных и новых ЛА
- числа вариантов серийных и новых ЛА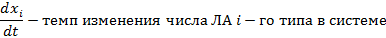

 -максимальный темп поступления ЛА i-го типа в системе.с производством
-максимальный темп поступления ЛА i-го типа в системе.с производством – интенсивность ассигнований на развитие системы ЛА
– интенсивность ассигнований на развитие системы ЛА

 – годовая стоимость эксплуатации ЛА i-го вер-та
– годовая стоимость эксплуатации ЛА i-го вер-та – стоимость продажи ЛА i-го типа за рубеж
– стоимость продажи ЛА i-го типа за рубеж – интенсивность продажи ЛА i-го типа за рубеж
– интенсивность продажи ЛА i-го типа за рубеж – доля дохода от продажи ЛА за рубеж, которая выделяется на развитие СЛА (0≤
– доля дохода от продажи ЛА за рубеж, которая выделяется на развитие СЛА (0≤  )
) – стоимость создания ЛА i-го варианта
– стоимость создания ЛА i-го варианта - суммарная интенсивность выбытия ЛА i-го варианта из системы ЛА
- суммарная интенсивность выбытия ЛА i-го варианта из системы ЛА – темп выбытия ЛА i-го варианта из-за гибели и продажи за рубеж
– темп выбытия ЛА i-го варианта из-за гибели и продажи за рубеж – интенсивность гибели ЛА i-го варианта
– интенсивность гибели ЛА i-го варианта – управление, представляющее собой долю средств, выделяемую в момент t на производство ЛА i-го типа
– управление, представляющее собой долю средств, выделяемую в момент t на производство ЛА i-го типа ≤1,
≤1, 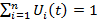
 на производство ЛА i-го типа средств не выделяется, при
на производство ЛА i-го типа средств не выделяется, при 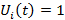 средства выделяются. Если на отрезке 0≤t≤T управляющие функции
средства выделяются. Если на отрезке 0≤t≤T управляющие функции  ,
,  (
( 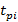 – время завершения разработки ЛА i-го типа)
– время завершения разработки ЛА i-го типа)  позволяет найти траекторию развития СЛА i-го типа.
позволяет найти траекторию развития СЛА i-го типа. даёт оптимальную траекторию(прогноз) развития системы ЛА
даёт оптимальную траекторию(прогноз) развития системы ЛА
 определяются в результате решения вариационных задач
определяются в результате решения вариационных задач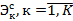 и скалярная композиция
и скалярная композиция 
 существующих и перспективных ЛА i-го типа
существующих и перспективных ЛА i-го типа  из которых на отрезке времени 0≤t≤T прогноз.дбсформиров БСЛА
из которых на отрезке времени 0≤t≤T прогноз.дбсформиров БСЛА


 ,
,  , обеспечивающие максимальное значение функционала в момент t=T
, обеспечивающие максимальное значение функционала в момент t=T
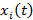 ≥0, g(
≥0, g(  и стороны y
и стороны y 
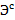 считаем практически не зависящим от
считаем практически не зависящим от 
 при 0≤
при 0≤  ,
, 
 – правые части уравнений развития СЛА
– правые части уравнений развития СЛА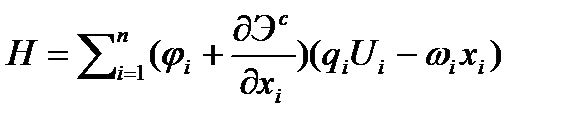
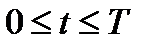

 – Коэффициент значимости ЛА i-го типа в СЛА
– Коэффициент значимости ЛА i-го типа в СЛА - Критерий боевой эффективности одного ЛА i-го типа, функционирующего в системе
- Критерий боевой эффективности одного ЛА i-го типа, функционирующего в системе , то есть:
, то есть:  при t=T и
при t=T и 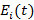 , если на некотором отрезке
, если на некотором отрезке  можно назвать динамическими критериями сравнения ЛА i-го и j-го варианта.
можно назвать динамическими критериями сравнения ЛА i-го и j-го варианта. ,
, 


