
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Определение программы развития парка АК.Пусть
Введем для оперирующей стороны => обозначения i=
В-ра
Где
E*(t), E(t) – потребное и располагаемые значения показателей целевой эффективности парка АК Для противника введем обозначения: Ψ= dΨ= Известно :
Прогноз развития по численности комплексов против Ψ-го типа Пусть Будем характеризовать при заданных
Где

дефенит целевой эффективности при реализации р-ой программы.
z=z (t)- вариант случайных и неопределенных факторов Введем лесина-графическую упорядоченность в равенстве т. е:
Задача заключается в том, чтобы H: такие
А N’(t), M’(t) / N’(t)є N(t), M’(t)є M(t) удовлетворяет => условиям
Т.о. ход решения задачи состоит в =>: 1. Из множества реализуемых вариантов программ N(t) M(t) выделяются варианты N’, M’ обеспечивают минимальное время входа на потребную эффективность E*(t) Если ∃! Решение, то они и являются оптимальными Если решение неоднозначное, то выделяется множества N’(t) M’(t), к которым они принадлежат 2. Далее из множества N’(t) M’(t), выделяются N’’(t) M’’(t), которые обеспечивают минимум дефицита эффективности 3. Из множества N’’(t) M’’(t) выделяется вариант программы Динамические модели прогнозирования Оптимального развития авиационных систем (АС) (парка летательных аппаратов) Виды моделей и их формулировка АС (парк ЛА) (СПА) – совокупность ЛА с средствами не бортового обеспечения полетов, отличающихся параметрами или назначением и функционирующих для достижения единой цели. При выбранных способах и условиях применения ЛА свойства СЛА определяется числом вариантов ЛА n, в-ром числа ЛА i-го варианта x={ Прогноз развития СЛА на будущем отрезке t: Задача заключается в том, чтобы найти: оптимальный прогноз, траекторию развития СЛА Если в результате решения задачи окажется, например, что 1 группа. Системы, применение которых предполагается в некоторый будущий момент t=T, где T-глубина прогнозирования Время Назовем эти СЛА – боевыми (БСЛА) 2 группа. Системы, применение которых предполагается в ∀ момент будущего времени. Такие системы – транспортные (ТСЛА) 3 группа. Системы, представляющие собой комбинацию БиТСЛА. Рассмотрим формулировки некоторых моделей прогнозирования БиТСЛА. Модели прогнозирования развития БСЛА. 1 Вариационная прямая задача с функционалом, представляющим собой функциональную эффективность БСЛА в момент t=T
Результат выполнения K-ой боевой задачи Критерий оптимизации – это или скалярная композиция вида:
Величина Предполагается, что траектория развития СЛА стороны Y, то есть Y(T),-известна. Примерами функционала 2. Вариационная прямая задача с функционалом, представляет собой t, за которое КФЭ СЛА достигается заданного значения То есть Лекция № ??? (дд.мм.гг) (№12Шиленок)
3. Вариационная обратная задача с функционалом, представляет собой затраты на создание и эксплуатацию системы с заданным на промежутке 0 ≤t≤Tзначениями КФЭ, то есть
4. Игровая прямая задача (дифф. Игра), в которой отыскиваются оптимальные траектории развития двух противоборствующих сторон X и Y при заданных ассигнованиях. При строгом соперничестве: При нестрогом соперничестве: Где Модели прогнозирования развития ТСЛА 1. Вариационная прямая задача с функционалом представляет собой эффективность функционирования ТСЛА за отрезок будущего времени 0 ≤t≤T 2. Вариационная обратная задача с функционалом, представляет затраты на создание и эксплуатацию системы с заданным функциональным эффектом заТ, то есть:
Векторное число ЛА x(t) подчиняется:
а) векторным ограничениям:
б) Дифференциальными уравнениями
Управляющие функции
То есть, при
Вариационная прямая задача прогнозирования развития Формулировка задачи: 1. Назначение; боезадачи БСЛА, критерий боевой функции, эффективность 2. Облик и обобщённые характеристики 3. Число серийных ЛА i-го варианта при t=0, 4. Интегральное уравнение на развитие СЛА 5. Характеристики СЛА стороны Y, противодействующей стороне X.
|
||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 309. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 – начальный и конечный моменты времени планируемого периода T. Текущее время
– начальный и конечный моменты времени планируемого периода T. Текущее время
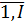 – тип самолета носителя
– тип самолета носителя – тип средств вооружения
– тип средств вооружения ,
,  ,
,  вариант функции от времени обликовых характеристик самолетов носителей и СП, выбираемые на этапе внешнего проектирования. Сюда же включяют уже разработанные и имеющиеся на вооружении
вариант функции от времени обликовых характеристик самолетов носителей и СП, выбираемые на этапе внешнего проектирования. Сюда же включяют уже разработанные и имеющиеся на вооружении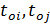 - min возможные времена начала серийного производства самолетов носителей и средств вооружения
- min возможные времена начала серийного производства самолетов носителей и средств вооружения

 связанные с уровнем развития технологий, элементной базы, возможными договорными регламентациями.
связанные с уровнем развития технологий, элементной базы, возможными договорными регламентациями. численность имеющихся к моменту t самолетов носителей i-го типа и с вооружением j-го типа.
численность имеющихся к моменту t самолетов носителей i-го типа и с вооружением j-го типа.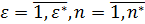 - номера заводов, производящих самолеты носители и СП.
- номера заводов, производящих самолеты носители и СП. носителя i-го типа и 1-го образца СП j-го типа.
носителя i-го типа и 1-го образца СП j-го типа. – располагаемые суммарные трудоресурсы заводов
– располагаемые суммарные трудоресурсы заводов 

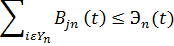


 ограничения, связанные с договорными регламентами
ограничения, связанные с договорными регламентами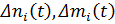 – естественная убыль СП и самолета носителя, где
– естественная убыль СП и самолета носителя, где – множества типов самолетов носителей и СП, которые одновременно производятся на заводах
– множества типов самолетов носителей и СП, которые одновременно производятся на заводах
 - тип АК противника.
- тип АК противника. ,
,  – прогнозируемый вариант технической характеристики АК противника
– прогнозируемый вариант технической характеристики АК противника
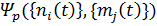 – р-ый вариант программы развития парка p є
– р-ый вариант программы развития парка p є 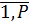
 p-ую программу развития парка вектором из компонент:
p-ую программу развития парка вектором из компонент: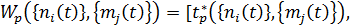 Δp
Δp  ,
, 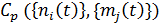 ]
] =min
=min 
 при реализации p-программы
при реализации p-программы
 – стоимость реализации р-ой программы, куда включены затраты на разработку, производство, закупку, эксплуатацию, утилизацию.
– стоимость реализации р-ой программы, куда включены затраты на разработку, производство, закупку, эксплуатацию, утилизацию.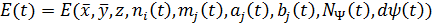
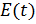 – показатель целевой эффективности группировки.
– показатель целевой эффективности группировки. – стратегии применения оперирующей стороной своих средств
– стратегии применения оперирующей стороной своих средств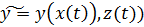 – стратегии применения противником своих СП
– стратегии применения противником своих СП
 и
и 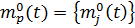 , при этом
, при этом  и ,=>,
и ,=>,  что при заданных
что при заданных  мы имеем:
мы имеем: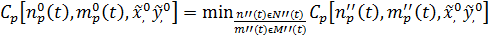 , где N’’(t), M’’(t) находятся из условия:
, где N’’(t), M’’(t) находятся из условия: ,
,
 – оптимальная стратегия оперирующей стороны и противника для заданного варианта z.
– оптимальная стратегия оперирующей стороны и противника для заданного варианта z. , которое обеспечивает минимизацию затрат. (Если решений несколько выбираются ∀)
, которое обеспечивает минимизацию затрат. (Если решений несколько выбираются ∀)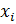 },
}, 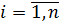 , критериями функциональной эффективности (КФЭ), ∀-гоi-го варианта ЛА, Эi, его отраслевой стоимостью
, критериями функциональной эффективности (КФЭ), ∀-гоi-го варианта ЛА, Эi, его отраслевой стоимостью 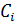 (стоимость разработки и серийные права) и стоимостью эксплуатации в единице t
(стоимость разработки и серийные права) и стоимостью эксплуатации в единице t  . Эти характеристики определяют КФЭ системы
. Эти характеристики определяют КФЭ системы 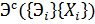 и стоимость создания и эксплуатации системы.
и стоимость создания и эксплуатации системы.  ,
,  Характеризуется векторной функцией x(t)
Характеризуется векторной функцией x(t)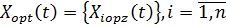
 в какой то момент t=0, то это будет означать, что ЛА n-го варианта системы не нужен, то есть он неперспективен. Все СЛА можно разделить на 3 группы
в какой то момент t=0, то это будет означать, что ЛА n-го варианта системы не нужен, то есть он неперспективен. Все СЛА можно разделить на 3 группы – мирное, время
– мирное, время 
 при заданных ассигнованиях на развитие БСЛА предназначенной для выписывания K боевых задач
при заданных ассигнованиях на развитие БСЛА предназначенной для выписывания K боевых задач
 характеризуется КФЭ
характеризуется КФЭ 
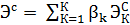 , где
, где  - коэфициент значимости k-ой боевой задачи
- коэфициент значимости k-ой боевой задачи , или
, или  , например,
, например,  с переводом остальных в ограничивающие условия
с переводом остальных в ограничивающие условия в момент Т зависит от вариантов чисел ЛА в СЛА стороны Х, то есть Х(Т), и стороны Y, противодействующей стороне Х, то есть Y(T)
в момент Т зависит от вариантов чисел ЛА в СЛА стороны Х, то есть Х(Т), и стороны Y, противодействующей стороне Х, то есть Y(T) может быть М.О. числа уничтоженных в военное время
может быть М.О. числа уничтоженных в военное время  ВЦ-системой истребителей и НЦ-системной ударных ЛА.
ВЦ-системой истребителей и НЦ-системной ударных ЛА. , то есть Н:
, то есть Н: 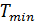 , за которое
, за которое  при
при 
 .
. (X
(X  )) =
)) = 


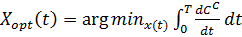
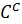 – Стоимость создания БСЛА
– Стоимость создания БСЛА


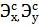 – критерии функциональной эффективности систем Х и Y
– критерии функциональной эффективности систем Х и Y



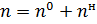 , где
, где  - числа вариантов серийных и новых ЛА
- числа вариантов серийных и новых ЛА 

 -максимальный темп поступления ЛА i-го типа в сист. с производством
-максимальный темп поступления ЛА i-го типа в сист. с производством – интенсивность ассигнований на развитие системы ЛА
– интенсивность ассигнований на развитие системы ЛА

 – годовая стоимость эксплуатации ЛА i-го вер-та
– годовая стоимость эксплуатации ЛА i-го вер-та – стоимость продажи ЛА i-го типа за рубеж
– стоимость продажи ЛА i-го типа за рубеж – интенсивность продажи ЛА i-го типа за рубеж
– интенсивность продажи ЛА i-го типа за рубеж – доля дохода от продажи ЛА за рубеж, которая выделяется на развитие СЛА (0≤
– доля дохода от продажи ЛА за рубеж, которая выделяется на развитие СЛА (0≤  )
)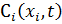 – стоимость создания ЛА i-го варианта
– стоимость создания ЛА i-го варианта - суммарная интенсивность выбытия ЛА i-го варианта из системы ЛА
- суммарная интенсивность выбытия ЛА i-го варианта из системы ЛА – темп выбытия ЛА i-го варианта из-за гибели и продажи за рубеж
– темп выбытия ЛА i-го варианта из-за гибели и продажи за рубеж – интенсивность гибели ЛА i-го варианта
– интенсивность гибели ЛА i-го варианта – управление, представляющее собой долю средств, выделяемую в момент t на производство ЛА i-го типа
– управление, представляющее собой долю средств, выделяемую в момент t на производство ЛА i-го типа ≤1,
≤1, 
 на производство ЛА i-го типа средств не выделяется, при
на производство ЛА i-го типа средств не выделяется, при  средства выделяются. Если на отрезке 0≤t≤T управляющие функции
средства выделяются. Если на отрезке 0≤t≤T управляющие функции  ,
,  (
(  – время завершения разработки ЛА i-го типа)
– время завершения разработки ЛА i-го типа)  позволяет найти траекторию развития СЛА i-го типа.
позволяет найти траекторию развития СЛА i-го типа.  даёт оптимальную траекторию(прогноз) развития системы ЛА
даёт оптимальную траекторию(прогноз) развития системы ЛА 
 определяются в результате решения вариационных задач
определяются в результате решения вариационных задач и скалярная композиция.
и скалярная композиция. 
 существующих и перспективных ЛА i-го типа
существующих и перспективных ЛА i-го типа  из которых на отрезке времени 0≤t≤T прогноз.дбсформирую БСЛА
из которых на отрезке времени 0≤t≤T прогноз.дбсформирую БСЛА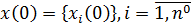


 ,
,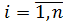 , обеспечивающие максимальное значение функционала в момент t=T .
, обеспечивающие максимальное значение функционала в момент t=T .
 ≥0, g(
≥0, g(