
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Задача аналитического конструирования оптимальных регуляторов.Предположим уравнения возмущенного движения системы имеют вид
Матрицы
где Требуется найти оптимальное (минимизирующее функционал 4.19) управление, являющееся функцией текущего состояния В соответствии с этим методом нужно найти функцию
В общем случае – это сложная задача, однако для линейных систем с квадратичным критерием оптимальности функцию Таким образом, для линейных систем задача сводится к отысканию функции
Тогда Минимизируя (4.23) по Так как Подставляя (4.24) в (4.23), получим Квадратичная форма (4.25) равна нулю при любых 
Интегрируя уравнение (4.26) в обратном направлении, получим
откуда с учетом симметричности матриц Замечание 1. В том случае, когда система (4.18) стационарна (матрицы A и B – числовые матрицы), матрицы
Замечание 2. Из выражения (4.24) следует, что для реализации оптимального управления необходима полная и точная информация о состоянии управляемого процесса
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 212. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (4.18)
(4.18) , размерности
, размерности  и
и  , соответственно, имеют в качестве своих элементов известные функции
, соответственно, имеют в качестве своих элементов известные функции  . Предполагается также, что состояние системы (4.18) в каждый момент времени
. Предполагается также, что состояние системы (4.18) в каждый момент времени  известно. В качестве критерия оптимальности рассматривается квадратичный функционал Больца
известно. В качестве критерия оптимальности рассматривается квадратичный функционал Больца , (4.19)
, (4.19) - симметричные неотрицательно определенные матрицы,
- симметричные неотрицательно определенные матрицы,  - положительно определенная матрица; *) - индекс транспортирования.
- положительно определенная матрица; *) - индекс транспортирования. . Для решения этой задачи можно воспользоваться принципом максимума, но наиболее короткий путь – метод динамического программирования.
. Для решения этой задачи можно воспользоваться принципом максимума, но наиболее короткий путь – метод динамического программирования. ,удовлетворяющего уравнению
,удовлетворяющего уравнению (4.20)
(4.20) (4.21) где
(4.21) где  - есть некоторая, пока неизвестная, квадратичная форма, удовлетворяющая в силу (4.16) конечному условию
- есть некоторая, пока неизвестная, квадратичная форма, удовлетворяющая в силу (4.16) конечному условию  (4.22)
(4.22)
 (4.23)
(4.23) получим
получим  или
или  (4.24)
(4.24)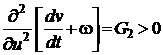 , то управление (4.24) действительно доставляет минимум выражению
, то управление (4.24) действительно доставляет минимум выражению  .
. (4.25)
(4.25) (4.26) с граничным условием (4.22).
(4.26) с граничным условием (4.22).
 следует, что
следует, что  .
. (рассматривается установившийся режим). Матрица
(рассматривается установившийся режим). Матрица  тоже числовая и удовлетворяет алгебраическому уравнению
тоже числовая и удовлетворяет алгебраическому уравнению