Метод деформируемого многогранника (метод Нелдера-Мида)

Метод Нелдера — Мида, также известный как метод деформируемого многогранника и симплекс-метод, — метод безусловной оптимизации функции от нескольких переменных, не использующий градиентов функции, а поэтому легко применим к негладким и/или зашумлённым функциям. В методе Нелдера и Мида минимизируется функция n независимых переменных с использованием n+1 вершин деформируемого многогранника в Eⁿ. Каждая вершина может быть идентифицирована вектором x. Вершина (точка) в Eⁿ, в которой значение f(x) максимально, проектируется через центр тяжести (центроид) оставшихся вершин. Улучшенные (более низкие) значения целевой функции находятся последовательной заменой точки с максимальным значением f(x) на более «хорошие точки», пока не будет найден минимум f(x).

Суть метода заключается в последовательном перемещении и деформировании симплекса вокруг точки экстремума. Предполагается, что серьёзных ограничений на область определения функции нет, то есть функция определена во всех встречающихся точках.

Параметрами метода являются: 1)коэффициент отражения α > 0, обычно выбирается равным 1. 2)коэффициент сжатия β > 0, обычно выбирается равным 0,5. 3) коэффициент растяжения γ > 0, обычно выбирается равным 2.

 Алгоритм метода (см вопрос 21)

Метод покоординатного спуска

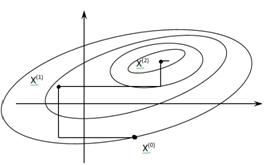При оптимизации по данному методу траектория поиска экстремума функции  выбирается в виде ломаной линии, отдельные отрезки которой параллельны координатным осям пространства оптимизируемых параметров . В случае n=2 можно на примере линий равного уровня, то есть геометрического места точек, в которых соблюдается условие 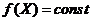, показать данную траекторию.

Опишем данный метод.

После выбора некоторого начального приближения ищется  при фиксированных значениях . Таким образом, движение из точки  происходит по прямой, параллельной оси  в сторону убывания функции . Затем поиск идет вдоль оси  из точки с координатами 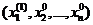, то есть ищется 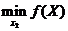. Описанная процедура последовательно повторяется для всех .

По завершению поиска по всем  получаем точку . Процесс поиска повторяется аналогично вышеизложенному, и в результате имеем точку 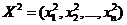 и так далее. Итерационный процесс поиска заканчивается, когда изменение аргумента X мало влияет на изменение функции , то есть выполняется следующее неравенство вида:

                                                                        (1.5),

где -заданная точность вычислений.

Примечание. При поиске минимума функции по направлению вдоль оси ,  переход от начальной точки  к точке  происходит в соответствии с формулой:

                                                                     (1.6),

где параметр  может принимать значение 1 или -1, а -величина шага в данном направлении. При отыскании  коэффициент  меняется от начального значения до минимально возможного .