
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Задача оптимальной фильтрации и ее решение методом КалманаДля оптимального управления по принципу обратной связи необходимо иметь полную информацию о состоянии системы. Однако измерению доступны лишь некоторые функции состояния или их комбинации. Кроме того, наблюдаемый сигнал содержит погрешности измерений. Задача получения наилучшей оценки состояния системы по результатам измерений – задача оптимальной фильтрации. Предположим, что динамический процесс описывается совокупностью дифференциальных уравнений Относительно свойств случайных процессов Калман предложил искатьуравнение фильтра в виде линейной системы на вход которой подается наблюдаемый сигнал Так как Тогда для определения искомых матриц 
Если теперь положить, что Чтобы убедиться в этом, достаточно взять математическое ожидание от выражений (5.67), (5.68)
Остается определить матрицу
Здесь Нетрудно показать, что минимизация производной критерия обеспечивает минимум и для самого критерия [6] Запишем выражение
Подставив в (5.72) выражение для Найдем Тогда Используем свойство дельта-функции: Аналогично можно найти Подставив полученные выражения для
Следующее тождество легко проверить, раскрыв в правой части скобки и использовав симметрию матрицы
С учетом тождества приведем уравнение (5.76) к виду:
В правой части (5.78) от коэффициента При этом последний член в уравнении (5.78) обращается в нульи уравнение приобретает вид с начальным значением Итак, можем записать уравнение фильтра
Уравнения (5.79), (5.80), (5.81) представляют собой уравнения фильтра Калмана-Бьюси. Система оценивания (фильтр) схематически представлена на рис. 16.
Для стационарной системы Запишем уравнения стационарного фильтра Калмана в следующем виде:
Один из часто используемых способов решения уравнения (5.84) (обычно с помощью ЦВМ) заключается в решении нестационарного уравнения (5.80) с соответствующими постоянными значениями коэффициентов, из которых составлены матрицыА, С, Q, R, и произвольной неотрицательно определенной матрицей начальных условий для Замечание 1. Важным свойством полученной ошибки является то, что она некоррелирована с ошибкой оценивания, [7] т.е. Замечание 2. Пусть теперь уравнение измерения имеет вид (5.62), а погрешность измерения отсутствует. В этом случае для получения оценки которая может быть представлена в виде (5.62) Замечание 3. Для управляемых систем, описываемых совокупностью уравнений с начальным условием
Система оценивания (фильтр) схематически представлена на рис. 17.
|
|||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 256. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
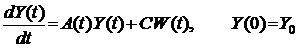 , (5.61) где
, (5.61) где  -
- 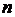 -мерный вектор состояния,
-мерный вектор состояния,  -
-  -мерный вектор возмущающих воздействий,
-мерный вектор возмущающих воздействий,  и
и  матрицы соответствующих размерностей. Пусть измерению поддается
матрицы соответствующих размерностей. Пусть измерению поддается  -мерный вектор некоторых комбинаций функций состояния (5.25)
-мерный вектор некоторых комбинаций функций состояния (5.25)  ,(5.62) где
,(5.62) где  - погрешность измерения.
- погрешность измерения. и начального состояния
и начального состояния  будет предполагать, что это случайные процессы типа белого шума, не корренированные друг с другом и начальным состоянием системы. Математически задача оптимальной фильтрации ставится как задача отыскания оценки
будет предполагать, что это случайные процессы типа белого шума, не корренированные друг с другом и начальным состоянием системы. Математически задача оптимальной фильтрации ставится как задача отыскания оценки  состояния системы (5.61)
состояния системы (5.61) 
 (5.63) где матрицы
(5.63) где матрицы  и
и  подлежат определению, т.е. структура фильтра задается, а параметры структуры и начальное состояние определяются из дополнительных условий.
подлежат определению, т.е. структура фильтра задается, а параметры структуры и начальное состояние определяются из дополнительных условий.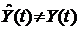 , то всегда будет ошибка оценки
, то всегда будет ошибка оценки  .
. можно использовать условие несмещенности оценки
можно использовать условие несмещенности оценки  (5.64) и условие ее оптимальности
(5.64) и условие ее оптимальности  , (5.65) где
, (5.65) где  - симметричная положительно определенная матрица. Для того, чтобы использовать условия (5.64) и (5.65) найдем уравнение для оценки оценивания. Вычитая (5.63) из (5.61) с учетом (5.62), получим
- симметричная положительно определенная матрица. Для того, чтобы использовать условия (5.64) и (5.65) найдем уравнение для оценки оценивания. Вычитая (5.63) из (5.61) с учетом (5.62), получим или
или .
. , (5.66) то уравнение для ошибки оценки
, (5.66) то уравнение для ошибки оценки  примет вид:
примет вид:  (5.67) с начальным условием
(5.67) с начальным условием  .(5.68) Из (5.67), (5.68) следует, что условие несмещенности оценки (5.64) будет выполнено, если положить
.(5.68) Из (5.67), (5.68) следует, что условие несмещенности оценки (5.64) будет выполнено, если положить  .(5.69)
.(5.69) . т.е. получили однородное линейное уравнение с нулевыми начальными условиями, откуда непосредственно следует, что
. т.е. получили однородное линейное уравнение с нулевыми начальными условиями, откуда непосредственно следует, что  для любого
для любого 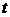 .
. . (5.70)
. (5.70)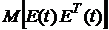 - корреляционная матрица ошибки оценивания (матрица вторых центральных моментов ошибок оценки компонент вектора состояния системы). Обозначим ее через
- корреляционная матрица ошибки оценивания (матрица вторых центральных моментов ошибок оценки компонент вектора состояния системы). Обозначим ее через  , тогда критерий оптимальности есть сумма диагональных элементов этой матрицы. В соответствие с условием локальной оптимальности будем искать оптимальное значение матрицы
, тогда критерий оптимальности есть сумма диагональных элементов этой матрицы. В соответствие с условием локальной оптимальности будем искать оптимальное значение матрицы  . (5.71)
. (5.71) , опуская для простоты время
, опуская для простоты время  . (5.72)
. (5.72) из (5.67) и соответствующее выражение для
из (5.67) и соответствующее выражение для  , получим:
, получим:  (5.73)
(5.73) , для чего запишем уравнение Коши для (5.67):
, для чего запишем уравнение Коши для (5.67):  , где
, где 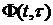 - весовая матричная функция.
- весовая матричная функция. .
.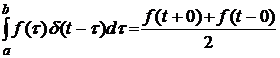 , если
, если  имеет разрыв в точке
имеет разрыв в точке  . Поскольку
. Поскольку  то
то  . (5.74)
. (5.74) :
:  . (5.75)
. (5.75) и соответственно транспонированные выражения для
и соответственно транспонированные выражения для  в (5.73) получим:
в (5.73) получим: (5.76)
(5.76)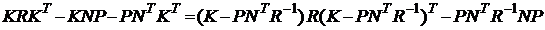 . (5.77)
. (5.77) (5.78)
(5.78) (5.79)
(5.79) (5.80)
(5.80) .
. . (5.81)
. (5.81) Следует отметить, что уравнение фильтра и его параметры не зависят от матрицы
Следует отметить, что уравнение фильтра и его параметры не зависят от матрицы  при стационарном возмущающем воздействии
при стационарном возмущающем воздействии  и стационарном шуме измерителя
и стационарном шуме измерителя  после окончания переходных процессов матричный коэффициент усиления в фильтре Калмана становится постоянным
после окончания переходных процессов матричный коэффициент усиления в фильтре Калмана становится постоянным  , а уравнение Риккати (5.80) вырождается в алгебраическое. При этом процесс
, а уравнение Риккати (5.80) вырождается в алгебраическое. При этом процесс  .
. ; (5.82)
; (5.82)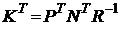 ; (5.83)
; (5.83) . (5.84)
. (5.84) в текущем времени до тех пор, пока полученное решение не достигнет постоянного установившегося значения. Это окончательное значение принимается за искомое решение уравнения (5.84). Такой способ решения удобен тем, что алгоритмы решения дифференциальных уравнений, как правило, эффективнее алгоритмов решения нелинейных алгебраических уравнений.
в текущем времени до тех пор, пока полученное решение не достигнет постоянного установившегося значения. Это окончательное значение принимается за искомое решение уравнения (5.84). Такой способ решения удобен тем, что алгоритмы решения дифференциальных уравнений, как правило, эффективнее алгоритмов решения нелинейных алгебраических уравнений. .
. наблюдаемого сигнала
наблюдаемого сигнала  ,
, . где
. где  . Далее процедура вывода уравнений фильтра совпадает с выше изложенной.
. Далее процедура вывода уравнений фильтра совпадает с выше изложенной. . Уравнение фильтра может быть получено аналогично. В этом случае уравнение фильтра будет иметь вид
. Уравнение фильтра может быть получено аналогично. В этом случае уравнение фильтра будет иметь вид 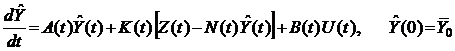 , (5.85) где матрица
, (5.85) где матрица  , а корреляционная матрица
, а корреляционная матрица  (5.86)
(5.86) .
.