
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Принципы методов численного поиска минимума функции многих переменныхМногие задачи оптимизации, какими бы способами они ни решались в конце концов сводятся к задаче минимизации функции многих переменных В качестве Точка Методы безусловной оптимизации базируются на результатах, известных из математического анализа, в частности на необходимых и достаточных условиях минимума функции. 1. Если в точке 1) решается система уравнений (3) и находятся стационарные точки; 2) используются достаточные условия, находятся точки локального минимума и глобального. Общие принципы 1) Для численного решения задач безусловной оптимизации, используются итерационные процедуры  т.е. выбор параметра на Простейшие процедуры типа (4) можно представить в виде:
где 2) Величина шага выбирается так, чтобы выполнилось условие Практически все методы оптимизации можно разделять условно на две группы. 1) Прямые методы оптимизации, в которых на каждом шаге вычисляется только значение целевой функции. 2) Методы, использующие производные целевой функции. Прямые методы. 1. Метод перебора. Ограничимся случаем одномерной оптимизации унимодальных функций. Функция 1) на отрезке 2) на отрезке В этом случае отрезок Для обеспечения необходимой точности нужно выбрать число деления участков 2. Метод поразрядного поиска. Используются некоторые возможности улучшения метода перебора. Во-первых, если оказывается, что Прямые методы 1. Минимизации по правильному симплексу (ПС). ПС в 2. Метод покоординатного спуска. 3. Метод случайного поиска Методы, использующие производные целевой функции. Пусть Метод градиентного спуска Здесь Метод наискорейшего спуска.Здесь тоже Многомерная минимизация при наличии ограничений.Задача математического программирования. Соотношение (1) – (3) – задача математического программирования. 1. Задача линейного программирования, когда все функции линейны и 2. Задачи нелинейного программирования, когда хотя бы одна функция – нелинейная. 2.1. Задача на условный экстремум, когда отсутствуют условия (2). 2.2. Задача выпуклого программирования, когда все функции выпуклых и отсутствует условия (3). Напомним, что функция, заданная на отрезке |
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 247. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (1)
(1) 
 могут быть проектные параметры приборов и технологических процессов, элементы матриц оптимизируемых функционалов, начальные условия для множителей Лагранжа и др. Здесь
могут быть проектные параметры приборов и технологических процессов, элементы матриц оптимизируемых функционалов, начальные условия для множителей Лагранжа и др. Здесь  – допустимое значение множества изменения параметров
– допустимое значение множества изменения параметров  . Точка
. Точка  называется точкой глобального минимума
называется точкой глобального минимума  , если для всех
, если для всех  выполняется неравенство
выполняется неравенство  для всех
для всех  называется точкой локального минимума функции
называется точкой локального минимума функции  - окрестность точки
- окрестность точки 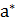 :
:  (
( 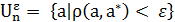 , такая, что
, такая, что  . Если допустимое множество
. Если допустимое множество  , то говорят о задаче безусловной оптимизации
, то говорят о задаче безусловной оптимизации 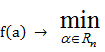 (2)
(2) функция дифференцируема и достигает локального минимума, то
функция дифференцируема и достигает локального минимума, то  или
или 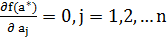 (3) Точки, в которых выполняются условия (3), называются точками стационарности функции
(3) Точки, в которых выполняются условия (3), называются точками стационарности функции  . 2. Если в стационарной точке
. 2. Если в стационарной точке  положительно определена, то
положительно определена, то  – мерной оптимизации
– мерной оптимизации (4)
(4) шаге зависит от информации о предыдущих шагах.
шаге зависит от информации о предыдущих шагах. (5)
(5) – направление движения из точки
– направление движения из точки  в точку
в точку  , число
, число  – величина шага.
– величина шага.
 называется унимодальной на отрезке
называется унимодальной на отрезке  , если она непрерывна на
, если она непрерывна на  такие, что:
такие, что: функция
функция  функция
функция 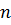 равных частей точками
равных частей точками  . Вычисляются
. Вычисляются 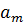 минимального значения, т.е.
минимального значения, т.е.  , т.е.
, т.е.  . Понятно, что погрешность определения
. Понятно, что погрешность определения 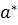 не превосходит величины
не превосходит величины 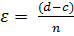 .
. .
. , то не нужно вычислять
, то не нужно вычислять  и т.д. Во-вторых, разумно сначала определить
и т.д. Во-вторых, разумно сначала определить  –мерной оптимизации. Остановимся сначала на вычислительных процедурах вида (5),в которых выбор нового приближения к точке минимума определяется сравнением значений функций в нескольких точках пространства
–мерной оптимизации. Остановимся сначала на вычислительных процедурах вида (5),в которых выбор нового приближения к точке минимума определяется сравнением значений функций в нескольких точках пространства  .
.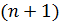 равноудаленных друг от друга точек (вершин симплекса). Отрезок, соединяющий 2 вершины – ребро. В
равноудаленных друг от друга точек (вершин симплекса). Отрезок, соединяющий 2 вершины – ребро. В 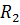 ПС – равносторонний треугольник в
ПС – равносторонний треугольник в  – правильный тетраэдр.
– правильный тетраэдр. ,где
,где  – величина шага,
– величина шага,  - некоторая реализация
- некоторая реализация  – дифференцируемая функция в
– дифференцируемая функция в  где направление убывания
где направление убывания 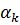 выбирается так, что
выбирается так, что  .
.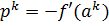 , а
, а  находится в результате одномерной минимизации
находится в результате одномерной минимизации  , где
, где 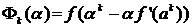

 .
. называется выпуклой на отрезке, если для всех
называется выпуклой на отрезке, если для всех  и
и  , принадлежащих отрезку и произвольного числа
, принадлежащих отрезку и произвольного числа  выполняется неравенство
выполняется неравенство  . Другое определение: Для выпуклости
. Другое определение: Для выпуклости  на отрезке
на отрезке  .
.