
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Принцип оптимальности Беллмана.Рассмотрим систему и функционал Применим принцип оптимальности к решению вариационной задачи (4.1), (4.2). Для этого сначала рассмотрим функционал Если Интервал (t, T) разделим на два интервала (t, t+ dt) и (t + dt,T) и выражение (4.8) запишем в виде: Обозначим: где Хотя функция
Учитывая, что получим основное уравнение метода динамического программирования:
Это соотношение состоит из двух утверждений: 1. выражение  2. выражение Если Здесь Подставляя (4.13) в (4.12) получим уравнение Р.Беллмана: Это уравнение в частных производных относительно В случае бесконечного интервала при Уравнение (4.12) сохраняет силу, функция v в момент
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 238. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (4.1)
(4.1)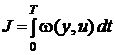 (4.2) который требуется минимизировать. Правый конец фазовых координат является свободным. Наряду с этой вариационной задачей рассмотрим вспомогательную, когда процесс рассматривается в интервале
(4.2) который требуется минимизировать. Правый конец фазовых координат является свободным. Наряду с этой вариационной задачей рассмотрим вспомогательную, когда процесс рассматривается в интервале  и минимизируется функционал
и минимизируется функционал  . (4.3)
. (4.3) (4.3). Наименьшее значение его при связях (4.1) обозначим:
(4.3). Наименьшее значение его при связях (4.1) обозначим: 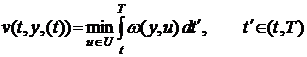 . (4.8)
. (4.8) - оптимальное управление, то
- оптимальное управление, то  . Оптимальное управление
. Оптимальное управление  зависит от начального состояния y(t) в момент (t). Следовательно, v является функцией от y и t: v = v(y, t), а от управления u и его вариаций функция v = v(y, t) не зависит. Она вполне определяется значениями y, t .
зависит от начального состояния y(t) в момент (t). Следовательно, v является функцией от y и t: v = v(y, t), а от управления u и его вариаций функция v = v(y, t) не зависит. Она вполне определяется значениями y, t . . Согласно принципу оптимальности последний участок также является оптимальным:
. Согласно принципу оптимальности последний участок также является оптимальным:  (4.9)
(4.9) , (4.10)
, (4.10) - приращение вектора фазовых координат за время
- приращение вектора фазовых координат за время  . Оно определяется согласно уравнениям движения (4.1). Подставляя
. Оно определяется согласно уравнениям движения (4.1). Подставляя  из (4.10) в равенство (4.9), получим:
из (4.10) в равенство (4.9), получим:  .
. . Значение приращения
. Значение приращения  . Но
. Но 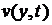 не зависит от управления в интервале
не зависит от управления в интервале  .
. ;
;  ,
, . (4.11)
. (4.11) достигает минимума. Это утверждение служит для определения оптимального управления
достигает минимума. Это утверждение служит для определения оптимального управления  ;
; .
. (4.12)
(4.12) зависит от управления по определению, функция же
зависит от управления по определению, функция же 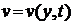 не зависит от него. Тем не менее, производная
не зависит от него. Тем не менее, производная  от управления зависит. В этом можно убедиться, если ее представить в виде
от управления зависит. В этом можно убедиться, если ее представить в виде  и
и  заменить согласно системе (4.1):
заменить согласно системе (4.1): 
 . (4.13)
. (4.13) . (4.14)
. (4.14) , которое после подстановки
, которое после подстановки  становится нелинейным. Согласно определению v (4.8) при
становится нелинейным. Согласно определению v (4.8) при  должно выполняться конечное условие
должно выполняться конечное условие  .
. процесс должен быть асимптотически устойчивым, т.е.
процесс должен быть асимптотически устойчивым, т.е.  . В том случае, когда рассматривается функционал Больца
. В том случае, когда рассматривается функционал Больца  (4.15)
(4.15) . (4.16)
. (4.16)