
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Не градиентные методы поиска минимума функции многих переменных.Задачи минимизации функции многихпеременных методами, не требующими вычисления градиента функции. К ним относятся метод покоординатного спуска, метод деформированного многогранника. Данная задача формулируется как задача безусловной оптимизации, сутью которой является поиск минимума функции многих переменных на всем пространстве соответствующей размерности. Функцию многих переменных Рассмотрим основные методы решения задач безусловной минимизации вида: Если функция Однако аналитически решить систему уравнений (1.2) не всегда возможно. Кроме того, функция В этих методах, после задания начальной точки  Новая точка Постановка задачи. Дана функция y=f(X) . Требуется найти минимум функции, используя метод покоординатного спуска или метод деформированного многогранника. Метод покоординатного спуска
Опишем данный метод. После выбора некоторого начального приближения По завершению поиска по всем
где Примечание. При поиске минимума функции где параметр Алгоритм метода покоординатного спуска. (см. вопрос 20) |
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 255. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
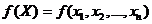 будем рассматривать как функцию, заданную в точках Xn-мерного эвклидова пространства En.
будем рассматривать как функцию, заданную в точках Xn-мерного эвклидова пространства En.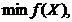 где
где  (1.1.)
(1.1.)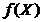 дважды дифференцируема, то данную задачу можно решить аналитически, используя необходимые и достаточные условия безусловного экстремума. Записав необходимые условия:
дважды дифференцируема, то данную задачу можно решить аналитически, используя необходимые и достаточные условия безусловного экстремума. Записав необходимые условия:  или
или 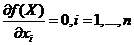 (1.2) находим все стационарные точки функции
(1.2) находим все стационарные точки функции  положительно определена. Сравнивая значения в этих точках, находим точку глобально минимума.
положительно определена. Сравнивая значения в этих точках, находим точку глобально минимума.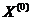 последовательно ищутся точки
последовательно ищутся точки 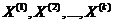 такие, чтобы выполнялось неравенство вида:
такие, чтобы выполнялось неравенство вида: 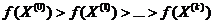 (1.3)
(1.3)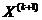 ищется с помощью итерационной процедуры вида:
ищется с помощью итерационной процедуры вида: 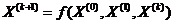 (1.4),в которой выбор нового приближения к точке минимума определяется сравнением значений функции
(1.4),в которой выбор нового приближения к точке минимума определяется сравнением значений функции 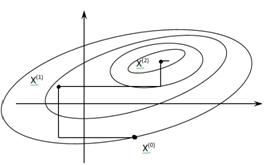 При оптимизации по данному методу траектория поиска экстремума функции
При оптимизации по данному методу траектория поиска экстремума функции  выбирается в виде ломаной линии, отдельные отрезки которой параллельны координатным осям пространства оптимизируемых параметров
выбирается в виде ломаной линии, отдельные отрезки которой параллельны координатным осям пространства оптимизируемых параметров 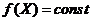 , показать данную траекторию.
, показать данную траекторию. ищется
ищется  при фиксированных значениях
при фиксированных значениях  . Таким образом, движение из точки
. Таким образом, движение из точки  происходит по прямой, параллельной оси
происходит по прямой, параллельной оси  в сторону убывания функции
в сторону убывания функции  . Затем поиск идет вдоль оси
. Затем поиск идет вдоль оси  из точки с координатами
из точки с координатами 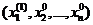 , то есть ищется
, то есть ищется 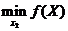 . Описанная процедура последовательно повторяется для всех
. Описанная процедура последовательно повторяется для всех  .
. получаем точку
получаем точку  . Процесс поиска повторяется аналогично вышеизложенному, и в результате имеем точку
. Процесс поиска повторяется аналогично вышеизложенному, и в результате имеем точку 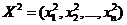 и так далее. Итерационный процесс поиска заканчивается, когда изменение аргумента X мало влияет на изменение функции
и так далее. Итерационный процесс поиска заканчивается, когда изменение аргумента X мало влияет на изменение функции  (1.5),
(1.5), -заданная точность вычислений.
-заданная точность вычислений. ,
,  переход от начальной точки
переход от начальной точки  к точке
к точке  происходит в соответствии с формулой:
происходит в соответствии с формулой: (1.6),
(1.6), может принимать значение 1 или -1, а
может принимать значение 1 или -1, а  -величина шага в данном направлении. При отыскании
-величина шага в данном направлении. При отыскании  коэффициент
коэффициент  до минимально возможного
до минимально возможного  .
.