
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Условный экстремум, виды связей, методы решенияПри решении прикладных задач при принятии того или иного решения, в том числе оптимального, всегда приходится учитывать совокупность ограничений по энергопотреблению, быстродействию, точности, (текущей или конечной), надежности и т.п. Эти ограничения всегда будут накладывать ограничения на выбор допустимых вариаций. Поиск экстремума функционала при наличии дополнительных ограничений (связей), называется задачей на условный экстремум. Обычно различают связи трех типов: а) голономные связи – связи, не содержащие производных искомых функций б) неголономные связи – связи, содержащие производные искомых функций в) изопериметрические (интегральные связи) Вариационные задачи на условный экстремум при голономных и неголономных связях можно (теоретически) решить методом исключения зависимых переменных. Тогда задача на условный экстремум сводится к задаче на безусловный. Однако такой подход практически неприменим ввиду сложности процедур исключения зависимых переменных. Поэтому наибольшее распространение получил метод множителей Лагранжа. Рассмотрим применение этого метода в задаче минимизации функционала
граничные условия будем считать заданными. В соответствие с методом Лагранжа вводится вспомогательный функционал
Однако в этом случае нельзя воспользоваться основной леммой вариационного исчисления, так как 
В последнем выражении
Таким образом, для определения n+m функций
Уравнения (1.31) называются уравнениями Эйлера-Лагранжа. Если граничные условия не заданы, система уравнений (1.31) дополняется условиями трансверсальности типа (1.25), в которых вместо F необходимо подставить H.
В случае неголономных связей вариационные задачи решаются аналогично.
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 289. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 ;
; ;
; .
. при наличии связей
при наличии связей  , (1.29)
, (1.29) , где
, где  - неопределенные пока множители Лагранжа. На связях
- неопределенные пока множители Лагранжа. На связях  и
и  и функционалы
и функционалы  и
и  ведут себя одинаково, т.е. экстремум
ведут себя одинаково, т.е. экстремум  удовлетворяют уравнениям связей (1.29), независимо от
удовлетворяют уравнениям связей (1.29), независимо от  .При заданных граничных условиях, как и ранее, получим
.При заданных граничных условиях, как и ранее, получим 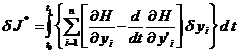 .
. - не является независимыми. Воспользуемся свободой выбора множителей Лагранжа и выберем
- не является независимыми. Воспользуемся свободой выбора множителей Лагранжа и выберем  уравнений
уравнений , тогда
, тогда  .
.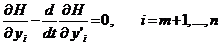 .
. и
и 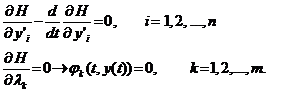 (1.31)
(1.31)