
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Решение задачи при изопериметрических условиях.Рассмотрим задачу нахождения экстремума функционала
Такие связи не накладывают ограничений на вариации функций Вариационная задача с ограничениями (1.32) может быть сведена к задаче с неголономными связями, если ввести новые переменные Из (1.33) следует, что вектор-функция
Введем функции
Тогда Уравнения Эйлера-Лагранжа будут иметь вид:
Так как Таким образом, множители Лагранжа в вариационной задаче с изопериметрическими условиями являются постоянными величинами, для определения которых имеется система (1.32). При этом система уравнений Эйлера-Лагранжа (1.36) может быть записана в виде
Система управлений (1.37) должна решаться совместно с условиями (1.32) и граничными условиями, вытекающими из условия трансверсальности.
Необходимые и достаточные условия относительного минимума Рассмотрим некоторый функционал
где На экстремали Рассмотрим такую достаточно малую окрестность экстремали, что 
Тогда знаки приращения Если
Условие Лежандра Рассмотрим задачу нахождения экстремума простейшего функционала
с закрепленными концами. Докажем, что для достижения относительного минимума необходимо Неравенства (1.42) и (1.43) называются условиями Лежандра. Используя формулу Тейлора, найдем
Предполагается, что отброшенные нелинейные члены более высокого порядка малости, чем Используя равенства
для второй вариации
Введем обозначения Тогда Убедимся, что для достижения минимума Пусть Тогда при Но
доказывается необходимость
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 303. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 при наличии изопериметрических связей
при наличии изопериметрических связей  (1.32) где
(1.32) где  - заданные постоянные величины.
- заданные постоянные величины. в текущий момент времени, они являются интегральными, поэтому число связей может быть и больше, чем число функций, т.е. m><n.
в текущий момент времени, они являются интегральными, поэтому число связей может быть и больше, чем число функций, т.е. m><n. . (1.33)
. (1.33)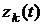 удовлетворяет системе уравнений
удовлетворяет системе уравнений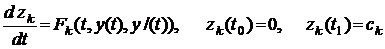 . (1.34)
. (1.34) и
и 
 .
.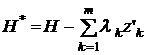 и задача минимизации функционала
и задача минимизации функционала  сводится к задаче минимизации функционала
сводится к задаче минимизации функционала 
 (1.35)
(1.35)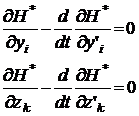 (1.36)
(1.36) , то
, то  и
и  . Значит
. Значит  .
. . (1.37)
. (1.37) , где
, где 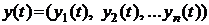 , и приращение его представим в виде
, и приращение его представим в виде ,
, - вторая вариация функционала,
- вторая вариация функционала,  - величина более высокого порядка малости, чем
- величина более высокого порядка малости, чем  при
при  и
и  при
при  . Безусловно, предполагается способ приближения
. Безусловно, предполагается способ приближения  к нулю заданным.
к нулю заданным. , тогда
, тогда  .
. .
. и второй вариации
и второй вариации  , то
, то  , и если
, и если  . (1.40)
. (1.40) (1.41)
(1.41)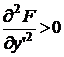 , (1.42) а для максимума – условие
, (1.42) а для максимума – условие  .(1.43)
.(1.43)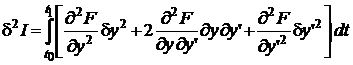 .
.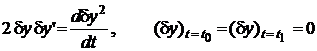 ;
; ,
, .
.
 .
.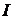 , если он существует, необходимо
, если он существует, необходимо  . Для этого покажем, что если
. Для этого покажем, что если 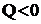 , то всегда можно найти такую функцию
, то всегда можно найти такую функцию  , т.е. всегда можно построить такую кривую сравнения, что знак
, т.е. всегда можно построить такую кривую сравнения, что знак  .
. , т.е. достигается минимум функционала, и допустим, что в некоторой точке
, т.е. достигается минимум функционала, и допустим, что в некоторой точке  выполняется неравенство
выполняется неравенство  . Тогда
. Тогда  в силу непрерывности Q по t в некоторой окрестности
в силу непрерывности Q по t в некоторой окрестности  этой точки
этой точки  . Зададимся (рис. 9):
. Зададимся (рис. 9):  ;
;  .
.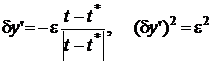
 , и, следовательно, будем иметь:
, и, следовательно, будем иметь:  .
. , поэтому при достаточно малом, но положительном
, поэтому при достаточно малом, но положительном 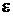 получим:
получим: .
. Это противоречит
Это противоречит  . Следовательно, для достижения относительного и слабого экстремума необходимо, чтобы
. Следовательно, для достижения относительного и слабого экстремума необходимо, чтобы  . Аналогично
. Аналогично для достижения максимума. Эти необходимые условия максимума и минимума более сильны, чем уравнения Эйлера, которые не могут различать максимума от минимума. Условия Лежандра используются совместно с уравнениями Эйлера, и при помощи их различают максимум и минимум.
для достижения максимума. Эти необходимые условия максимума и минимума более сильны, чем уравнения Эйлера, которые не могут различать максимума от минимума. Условия Лежандра используются совместно с уравнениями Эйлера, и при помощи их различают максимум и минимум.