
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Уравнение Эйлера (для заданного функционала)
называется уравнением Эйлера. Уравнению Эйлера удовлетворяют кривые, доставляющие как относительный минимум, так и относительный максимум функционалу Учитывая, что
То есть уравнение Эйлера – это дифференциальное уравнение второго порядка относительно Рассмотрим некоторые частные случаи уравнения Эйлера. 1. Функция
Откуда следует
Интегрируя его, найдем 1. В функцию
Условие трансверсальности ( для конкретного случая).
Полученное условие может быть использовано для определения оптимальных значений координат граничных точек. Оно называется условием трансверсальности и используется совместно с уравнением Эйлера (см. вопрос. 5) . Рассмотрим некоторые частные условия трансверсальности.  1. Точки A и Bзаданы. В этом случае 2. Координаты 3. Точка A задана, а координаты точки B связаны зависимостью и из условия трансверсальности получим недостающее условие В том случае, когда y(t) – n – мерный вектор достаточно гладких функций, искомая экстремаль удовлетворяет системе уравнений Эйлера а условие трансверсальности имеет вид: Из условия трансверсальности можно получить систему соотношений для определения граничных значений
тогда соответствующая система уравнений в вариациях будет иметь вид:
Используя полученную систему линейных алгебраических уравнений (1.27), можно выразить |
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 265. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , (1.18)
, (1.18) , поэтому для идентификации экстремума необходимы дополнительные исследования.
, поэтому для идентификации экстремума необходимы дополнительные исследования. , уравнение Эйлера можно представить в виде
, уравнение Эйлера можно представить в виде .
. , его общее решение содержит две произвольные постоянные
, его общее решение содержит две произвольные постоянные  и
и 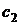
 , для нахождения которых используются условия прохождения искомой экстремали через заданные точки
, для нахождения которых используются условия прохождения искомой экстремали через заданные точки 
 и
и  . Таким образом, решение задачи построения экстремали сводится к краевой задаче (или двухточечной), которая существенно отличается от задачи Коши, где решение удовлетворяет только начальным условиям. Двухточечная задача может и не иметь решения, когда задача Коши решение имеет.
. Таким образом, решение задачи построения экстремали сводится к краевой задаче (или двухточечной), которая существенно отличается от задачи Коши, где решение удовлетворяет только начальным условиям. Двухточечная задача может и не иметь решения, когда задача Коши решение имеет. не содержит
не содержит  , т.е.
, т.е.  . При этом
. При этом  , и уравнение Эйлера запишется в виде
, и уравнение Эйлера запишется в виде .
. , где
, где  , получим:
, получим: .
. ,
, 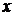 и
и  , и уравнение Эйлера преобразуется к виду
, и уравнение Эйлера преобразуется к виду  , или
, или  . В этом случае
. В этом случае  . Экстремали представляют прямые линии.
. Экстремали представляют прямые линии. (1.23)
(1.23)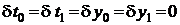 , условие (1.23) выполняется тождественно и дополнительной информации не дает.
, условие (1.23) выполняется тождественно и дополнительной информации не дает. и
и 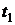 , заданы, а
, заданы, а  и
и  произвольны. В этом случае
произвольны. В этом случае  и из условия трансверсальности получаем дополнительно два условия для определения
и из условия трансверсальности получаем дополнительно два условия для определения 
 . В этом случае
. В этом случае  , а вариации
, а вариации  и
и  связаны зависимостью
связаны зависимостью  ,
, .
. (1.24)
(1.24) (1.25)
(1.25) параметров
параметров  . В общем случае эти параметры могут быть связаны условиями
. В общем случае эти параметры могут быть связаны условиями , (1.26)
, (1.26) (1.27)
(1.27) зависимых переменных через
зависимых переменных через  независимых переменных и из условия трансверсальности (1.25) получить
независимых переменных и из условия трансверсальности (1.25) получить  переменных (координат граничных точек).
переменных (координат граничных точек).