
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Движение частицы в области низкого и высокого потенциального порога. Коэффициент отражения частицы от порога и коэффициент прохождения через порог.Потенциальным порогом ( потенциальной стенкой ) называют силовое поле, в котором потенциальная энергия частицы имеет вид
Пусть слева на порог налетает частица с полной энергией Е . На языке квантовой теории это означает, что на порог слева «падает» дебройлевская волна
Чтобы удовлетворить граничным условиям дляΨ и Задача состоит в том, чтобы сначала найти амплитуды отражённой и падающей волн, а затем коэффициенты отражения R и пропускания D . Уравнение Шрёдингера для частицы в данном силовом поле имеет вид: в области I( x < 0 ) в области II( x > 0 ) 1).Низкий порог ( Е > U0 ) Общее решение уравнения Шрёдингера имеет вид: Будем считать, что падающая волна характеризуется амплитудой А1 , причём вещественной, а отражённая – амплитудой В1 . В области II( x > 0) имеется только проходящая волна, поэтому В2 = 0 . Из условия непрерывности Ψ и Тогда Для определения коэффициентов R и D вводят понятие плотности потока вероятностиj, вектор которого определяется через волновую функцию следующим образом: В соответствии с видом Ψ-функции для падающей, отражённой и прошедшей волн имеем: jпад~ k1A12 , jотр~ k1B12 и jпрош ~ k2A22 Теперь можно записать для коэффициента отражения
для коэффициента пропускания Видно, что R + D = 1 , что и должно быть по определению. Коэффициенты R и D не зависят от направления движения частицы: слева направо или наоборот.  В классическом случае при E > U0 должно быть R = 0. Эффектнадбарьерного отражения( R > O ) является чисто квантовым и объясняется наличием у частицы волновых свойств. 2). Высокий порог ( E < U0 ).
В этом случае величины комплексно-сопряжённые. Таким образом, отражение будет полным, а D = 0. Но волновая функция при x > 0 не обращается в нуль, т.е. микрочастицы могут проникать в области, которые для макроскопических частиц недоступны. Плотность вероятности нахождения частицы в области II определяется выражением Для электрона с (U0 – E) = 1 эВ вероятность нахождения на расстоянии от порога сравнимым с размерами атома ( х = 10-10 м ) достаточно велика, а на расстоянии в 10 раз большем ( х = 10-9 м ) ничтожно мала. Отражение хотя и является полным (R = 1) не обязательно происходит на самом пороге. Частица может проникнуть в область II , а затем выйти из неё ( аналогично полному внутреннему отражению в оптике).
Прохождение частицы через прямоугольный потенциальный барьер и коэффициент его прохождения. Приближенное выражение для коэффициента прохождения через достаточно широкий и высокий барьер произвольной формы. Рассмотрим одномерный прямоугольный потенциальный барьер Частица движется слева направо. Слева от барьера имеем падающую и отраженную волну, а за барьером только прошедшую волну. Уравнение Шрёдингера для областей I, II и III имеет вид: Где Волновые функции, являющиеся решением этих уравнений Из решения этой системы уравнений получают, применив некоторые упрощающие допущения, выражение для коэффициента прозрачности Dпрямоугольного барьера Для потенциального барьера произвольной формы Пределы интегрирования х1 и х2 определяют из решения уравнения U( x ) = E . Частица массой т0 падает на прямоугольный потенциальный барьер высотой U0 и шириной а . Энергия частицыЕбольше высоты барьера. В этом случае решение системы уравнений Шрёдингера для трёх областей: I – ( x <0 ), II – ( 0 < x < a ), III – ( x > a )даёт следующие значения для коэффициента прохождения D . Частица беспрепятственно проходит над таким барьером ( D = 1) при значениях энергии равных При других значениях энергии существует отличная от нуля вероятность отражения частицы от барьера.
Квантовый гармонический осциллятор (одномерный). Закон квантования энергии гармонического осциллятора (результаты решения уравнения Шрёдингера) и следствия из него: эквидистантные уровни энергии, правило отбора, нулевые колебания. Как известно, гармоническим осциллятором называется система, способная совершать гармонические колебания. В физике модель гармонического осциллятора играет важную роль, особенно при исследовании малых колебаний систем около положения устойчивого равновесия. Примером таких колебаний в квантовой механике являются колебания атомов в твердых телах, молекулах и т.д. Рассмотрим одномерный гармонический осциллятор, совершающий колебания вдоль оси
где Рассмотрим сначала поведение классического гармонического осциллятора. Пусть частица с полной энергией
В квантовой механике для решения задачи о гармоническом осцилляторе нужно решить уравнение Шредингера с потенциальной энергией
Вводя величины
и переходя к новой безразмерной переменной
Анализ показывает, что волновые функции, являющиеся решением уравнения, будут непрерывными и конечными не при всех значениях параметра
Выражая, согласно (4.79), энергию осциллятора
Это соотношение и определяет закон квантования энергии гармонического осциллятора. Отметим, что энергетические уровни гармонического осциллятора, в отличие, например, от случая прямоугольной потенциальной ямы, являются эквидистантными, т.е. расположены на одинаковом энергетическом расстоянии
Еще одной важной особенностью спектра является наличие так называемых нулевых колебаний - колебаний с энергией Нулевые колебания играют в физике весьма важную роль, в частности они обусловливают отсутствие кристаллизации жидкого гелия при нормальном давлении даже при абсолютном нуле температур. Велика роль нулевых колебаний и в объяснении природы сил молекулярных взаимодействий, физических особенностей поверхностного натяжения, адсорбции и других молекулярных явлений. На эксперименте наличие нулевых колебаний наблюдается, в частности, в опытах по рассеянию света кристаллами при низких температурах. Условия, которые определяют изменение квантовых чисел при разрешенных переходах системы из одного состояния в другое, называются правилами отбора. Таким образом, правила отбора, характеризующие испускание и поглощение электромагнитного излучения гармоническим осциллятором 25. Квантовомеханическая модель атома водорода. Уравнение Шредингера для атома водорода и результаты его решения: спектр собственных значений энергии, модуля и z-проекции момента импульса. Квантовые числа. Коммутатор оператора Гамильтона с оператором квадрата момента импульса и z-проекции момента импульса. Квантово-механическая модель атома предполагает, что в ядре атома находятся не имеющие заряд нейтроны и положительно заряженные протоны. Вокруг него расположены отрицательно заряженные электроны. Но по квантовой механике, электроны не движутся по заранее заданным определенным траекториям.Так, в 1927 году В. Гейзенберг озвучил принцип неопределенности, по которому представляется невозможным точное определение координаты частицы и ее скорости или импульса. Химические свойства электронов определены их оболочкой. В таблице Менделеева атомы расположены согласно электрическим зарядам ядер (речь идет о количестве протонов), нейтроны при этом не влияют на химические свойства. Квантово-механическая модель атома доказала, что основная его масса приходится на ядро, а доля электронов при этом остается незначительной. Она измеряется в атомных единицах массы, которая равна 1/12 массы атома изотопа углерода С12. Применим уравнение Шредингера к электрону, находящемуся в атоме водорода. Решение задачи об энергетических уровнях электрона для водорода, а также водородоподобных систем сводится к задаче о движении электрона в кулоновском поле ядра. Потенциальная энергия взаимодействия электрона с ядром, обладающим зарядом Ze(для атома водорода Z = 1), определяется выражением
Электрон в атоме находится в потенциальной яме, края которой имеют форму гиперболы Очевидно, что решение этой задачи должно быть подобно решению задачи, когда частица находилась в бесконечно глубокой одномерной потенциальной яме с прямоугольными краями. Так как электрическое поле – центрально-симметрично, то для решения этого уравнения воспользуемся сферической системой с координатами (r, θ, φ),
которые связаны с декартовыми координатами, как это следует из, соотношениями: x = r sin θ cos φ; y = r sin θ sin φ; z = r cosθ .
Строгое решение уравнения в соответствии с теорией дифференциальных уравнений дает следующие результаты. Электрон в атоме обладает не произвольным значением энергии, а набором определенных отрицательных дискретных значений En:
где n – главное квантовое число, принимающее значения 1,2,3.…,∞. Из следует, что именно главное квантовое число определяет энергию электрона в атоме: En~ Оказывается, что одному и тому же значению энергии электрона соответствует несколько различных состояний с разными волновыми функциями, соответствующими различным типам движения электрона. Эти типы движения различаются разными значениями орбитального момента импульса и его проекцией на физически выделенное направление Z, совпадающее с направлением вектора напряженности внешнего магнитного поля. В квантовой механике доказывается, что уравнению Шредингера удовлетворяют собственные функции Ψn l m s , определяемые набором четырех квантовых чисел: главного n, орбитального l, магнитногоm и спинового ms. Момент импульса частицы Оператор Гамильтона:
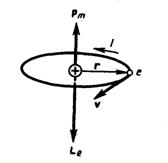
Гиромагнитное отношение орбитальных моментов электрона. Соотношение между операторами орбитального магнитного момента и орбитального момента импульса электрона. Квантование орбитального магнитного момента электрона в атоме водорода. Магнетон Бора. Рассматривая действие магнитного поля на проводники с током и на движущиеся заряды, мы не интересовались процессами, происходящими в веществе. Свойства среды учитывались формально с помощью магнитной проницаемости m. Для того чтобы разобраться в магнитных свойствах сред и их влиянии на магнитную индукцию, необходимо рассмотреть действие магнитного поля на атомы и молекулы вещества. Опыт показывает, что все вещества, помещенные в магнитное поле, намагничиваются. Рассмотрим причину этого явления с точки зрения строения атомов и молекул, положив в основу гипотезу Ампера, согласно которой в любом теле существуют микроскопические токи, обусловленные движением электронов в атомах и молекулах. Для качественного объяснения магнитных явлений с достаточным приближением можно считать, что электрон движется в атоме по круговым орбитам. Электрон, движущийся по одной из таких орбит, эквивалентен круговому току, поэтому он обладаеторбитальным магнитным моментом pm=ISn, модуль которого
где I=en — сила тока, n — частота вращения электрона по орбите, S — площадь орбиты. Если электрон движется по часовой стрелке, то ток направлен против часовой стрелки и вектор рm (в соответствии с правилом правого винта) направлен перпендикулярно плоскости орбиты электрона, как указано на рисунке. С другой стороны, движущийся по орбите электрон обладает механическим моментом импульса Le, модуль которого, согласно
где v = 2pn, pr2 = S. Вектор Le (его направление также определяется по правилу правого винта) называется орбитальным механическим моментом электрона. Из рисунка следует, что направления рm и Le, противоположны, поэтому, учитывая выражения (1) и (2), получим
где величина
называется гиромагнитным отношением орбитальных моментов (общепринято писать со знаком «–», указывающим на то, что направления моментов противоположны). Это отношение, определяемое универсальными постоянными, одинаково для любой орбиты, хотя для разных орбит значения v и r различны. Формула (4) выведена для круговой орбиты, но она справедлива и для эллиптических орбит. Экспериментальное определение гиромагнитного отношения проведено в опытах Эйнштейна и де Гааза* (5), которые наблюдали поворот свободно подвешенного на тончайшей кварцевой нити железного стержня при его намагничении во внешнем магнитном поле (по обмотке соленоида пропускался переменный ток с частотой, равной частоте крутильных колебаний стержня). При исследовании вынужденных крутильных колебаний стержня определялось гиромагнитное отношение, которое оказалось равным –(e/m). Таким образом, знак носителей, обусловливающих молекулярные токи, совпадал со знаком заряда электрона, а гиромагнитное отношение оказалось в два раза бо2льшим, чем введенная ранее величина g (см. (4)). Для объяснения этого результата, имевшего большое значение для дальнейшего развития физики, было предположено, а впоследствии доказано, что кроме орбитальных моментов (см. (1) и (2)) электрон обладает собственным механическим моментом импульса Les, называемым спином. Считалось, что спин обусловлен вращением электрона вокруг своей оси, что привело к целому ряду противоречий. В настоящее время установлено, что спин является неотъемлемым свойством электрона, подобно его заряду и массе. Спину электрона Les, соответствует собственный (сотовый) магнитный момент рms, пропорциональный Les и направленный в противоположную сторону:
Величина gs называетсягиромагнитным отношением спиновых моментов. Проекция собственного магнитного момента на направление вектора В может принимать только одно из следующих двух значений:
где ħ=h/(2p) (h—постоянная Планка), mb—магнетон Бора, являющийся единицей магнитного момента электрона.
В общем случае магнитный момент электрона складывается из орбитального и спинового магнитных моментов. Магнитный момент атома, следовательно, складывается из магнитных моментов входящих в его состав электронов и магнитного момента ядра (обусловлен магнитными моментами входящих в ядро протонов и нейтронов). Однако магнитные моменты ядер в тысячи раз меньше магнитных моментов электронов, поэтому ими пренебрегают. Таким образом, общий магнитный момент атома (молекулы) pa равен векторной сумме магнитных моментов (орбитальных и спиновых) входящих в атом (молекулу) электронов:
Еще раз обратим внимание на то, что при рассмотрении магнитных моментов электронов и атомов мы пользовались классической теорией, не учитывая ограничений, накладываемых на движение электронов законами квантовой механики. Однако это не противоречит полученным результатам, так как для дальнейшего объяснения намагничивания веществ существенно лишь то, что атомы обладают магнитными моментами. Гиромагни́тноеотноше́ние (магнитомехани́ческоеотноше́ние) — отношение дипольного магнитного моментаэлементарной частицы (или системы элементарных частиц) к её механическому моменту. В системе СИединицей измерения гиромагнитного отношения является с·А·кг−1 = с−1·Тл−1. Часто подразумевается, что гиромагнитное отношение измеряется в единицах q/2mc, где с — скорость света, q и m — заряд и масса частицы, соответственно. В этом случае оно выражается безразмерной величиной. Для различных состояний атомной системы гиромагнитное отношение определяется формулой:
где g — множитель Ланде, γ0 — единица гиромагнитного отношения:
где e — элементарный заряд, me — масса электрона, с — скорость света. В случае ядер, за единицу гиромагнитного отношения принимают величину:
где mp — масса протона. Согласно классической теории, гиромагнитное отношение является коэффициентом пропорциональности между угловой скоростьюпрецессии магнитного момента, помещённого во внешнее магнитное поле, и вектором магнитной индукции.
В квантовой теории гиромагнитным отношением определяется величина расщепления уровней в эффекте Зеемана.
27. Опыты Штерна и Герлаха. Собственный момент импульса (спин) электрона. Спектр собственных значений модуля и z-проекции спина. Спиновое и магнитное спиновое квантовое число. Спектр собственных значений модуля и z-проекции спинового магнитного момента. Гиромагнитное отношение спиновых моментов электрона. Орбитальный магнитный момент.В квантовой теории магнитный момент μ и механический момент М атома следует заменить операторами
Отсюда следует, что изучение свойств магнитного момента электрона сводится к изучению свойств операторов В стационарном состоянии определенные значения могут иметь только модуль магнитного момента
гдеμБ— магнетон Бора: μБ= eћ/2mc. Он играет ролькванта магнитного момента (точнее его проекции μz). Спин — это собственный момент импульса электрона, не связанный с движением в пространстве. Для всех электронов абсолютное значение спина всегда равно s = 1/2. Проекция спина на ось = (магнитное спиновое число ms) может иметь лишь два значения: ms = 1/2 или ms = -1/2 . Электронный слой атома образуют электроны с одинаковой энергией, т. е. с одинаковым n во всех состояниях. ,спиновый магнитный момент и его проекция на произвольную ось Z определяются как
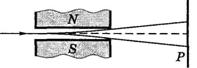
При S = 1/2 ms= +1/2 и -1/2. Опыты Штерна и Герлаха.Наличие у атомов магнитных моментов и их квантование было доказано экспериментально Штерном и Герлахом (1921). В их опытах пучок атомов пропускался сквозь сильно неоднородное поперечное магнитное поле. Необходимая степень неоднородности поля достигалась с помощью специальной формы полюсных наконечников N и S электромагнита. После прохождения магнитного поля пучок атомов попадал на фотопластинку Ри оставлял на ней след.
Если атомы обладают магнитным моментом, то согласно электродинамике на них будет действовать сила, проекция которой на ось Z
где μz — проекция магнитного момента атома на ось Z. Из этой формулы видно, что для получения необходимого эффекта при малых значениях μz нужно обеспечить достаточно большую неоднородность поля, т. е. ∂Bz/∂z. Это и достигалось с помощью указанной формы полюсных наконечников. В отсутствие магнитного поля след пучка на фотопластинке Римел вид одной полоски (z = 0). При включении же магнитного поля наблюдалось расщеплениепучка, что являлось следствием квантованияпроекции магнитного момента μz в формуле (4): μzможет принимать только ряд дискретных значений. В опытах обнаружилось также, что для разных атомов число компонент, на которые расщеплялся пучок, было или нечетным, или четным. Анализ полученных результатов показал, что нечетное число компонент возникает у атомов, обладающих только орбитальным механическим моментом ML, тогда магнитное поле снимает вырождение по L и число компонент (значений mL) будет равно 2L + 1, т. е. нечетным. Если же момент атома является суммой орбитального и спинового, т. е. определяется квантовым числом J, то число компонент будет равно 2J+ 1, и в зависимости от того, полуцелым или целым будет значение J, число компонент будет соответственно четным или нечетным. Установлено, что при помещении атома во внешнее магнитное или электрическое поле спектры атомов становятся еще более мультиплётными. С физической точки зрения это означает, что различные электронные облака находящиеся даже на одном подуровне, по разному реагируют на внешнее магнитное поле. Для обозначения этих подподуровней введено третье,магнитное квантовое число тl, принимающее значения всех целых чисел от -l через 0 до +l. тl= -l,...-2,-1,0,+1.+2,...,+ l То есть: магнитное квантовое число (тl) показывает реакцию орбит на внешнее магнитное или электрическое поле, зависит, от орбитального квантового числа и обозначается целыми числами от -l до +l. Электрон помимо движения "вокруг ядра" вращается и вокруг собственной оси. Для обозначения направления этого вращения введено четвёртое квантовое число – cnuнoвoe (ms).Собственный момент вращения -(спин) имеет два значения, условно обозначенные как +1/2 и -1/2. Таким образом, в настоящее время принимается, что собственный механический момент (спин) и связанный с ним собственный спиновый магнитный моменты являются такими же неотъемлемыми свойствами электрона, как его масса и заряд. Спином обладают не только электроны, но и другие элементарные частицы. Спин элементарных частиц оказывается целым или полуцелым кратным величины
( Таким образом, проекция собственного момента импульса электрона может принимать значения +1/2 Отношение магнитного момента μ частицы к ее механическому моменту L, т.е. к ее моменту импульса, называют гиромагнитным отношением. Для электрона на орбите это отношение равно
28. Описание квантового состояния электрона в атоме водорода. Кратность вырождения энергии электрона в атоме водорода. Полный момент импульса электрона. Спектр собственных значений модуля и z-проекции полного момента импульса. Правила отбора при оптических переходах атома водорода. Решение задачи об энергетических уровнях электрона для атома водорода (а также водородоподобных систем: иона гелия Не+, двукратно ионизованного лития Li++ и др.) сводится к задаче о движении электрона в кулоновском поле ядра. Потенциальная энергия взаимодействия электрона с ядром, обладающим зарядом 2е (для атома водорода Z=1), U(r)=-Ze2/4pe0r, (1) где r — расстояние между электроном и ядром. Графически функция V (r) изображена жирной кривой на рис. 302, неограниченно убывающей (возрастающей по модулю) при уменьшении r, т. е. при приближении электрона к ядру. Состояние электрона в атоме водорода описывается волновой функцией y, удовлетворяющей стационарному уравнению Шредингера, учитывающему значение (1):
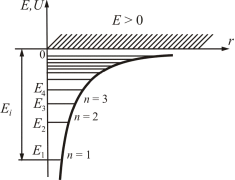
гдет — масса электрона, Е — полная энергия электрона в атоме. Так как поле, в котором движется электрон, является центрально-симметричным, то для решения уравнения (223.2) обычно используют сферическую систему координат: r, q, j. Не вдаваясь в математическое решение этой задачи, ограничимся рассмотрением важнейших результатов, которые из него следуют, пояснив их физический смысл. Энергия.В теории дифференциальных уравнений доказывается, что уравнения типа (2) имеют решения, удовлетворяющие требованиям однозначности, конечности и непрерывности волновой функции y, только при собственных значениях энергии
т. е. для дискретного набора отрицательных значений энергии. Таким образом, как и в случае «потенциальной ямы» с бесконечно высокими «стенками» и гармонического осциллятора, решение уравнения Шредингера для атома водорода приводит к появлению дискретных энергетических уровней. Возможные значения E1, E2, E3 ...показаны на рис. в виде горизонтальных прямых. Самый нижний уровень Е1, отвечающий минимальной возможной энергии,— основной,все остальные (En>E1 n=2, 3, ...) — возбужденные. При E<0 движение электрона является связанным— он находится внутри гиперболической «потенциальной ямы». Из рисунка следует, что по мере роста главного квантового числа n энергетические уровни располагаются теснее и при n=¥ E¥=0. При E>0 движение электрона является свободным;область непрерывного спектра £>0 (заштрихована на рис.) соответствует ионизованному атому.Энергия ионизации атома водорода равна Ei=-E1= те4/ (8h2e20)=13,55 эВ. Выражение (3) совпадает с формулой полученной Бором для энергии атома водорода. Однако если Бору пришлось вводить дополнительные гипотезы (постулаты), то в квантовой механике дискретные значения энергии, являясь следствием самой теории, вытекаютнепосредственно из решения уравнения Шредингера. 2. Квантовые числа.В квантовой механике доказывается, что уравнению Шредингера (2) удовлетворяют собственные функции ynml(r, q, j), определяемыетремя квантовыми числами: главным n, орбитальным l и магнитным ml. Главное квантовое числоn, согласно (223.3), определяет энергетические уровни электронав атоме и может принимать любые целочисленные значения начиная с единицы: n=1,2,3, .... Из решения уравнения Шредингера вытекает, что момент импульса (механический орбитальный момент) электрона квантуется, т. е. не может быть произвольным, а принимает дискретные значения, определяемые формулой Le=hÖ(l(l+1)), (4) где l— орбитальное квантовое число,которое при заданномn принимает значения l=0, 1, ..., (n-1), (5) т. е. всего n значений, и определяет момент импульса электрона ватоме. Из решения уравнений Шредингера следует также, что вектор Leмомента импульса электрона может иметь лишь такие ориентации в пространстве, при которых его проекция Lezна направление z внешнего магнитного поля принимает квантованные значения, кратные h Lеz=hml, (6) где ml— магнитное квантовое число,которое при заданномl может принимать значения ml=0, ±1, ±2, ..., ±l, (7) т. е. всего 2l+1 значений. Таким образом, магнитное квантовое числоml определяет проекцию момента импульса электрона на заданное направление,причем вектор момента импульса электрона в атоме может иметь в пространстве 2l+1 ориентации. Наличие квантового числа ml должно привести в магнитном поле к расщеплению уровня с главным квантовым числом n на 2l+1 подуровней. Соответственно в спектре атома должно наблюдаться расщепление спектральных линий. Действительно, расщепление энергетических уровней в магнитном поле было обнаружено в 1896г. голландским физиком П. Зееманом (1865—1945) и получило название эффекта Зеемана.Расщепление уровней энергии во внешнем электрическом поле, тоже доказанное экспериментально, называется эффектомШтарка. Хотя энергия электрона (3) и зависит только от главного квантового числа n, но каждому собственному значению En(кроме E1) соответствует несколько собственных функций ynlml, отличающихся значениями l и ml. Следовательно, атом водорода может иметь одно и то же значение энергии, находясь в нескольких различных состояниях. Так как при данном n орбитальное квантовое число l может изменяться от 0 до n-1 (см. (223.5)), а каждому значению l соответствует 2l+1 различных значений ml (223.7), то число различных состояний, соответствующих данному n, равно
Квантовые числа и их значения являются следствием решений уравнений Шредингера и условий однозначности, непрерывности и конечности, налагаемых на волновую функцию y. Кроме того, поскольку при движении электрона в атоме существенны волновые свойства электрона, квантовая механика вообще отказывается от классического представления об электронных орбитах. Согласно квантовой механике, каждому энергетическому состоянию соответствует волновая функция, квадрат модуля которой определяет вероятность обнаружения электрона в единице объема. Вероятность обнаружения электрона в различных частях атома различна. Электрон при своем движении как бы «размазан» по всему объему, образуя электронное
облако, плотность (густота) которого характеризует вероятность нахождения электрона в различных точках объема атома. Квантовые числа n и l характеризуют размер и форму электронного облака, а квантовое число ml характеризует ориентацию электронного облака в пространстве. В атомной физике, по аналогии со спектроскопией, состояние электрона, характеризующееся квантовыми числами l=0, называют s-состоянием (электрон в этом состоянии называют s-электроном), l=1 — р-состоянием, l=2 — d-состоянием, l=3 — f-состоянием и т.д. Значение главного квантового числа указывается перед условным обозначением орбитального квантового числа. Например, электроны в состояниях n=2 и l=0 и 1 обозначаются соответственно символами 2s и 2р. На рис. 303 для примера приведено распределение электронной плотности (формы электронного облака) для состояний атома водорода при n=1 и n=2, определяемое │ynlml│2. Как видно из рисунка, оно зависит от n, l и ml. Так, при l=0 электронная плотность отлична от нуля в центре и не зависит от направления (сферически-симметрична), а для остальных состояний в центре равна нулю и зависит от направления. 3. Спектр.Квантовые числа n, l и mlпозволяют более полно описать спектр испускания (поглощения) атома водорода, полученный в теории Бора (см. рис. 294). В квантовой механике вводятся правила отбора,ограничивающие число возможных переходов электронов в атоме, связанных с испусканием и поглощением света. Теоретически доказано и экспериментально подтверждено, что для дипольного излучения электрона, движущегося в центрально-симметричном поле ядра, могут осуществляться только такие переходы, для которых: 1) изменение орбитального квантового числа Dl удовлетворяет условию Dl=±1; (9) 2) изменение магнитного квантового числа Dml удовлетворяет условию Dml=0, ±1. В оптических спектрах указанные правила отбора в основном выполняются. Однако в принципе могут наблюдаться и слабые «запрещенные» линии, например возникающие при переходах с Dl=2. Появление этих линий объясняется тем, что строгая теория, запрещая дипольные переходы, разрешает переходы, соответствующие излучению более сложных систем зарядов, например квадруполей. Вероятность же квадрупольных переходов (переходы с Dl=2) во много раз меньше вероятности дипольных переходов, поэтому «запрещенные» линии и являются слабыми. Учитывая число возможных состояний, соответствующих данномуn, и правило отбора (223.9), рассмотрим спектральные линии атома водорода (рис. 304): серии Лаймана соответствуют переходы np®1s (n=2,3,...); серииБальмера — np®2s, ns®-2p, nd®2p (n=3, 4, ...) и т. д. Переход электрона из основного состояния в возбужденное обусловлен уве
Электрон в атоме может иметь только определенные дискретные (квантованные) значения энергии, которые совпадают с выражением E=-(Z2me4/8ε02h2n2), где n – главное квантовое число. Орбитальный момент импульса L электрона в атоме также может принимать лишь ряд дискретных значений L=(h/2π)√l(l+1), Где l – орбитальное квантовое число. Проекция орбитального момента импульса Lz на выбранное направление OZ (например, направление внешнего магнитного поля) тоже квантуется Lz=(h/2π)m, где m – магнитное квантовое число. Дальнейшие исследования показали, что помимо указанных орбитальных характеристик электрон обладает также собственным моментом импульса Ls. Вырождение энергетических уровней -существование двух или более стационарных состояний квантовой системы (атома, молекулы) с одинаковыми значениями энергии. Система, полная энергия которой определяется заданием оператора Я (гамильтониана), может иметь т стационарных состояний, для которых уравнение Шредингера Hφi = Eφi определяет соответствующие волновые функции φi (i = 1, 2, ..., т) и одно значение энергии Е, одинаковое для всех т состояний. Энергетический уровень с энергиейЕпри m ≠ 1 называется вырожденным, число т различных независимых волновых функций - кратностью вырождения уровня. О состояниях с волновыми функциями φi говорят как о состояниях, вырожденных по энергии, или вырожденных состояниях. Если одному значению энергии отвечает одно состояние, т.е. m=1, уровень наз. невырожденным. Для электрона в атоме полный момент импульса J складывается из орбитального и спинового моментов, и по этому правилу квантовое число полного момента имеет два значения:
В квантовой механике вводятся правила отбора. Они ограничивают число принципиально возможных переходов электронов в атоме, связанных с излучением и поглощением света. Эти правила являются следствием законов сохранения. Закон сохранения момента импульса для процесса испускания атомом одного фотона можно записать так:
где Sф - вектор спина фотона
29. Полный момент импульса многоэлектронного атома. LS-связь. Спектр собственных значений модуля суммарного орбитального момента, спина, модуля и z-проекции полного момента импульса и магнитного момента многоэлектронного атома. Правила отбора при оптических переходах многоэлектронного атома. Каждый электрон в атоме обладает орбитальным моментом импульса M и собственным моментом MS. Механические моменты связанны с соответствующими магнитными моментами, вследствие чего между всеми M и MS имеется взаимодействие. Эти моменты складываются в полный момент атома Mj. Возможны два случая: 1) Моменты M взаимодействуют друг с другом сильнее, чем с моментом MS, которые между собой связанны сильнее, т.о. 2) Каждая пара Рассмотрим нормальную и LS – связь.
Орбитальные квантовые числа li всегда бывают целыми. Соответственно квантовое число L суммарного орбитального момента также бывает целым (либо нулём).
Если число электронов в атоме N является чётным, то квантовое число S принимает все целые значения от N При данных ML и MS квантовое число J результирующего момента MJ может иметь одно из следующих значений: J=L+S,L+S-1,…,|L-S|. Следовательно, J будет целым, если S – целое, и полуцелым, если S – полуцелое. Например: если L=2,S=1; J=3,2,1. Если L=2,S=3/2; J=7/2,5/2,3/2,1/2. Энергия атома зависит от взаимной ориентации магнитных моментов |
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 1781. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||

 .
. при х = 0, должны существовать как прошедшая волна, так и отражённая. Так как ω в этих волнах одна и та же
при х = 0, должны существовать как прошедшая волна, так и отражённая. Так как ω в этих волнах одна и та же  , то в расчётах можно ограничиться только координатной частью этих волн, а именно Ψ( х ).
, то в расчётах можно ограничиться только координатной частью этих волн, а именно Ψ( х ).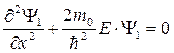

 , где
, где 
 , где
, где 
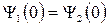 или
или  и
и или
или 
 и
и 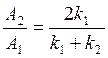



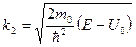 является чисто мнимым. Коэффициент отражения
является чисто мнимым. Коэффициент отражения  т.к. числитель и знаменатель –
т.к. числитель и знаменатель – и зависит от массы т0 , разности ( U0 – E ) и расстояния от границы порога.
и зависит от массы т0 , разности ( U0 – E ) и расстояния от границы порога.












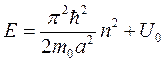 , где n = 1, 2, 3, … ( sin = 0 )
, где n = 1, 2, 3, … ( sin = 0 ) под действием возвращающей квазиупругой силы
под действием возвращающей квазиупругой силы  . Потенциальная энергия такого осциллятора имеет вид
. Потенциальная энергия такого осциллятора имеет вид
 - собственная частота классического гармонического осциллятора. Таким образом, квантово-механическая задача о гармоническом осцилляторе сводится к задаче о движении частицы в параболической потенциальной яме.
- собственная частота классического гармонического осциллятора. Таким образом, квантово-механическая задача о гармоническом осцилляторе сводится к задаче о движении частицы в параболической потенциальной яме.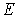 совершает колебания в силовом поле. Точки
совершает колебания в силовом поле. Точки  и
и  , в которых полная энергия частицы равна потенциальной энергии
, в которых полная энергия частицы равна потенциальной энергии  , являются для частицы точками поворота. Частица совершает колебательные движения между стенками потенциальной ямы внутри отрезка
, являются для частицы точками поворота. Частица совершает колебательные движения между стенками потенциальной ямы внутри отрезка  , выйти за пределы которого она не может. Амплитуда колебаний
, выйти за пределы которого она не может. Амплитуда колебаний  определяется выражением
определяется выражением  .
.


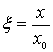 , приводим уравнение к виду
, приводим уравнение к виду
 , а лишь при
, а лишь при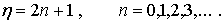
 через
через 
 друг от друга (рис.4.25) .
друг от друга (рис.4.25) .
 , соответствующих значению квантового числа
, соответствующих значению квантового числа 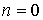 . Отличие от нуля минимальной энергии осциллятора характерно, как мы уже видели, для всех квантовых систем и является следствием соотношения неопределенностей. В реальных квантовых системах, например, кристаллах, эти колебания сохраняются, как показывает опыт, даже при температурах, близких к абсолютному нулю, когда, казалось бы, все тепловое движение должно прекратиться.
. Отличие от нуля минимальной энергии осциллятора характерно, как мы уже видели, для всех квантовых систем и является следствием соотношения неопределенностей. В реальных квантовых системах, например, кристаллах, эти колебания сохраняются, как показывает опыт, даже при температурах, близких к абсолютному нулю, когда, казалось бы, все тепловое движение должно прекратиться. и зависит только от r – расстояния между электроном и протоном, поэтому задачу с таким видом потенциальной энергии обычно решают в сферической системе координат. В общем случае волновая функция является функцией от всех координат и уравнение Шредингера будет иметь вид:
и зависит только от r – расстояния между электроном и протоном, поэтому задачу с таким видом потенциальной энергии обычно решают в сферической системе координат. В общем случае волновая функция является функцией от всех координат и уравнение Шредингера будет иметь вид: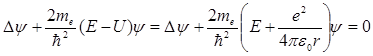 .
.
 Подставив в выражение оператора Лапласа в сферических координатах, получим уравнение Шредингера в следующем виде:
Подставив в выражение оператора Лапласа в сферических координатах, получим уравнение Шредингера в следующем виде: .
. ,
, . Выражение для значений энергий En(21.23) полностью совпадает с результатами теории Бора (19.15). Для атома водорода значение n = 1 соответствует основному состоянию электрона, значение n = ∞ – свободному электрону (E∞ = 0). Отрицательные значения энергии соответствуют связанному состоянию электрона, когда он находится внутри потенциальной ямы и имеет большие отрицательные значения потенциальной энергии (21.20). Положительными значениями энергии электрон обладает в свободном состоянии, когда он покидает пределы атома, и его энергетический спектр становится непрерывным, т.е. область E > 0 соответствует ионизированному атому.
. Выражение для значений энергий En(21.23) полностью совпадает с результатами теории Бора (19.15). Для атома водорода значение n = 1 соответствует основному состоянию электрона, значение n = ∞ – свободному электрону (E∞ = 0). Отрицательные значения энергии соответствуют связанному состоянию электрона, когда он находится внутри потенциальной ямы и имеет большие отрицательные значения потенциальной энергии (21.20). Положительными значениями энергии электрон обладает в свободном состоянии, когда он покидает пределы атома, и его энергетический спектр становится непрерывным, т.е. область E > 0 соответствует ионизированному атому.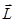 относительно начала координатО (центр орбиты электрона на рис. 21.7) в классической механике определяется векторным произведением
относительно начала координатО (центр орбиты электрона на рис. 21.7) в классической механике определяется векторным произведением  , где вектора
, где вектора  и
и  являются соответственно радиус-вектором частицы и ее импульсом.
являются соответственно радиус-вектором частицы и ее импульсом.
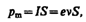 (1)
(1) (2)
(2) (3)
(3) (4)
(4) (5)
(5)
 (.6)
(.6)



 и
и  :
: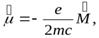

 . А так как операторы
. А так как операторы  отличаются друг от друга только постоянным множителем, то их свойства совершенно аналогичны: магнитный и механический моменты квантуются по одинаковым правилам.
отличаются друг от друга только постоянным множителем, то их свойства совершенно аналогичны: магнитный и механический моменты квантуются по одинаковым правилам. и одна из его проекций на произвольнуюосьZ. Имея в виду (1), а запишем собственные значения операторов
и одна из его проекций на произвольнуюосьZ. Имея в виду (1), а запишем собственные значения операторов  L = 0, 1, 2, ...
L = 0, 1, 2, ...
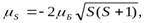



 , которая равна постоянной Планка
, которая равна постоянной Планка  , деленной на
, деленной на  .
. (8) В частности, для электрона собственный
(8) В частности, для электрона собственный  , в связи с чем говорят, что спин электрона равен ½. Таким образом,
, в связи с чем говорят, что спин электрона равен ½. Таким образом,  )
)

 (2)
(2) (3)
(3) (8)
(8)
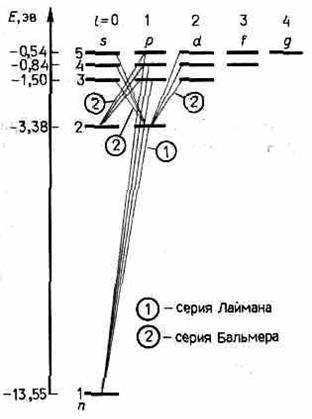 личением энергии атома и может происходить только при сообщении атому энергии извне, например за счет поглощения атомом фотона. Так как поглощающий атом находится обычно в основном состоянии, то спектр атома водорода должен состоять из линий, соответствующих переходам 1s ®np (n=2, 3, ...), что находится в полном согласии с опытом.
личением энергии атома и может происходить только при сообщении атому энергии извне, например за счет поглощения атомом фотона. Так как поглощающий атом находится обычно в основном состоянии, то спектр атома водорода должен состоять из линий, соответствующих переходам 1s ®np (n=2, 3, ...), что находится в полном согласии с опытом.
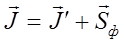 ,
, и
и  - моменты импульса атома до и после излучения соответственно (в единицах
- моменты импульса атома до и после излучения соответственно (в единицах  ),
), ;
;  ;
; 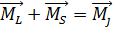 - нормальная связь.
- нормальная связь. и
и  взаимодействуют между собой сильнее, чем с подобными моментами других электронов, т.о.
взаимодействуют между собой сильнее, чем с подобными моментами других электронов, т.о.  --->
--->  - называется jj – связью и наблюдается у тяжёлых атомов.
- называется jj – связью и наблюдается у тяжёлых атомов.
 …;
…;  +…;
+…;  .
. =L(L+1);
=L(L+1);  =S(S+1)
=S(S+1) (все
(все  ), до нуля, когда (
), до нуля, когда (  ). При нечётном N квантовое число S принимает все полуцелые значения от N
). При нечётном N квантовое число S принимает все полуцелые значения от N