Распределение Бозе-Эйнштейна

Обозначим через W, число различных способов, которыми можно разместить N, частиц в r_i ячеек. Так как частицы в квантовом случае считаются неразличимыми, то эти способы могут отличаться друг от друга только числом частиц в ячейках, при фиксированном числе частиц в ящике N_i. Разные способы отличаются друг из друга путем переноса частиц из ячейки в ячейку (обменом местами частиц и перегородок).

Зафиксировав каждое такое распределение, оценим всевозможные несущественные (т.е. не дающие новых способов распределения) перестановки частиц друг с другом (их число равно N_i!) и перегородок друг с другом (их число при r, ячеек равно (r_i-1)!)

Очевидно, что все число перестановок из всех этих (N_i +г_i-1) объектов, включающих и частицы и перегородки.

Распределение Ферми - Дирака

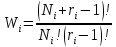
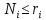Если учесть принцип запрета Паули, то в каждой ячейке одного ящика не может быть больше одной частицы, т.е. . Поскольку при этом частицы неразличимы, то различные способы их размещения по ячейкам в ящике различаются только тем, какие ячейки заняты одной частицей, а какие свободны, или иначе говоря, перестановками пустых ячеек 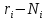и занятых , ячеек между собой т.е. перестановкой всех 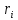, ячеек: