
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Волновое уравнение для свободно движущейся частицы и его обобщение Шрёдингером. Нестационарное уравнение Шрёдингера.Для того чтобы описать распределение вероятности нахождения частицы в данный момент времени в некоторой точке пространства, введем функцию, которая является функцией времени и координат, обозначается греческой буквой ψ и называется волновой функцией или просто пси-функцией. Свободная частица – частица, движущаяся в отсутствие внешних полей. Т.к. на свободную частицу (пусть она движется вдоль оси x) силы не действуют, то потенциальная энергия частицы и ее можно принять равной нулю. Тогда полная энергия частицы совпадает с ее кинетической энергией. В таком случае уравнение Шредингера для стационарных состояний примет вид:
Прямой подстановкой можно убедиться в том, что частным решением уравнения (1) является функция
Функция
где Функция (3) представляет собой плоскую монохроматическую волну де Бройля. Нестационарное уравнение Шредингера имеет вид
здесь m – масса частицы, i – мнимая единица,
U(x,y,z,t) – в рамках наших задач потенциальная энергия частицы, движущейся в силовом поле. Из уравнения Шредингера следует, что вид пси-функции определяется функцией U, т.е. в конечном счете, характером сил, действующих на частицу. Уравнение Шредингера дополняется важными условиями, которые накладываются на пси-функцию. Этих условий три: 1) функция ψ должна быть конечной, непрерывной и однозначной;  2) производные 3) функция
Волновая функция и ее свойства. Принцип суперпозиции состояний. Скалярное произведение пси-функций. Нормированная пси-функция и ее содержательный смысл. Плотность вероятности. Условие нормировки. Волнова́яфу́нкция, или пси-фу́нкция
где |x= |x1, x2, …, xn— координатныйбазисныйвектор, а Согласно копенгагенской интерпретации квантовой механики плотность вероятности нахождения частицы в данной точке конфигурационного пространства в данный момент времени считается равной квадратуабсолютного значения волновой функции этого состояния в координатном представлении. Свойства: 2) волновая функция должна быть однозначной (вероятность не может быть неоднозначной величиной). 3) волновая функция должна быть непрерывной (вероятность не может изменяться скачком). 4) функция может интерферировать сама с собой 5) абсолютное значение функции велико там, где наиболее вероятно нахождение частицы или фотона 6) функция описывает поведение отдельной частицы или фотона, а не статистическое распределение многих частиц. Волновая функция удовлетворяет принципу суперпозиции: если система может находиться в различных состояниях, описываемых волновыми функциями
где Cn (n = 1, 2, ...) – комплексные числа. Еслиобеволновыефункции, начальнуюψиконечнуюφ, отнормироватьнаединицу, тоскалярноепроизведениедаетамплитудувероятноститого, чтосистема, находившаясявсостоянииψ, будетобнаруженавсостоянииϕ. Другимисловами, мыимеемсистемувсостоянииψиставимопыт,которыйдолженответитьнавопрос: ≪А ненаходитсялисистемавсостоянииϕ?≫Причемеслиответбудетположительным, тосистемаивсамомделеокажетсявэтом состоянии. Скалярное произведение
задает соответствующую амплитуду вероятности. Волновая функция
Это условие выражает тот факт, что вероятность обнаружить частицу с данной волновой функцией где-либо в пространстве равна единице. В общем случае интегрирование должно производиться по всем переменным, от которых зависит волновая функция в данном представлении. Условие нормировки для вероятности состояния физической системы отражает факт: если физическая система существует, то она находится в одном из доступных ей состояний. Если состояние системы характеризуется случайной величиной
Утверждается, что для достаточно малого интервала изменений
Знание плотности вероятности позволяет найти вероятность для любой области, в которой определена плотность. Условие нормировки для плотности вероятности записывается следующим образом
Важными числовыми характеристиками случайной величины xявляются ее среднее значение
Оператор в пространстве состояний микрочастицы. Сложение и умножение на множестве операторов. Коммутатор операторов. Линейный оператор. Оператор, сопряженный данному оператору. Самосопряженный оператор. Эрмитов оператор. Определение 1.Оператором Определение 2.Оператором
Определение 3. Суммой операторов Определение 4.Произведением операторов Операторы, вообще говоря, образуют алгебру некоммутирующих величин Определение 5.Оператор
Определение 6.Если в результате действия оператора Определение 7.Совокупность всех собственных значений Определение 8.Если каждому собственному значению Определение 9.Оператора
Все физические операторы, введенные ранее Теорема 1.Собственные значения эрмитовых операторов всегда явл. действительными числами. Определение 10.Функция Теорема 2.Собственные функции линейных эрмитовых операторов взаимно ортогональны.
Оператор
. Собственные значения и собственные функции оператора. Спектр собственных значений оператора. Кратность вырождения. Физический смысл спектра собственных значений эрмитова оператора, поставленного в соответствие динамической переменной. Среднее значение динамической переменной. Собственные значения оператора, сопоставляемого данной механической величине, суть те значения, которые может принять эта величина в условиях, создаваемых ее измерением. Основные свойства собственных функций. Значения, которые может принимать данная физическая величина Если при действии оператора на некоторую функцию получается та же самая функция, умноженная на число, то есть если
то такую функцию называют собственной функцией оператора Квантовомеханические операторы имеют не одну, а множество собственных функций и соответствующих им собственных значений. При этом совокупность собственных значений называют спектром оператора. Спектр оператора
Спектр собственных значений оператора может быть и непрерывным, когда в (3.43) оказываются возможными все значения В ряде случаев одному собственному значению Собственные функции эрмитового оператора с дискретным спектром образуют полную систему функций, т.е. обладают свойством полноты. Это верно для функций квантовой механики. Это означает, что произвольную функцию можно разложить по собственным функциям эрмитового оператора как по базису. Физический смысл спектра собственных значений эрмитова оператора, поставленного в соответствие динамической переменной, устанавливается следующим утверждением: спектр собственных значений эрмитова оператора, поставленного в соответствие динамической переменной, исчерпывает все возможные результаты ее измерения. Пусть мы имеет какую-то переменную A, и этой переменной соответствует оператор
Среднее значение динамической величины, полученное в результате многих измерений, равно математическому ожиданию этой величины, вычисленному с помощью её динамического оператора. |
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 730. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (1)
(1) , гдеA=const и k=const, с собственным значением энергии:
, гдеA=const и k=const, с собственным значением энергии: (2)
(2) представляет собой только координатную часть волновой функции
представляет собой только координатную часть волновой функции  . Зависящую от времени волновую функцию можно представить в виде:
. Зависящую от времени волновую функцию можно представить в виде: (3)
(3) .
. ,
, - оператор Лапласа, результат действия которого на некоторую функцию
- оператор Лапласа, результат действия которого на некоторую функцию .
. должны быть непрерывны
должны быть непрерывны должна быть интегрируема, т.е. интеграл
должна быть интегрируема, т.е. интеграл 
 — комплекснозначная функция, используемая в квантовой механике для описания чистого состояния системы. Является коэффициентом разложения вектора состояния по базису (обычно координатному):
— комплекснозначная функция, используемая в квантовой механике для описания чистого состояния системы. Является коэффициентом разложения вектора состояния по базису (обычно координатному):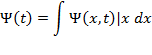
 — волноваяфункциявкоординатномпредставлении.
— волноваяфункциявкоординатномпредставлении. 1,
1, 
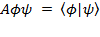

 , принимающей любые значения от
, принимающей любые значения от  до
до  , то определение вероятности лишено смысла, поскольку множество значений
, то определение вероятности лишено смысла, поскольку множество значений 
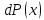 пропорциональна величине достаточно много интервала измерений переменной
пропорциональна величине достаточно много интервала измерений переменной  , а коэффициент пропорциональности
, а коэффициент пропорциональности  не зависит от величины этого интервала и называется плотностью вероятности
не зависит от величины этого интервала и называется плотностью вероятности

 и дисперсия
и дисперсия  .
. назыв. правило, по которому одной функции
назыв. правило, по которому одной функции  ставится в соответствии другая функция
ставится в соответствии другая функция 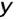 тех же независимых переменных
тех же независимых переменных 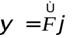 .
.
 назыв. оператор
назыв. оператор  , который если для произвольной функции
, который если для произвольной функции  .
. , удовл. условию:
, удовл. условию:  .
. .
. назыв. коммутатором операторов
назыв. коммутатором операторов 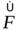 и
и  .
.



 .
.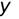 ,в результате получается та же функция, умноженная на постоянную
,в результате получается та же функция, умноженная на постоянную  , т.е.
, т.е.  , где
, где  различных собственных функций
различных собственных функций  , то спектр назыв. вырожденным с кратностью вырождения
, то спектр назыв. вырожденным с кратностью вырождения  и
и  .
. явл. линейными и эрмитовыми.
явл. линейными и эрмитовыми. .
. называется сопряженным оператору
называется сопряженным оператору 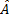 , если для любых
, если для любых  и
и  справедливо равенство
справедливо равенство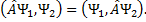
 называют в квантовой механике ее собственными значениями. Нахождение таких значений тесно связано с математической задачей определения собственных функций и соответствующих им собственных значений оператора
называют в квантовой механике ее собственными значениями. Нахождение таких значений тесно связано с математической задачей определения собственных функций и соответствующих им собственных значений оператора  .
.
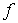 его собственным значением.
его собственным значением. для
для  соответствующих набору собственных функций
соответствующих набору собственных функций  , которые представляют собой регулярные решения уравнения вида
, которые представляют собой регулярные решения уравнения вида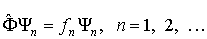
 , либо состоящим из отдельных полос, таких что возможные значения
, либо состоящим из отдельных полос, таких что возможные значения  лежат в ряде интервалов.
лежат в ряде интервалов. оператора
оператора  . Такие случаи называются вырожденными, а число
. Такие случаи называются вырожденными, а число  таких функций называется кратностью вырождения.
таких функций называется кратностью вырождения. , тогда среднее значение переменнойAв состоянии
, тогда среднее значение переменнойAв состоянии  (угловыми скобками будем обозначать) будет определяться так:
(угловыми скобками будем обозначать) будет определяться так: