
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Операція здобуття кореня n-ого степеня з комплексного числа⇐ ПредыдущаяСтр 22 из 22 Нехай задане комплексне число Означення Коренем n-ого (n≥2) степеня з комплексного числа
Нехай число
Тобто, Порівнюючи дійсні та уявні частини, отримаємо дійсну нелінійну систему рівнянь.
Більш складна система виникає, якщо таким шляхом вилучати корені степеня n≥3. Розглянемо це питання для комплексного числа Шукатимемо За означенням, користуючись формулою Муавра, маємо
З цієї рівності випливає
Звідси випливає Отже
Насправді, щоб отримати всі корені достатньо змінювати
Тоді
Скористаємося періодичністю тригонометричних функцій, тоді
Отже, отримали формули
Зауваження В шкільному курсі символ Корені n-ого степеня з одниці Застосуємо отриману формулу в окремому випадку при
Тоді,
Корені Властивість 1 Добуток двох коренів n-ого степеня з одиниці є також коренем n-ого степеня з одиниці. Доведення. Нехай Розглянемо 
Внаслідок асоціативності і комутативності множення комплексних чисел маємо
що і треба було довести. З цієї властивості випливає наслідок. Наслідок 1. Будь-який натуральний степінь кореня n-ого степеня з одиниці є також коренем n-ого степеня з одиниці. Властивість 2 Число обернене до кореня n-ого степеня з одиниці є також коренем n-ого степеня з одиниці. Доведення. Нехай Розглянемо Наслідок 2. Будь-який від`ємний степінь кореня n-ого степеня з одиниці є також коренем n-ого степеня з одиниці. Це випливає з того, що Оскільки В подальшому ці властивості в розділі теорії груп дозволять побудувати мультиплікативну групу коренів n-ого степеня з одиниці. Розглянемо властивість, важливу з практичної точки зору. Властивість 3. Добуток кореня n-ого степеня з числа Доведення. Нехай Розглянемо З цієї властивості випливає, що всі корені n-ого степеня з числа Комплексно-спряжені числа Означення. Числа вигляду Очевидно, що сума і добуток комплексно-спряжених чисел
є дійними числами. Відмітимо важливі для подальшого властивості. Властивість 1. Число комплексно-спряжене до суми дорівнює сумі чисел спряжених до доданків.
Доведення. Нехай Аналогічно можна довести (пропонується зробити це самостійно): 1. 2. 3. Нерівність трикутника Як і для дійсних чисел для комплексних чисел має місце нерівність трикутника
Доведення. Спочатку доведемо геометрично, що Зобразимо на площині комплексні числа
Тоді, за нерівністю трикутника маємо
Отже, друга частина нерівності доведена.
Доведення першої частини нерівності зведемо до другої частини. Для цього запишемо очевидну нерівность.
Застосуємо до цієї суми доведену нерівність
Зауважимо, що
А тому,
що і треба було довести. Якщо в нерівності трикутника покласти Література
1. Ильин В.А. Аналитическая геометрия/В.А.Ильин, Э.Г.Позняк. – М.:Наука, 1971. – 232с. 2. Ильин В.А. Линейная алгебра/В.А.Ильин, Э.Г.Позняк. – М.:Наука, 1984. – 232с. 3. Завало С.Т. Курс алгебри. – К.: Вища шк., 1985. – 504с. 4. Александров П.С. Курс аналитической геометрии и линейной алгебры. – М.:Наука, 1979. – 512с. 5. Курош А.Г. Курс высшей алгебры. – М.:Наука, 1975. – 431с. 6. Моденов П.С. Аналитическая геометрия. – М.: Изд-во МГУ, 1969. – 670с. 7. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. – М.: Наука, 1984. – 320с. 8. Цубербиллер О.Н. Задачи и упражнения по аналитической геометрии. – М.: Гостехиздат, 1949. – 336с. 9. Тышкевич Р.И. Линейная алгебра и аналитическая геометрия/ Р.И.Тышкевич, А.С. Феденко. – Минск: Вышейшая школа, 1968. – 505с. 10. Проскуряков И.В. Сборник задач по линейной алгебре. – М.: Наука, 1984. – 336с. 11. Бурдун А.А. Сборник задач по алгебре и аналитической геометрии/ А.А.Бурдун, Е.А.Мурашко, М.М.Толкачев, А.С.Феденко. – Мн.: Універсітэцкае, 1999. – 302с. 12. Гетманцев В.Д. Лінійна алгебра і лінійне програмування. – К: Либідь, 2001. – 256с. 13. Гриньов Б.В. Аналітична геометрія./Б.В.Гриньов, І.К.Кириченко. – Харків: Гімназія, 2008. – 344с. 14. Гриньов Б.В. Вища алгебра./Б.В.Гриньов, І.К.Кириченко. – Харків: Гімназія, 2008. – 184с. 15. Гриньов Б.В. Векторна алгебра./Б.В.Гриньов, І.К.Кириченко. – Харків: Гімназія, 2008. – 164с. 16. Варех Н.В. Лабораторні роботи до курсу лінійної алгебри та геометрії/ Н.В.Варех, М.П.Д’яченко, Н.А.Лихолат, С.Д.Сотникова. – Д.: РВВ ДДУ, 1992. – 52с. 17. Варех Н.В. Методи обчислення визначників n-го порядку/Н.В.Варех, М.П.Д’яченко, В.Б.Круглушина. – Д.: РВВ ДДУ, 1995. – 28с. 18. Варех Н.В. Лінійні оператори/Н.В.Варех, М.П.Д’яченко. – Д.: РВВ ДДУ, 2003. – 28с. 19. Варех Н.В. Методические указания к самостоятельному изучению раздела «Многочлены от одной переменной»/ Н.В.Варех, Н.А.Лихолат, О.М.Ревин, В.Н.Трофимов. – Д.: РВВ ДДУ, 1989. – 32с. 20. Варех Н.В. Методические указания к самостоятельному изучению раздела «Плоскость»/ Н.В.Варех, Н.А.Лихолат, О.М.Ревин, В.Н.Трофимов. – Д.: РВВ ДДУ,. – 1992. – 32с. 21. Варех Н.В. Практикум із дисципліни «Алгебра та геометрія»/Н.В.Варех, М.П.Д’яченко. – Д.: РВВ ДНУ, 2005. – 48с. 22. Варех Н.В. Практикум із дисципліни «Алгебра та геометрія»/Н.В.Варех, М.П.Д’яченко. – Д.: РВВ ДНУ, 2007. – 76с. 23. Варех Н.В. Практикум із векторної алгебри/Н.В.Варех, Н.Л.Козакова. – Д.: РВВ ДНУ, 2007. – 52с. |
|||||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 314. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
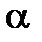 .
. таке, що
таке, що .
.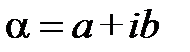 . Шукатимемо
. Шукатимемо  . Розглянемо найпростіший випадок n=1. Тоді за попереднім означенням треба знайти дійсні числа с і d такі що
. Розглянемо найпростіший випадок n=1. Тоді за попереднім означенням треба знайти дійсні числа с і d такі що
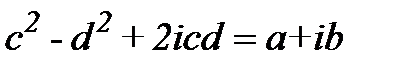

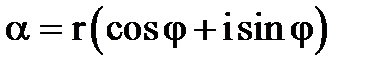 .
.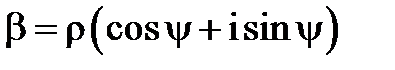 .
. .
.
 (арифметичний корінь),
(арифметичний корінь),  .
.
 . Нехай
. Нехай  . Доведемо, що
. Доведемо, що  збігатиметься з одним з коренів
збігатиметься з одним з коренів  . Поділимо к на n:
. Поділимо к на n: .
.

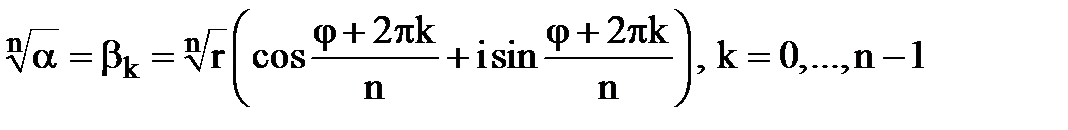
 вживався лише для арифметичних коренів. Тепер ми вживатимемо цей символ в більш широкому сенсі.
вживався лише для арифметичних коренів. Тепер ми вживатимемо цей символ в більш широкому сенсі. . Подамо
. Подамо  в тригонометричній формі:
в тригонометричній формі:
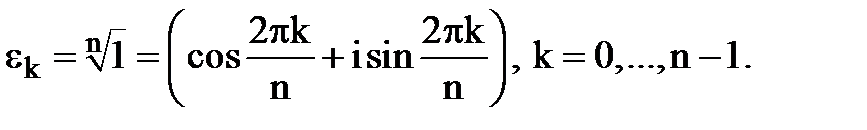
 n-ого степеня з 1 мають цікаві властивості.
n-ого степеня з 1 мають цікаві властивості. та
та  - корені n-ого степеня з одиниці, тобто
- корені n-ого степеня з одиниці, тобто  . Треба довести, що
. Треба довести, що 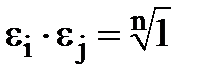 , тобто що
, тобто що  .
.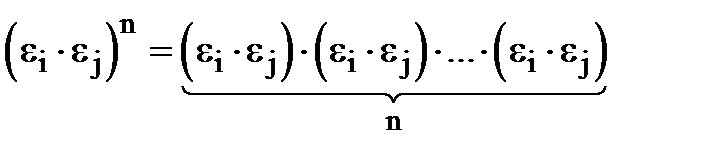

 ,
,  - число обернене до
- число обернене до  , тому
, тому  . Треба довести, що
. Треба довести, що 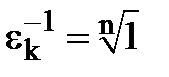 , тобто
, тобто 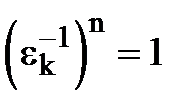 .
. . Звідси внаслідок коммутативності і ассоциативності множення маємо
. Звідси внаслідок коммутативності і ассоциативності множення маємо  . Оскільки
. Оскільки  , то
, то  .
.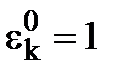 , то з наслідків 1 та 2 випливає: будь-який цілий степінь кореня n-ого степеня з одиниці також є коренем n-ого степеня з одиниці.
, то з наслідків 1 та 2 випливає: будь-який цілий степінь кореня n-ого степеня з одиниці також є коренем n-ого степеня з одиниці.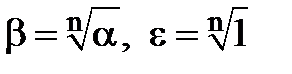 . Треба довести, що
. Треба довести, що  , тобто що
, тобто що 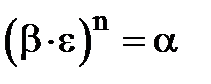 .
.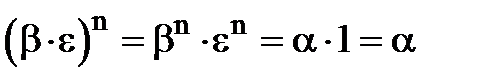 , що і треба було довести.
, що і треба було довести. називаються комплексно-спряженими.
називаються комплексно-спряженими. ,
,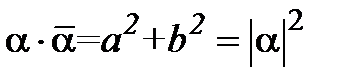 .
. .
. , тоді
, тоді  . Тому
. Тому  .
. ;
; ;
;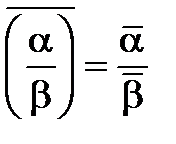 .
.
 .
. , побудуємо геометрично суму
, побудуємо геометрично суму  . Отримаємо трикутник
. Отримаємо трикутник  зі сторонами
зі сторонами
 ,
, .
. (довести самостійно). Тоді маємо нерівність в області дійсних чисел
(довести самостійно). Тоді маємо нерівність в області дійсних чисел .
. ,
, , то отримаємо і таку нерівність
, то отримаємо і таку нерівність  .
.