
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Тригонометрична форма комплексного числа. Операції множення та ділення в тригонометричній формі.Нехай задано комплексне число a = (a, b) = a + b×і , де a і b – декартові прямокутні координати точки a, що зображає комплексне число. Введемо полярну систему координат таким чином, щоб полюс її збігався з початком декартової системи, а полярна вісь – з вісью 0х. Нехай точка a має полярні координати a (r,j). Використовуючи зв¢язок між декартовою і полярною системами, маємо a = a + bi = r×cosj + r×i×sinj Звідси a = r (cosj + i×sinj), отримана форма запису комплесного числа називається тригонометричною формою, r – модуль комплексного числа a ( r = ½a½), j - аргумент к a (j = arg a). Таким чином ми довели, що будь-яке комплексне число можна записати в тригонометричній формі.
Розглянемо операції множення та ділення в тригонометричній формі. Нехай задно два комплексних числа в тригонометрчній формі a = r1 (cos b = r2 (cos Треба одержати a× b = r (cos j + i sin j) . Для того, щоб це зробити перейдемо від тригонометричної фори до агебраїчної і перемножимо. a× b = ( = тобто a×b = Звідси випливає: r=r1r2, r=|a× b|, r1=|a|, r2=|b|, |a× b|=|a|×|b|. j = Таким чином ми одержали, що 1) модуль добутку двох комплексних чисел дорівнює добутку модулів. 2) аргумент добутку двох чисел дорівнює сумі аргументів. Підсумовуючи це, маємо Правило: Для того, щоб перемножити два числа в тригонометричній формі, треба перемножити їх модулі і додати аргументи. Розглянемо частку двох комплексних чисел в тригонометричній формі
Домножимо чисельник і знаменник на
Отже, отримали правило

Операції піднесення до степеня Поняття цілого степеня комплексного числа Домовились вважати 1) 2) Для корректності введеного поняття треба виконати вправу: 1) Довести
2) Довести 1. Розглянемо спочатку операцію піднесення в алгебраїчній формі. Нехай задано число
Розглянемо таблицю множення числа і
Використовуючи таблицю множення та виділяючи дійсну та уявну частину, отримаємо
2. Розглянемо операцію піднесення до степеню, коли
Використовуючи правило множення комплексних чисел в тригонометричній формі, маємо
Застосуємо отримані рівності (1) і (2) для знаходження розкладання Застосуємо до числа
Застосуємо формулу (1) при
Порівнюючи в формулах (3) і (4) дійсні та уявні частини, отримаємо
|
||||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 402. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
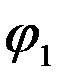 + i sin
+ i sin 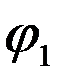 )
)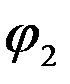 + i sin
+ i sin  ) .
) .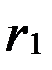 cos
cos 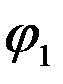 +
+  sin
sin 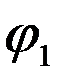 ) (
) ( 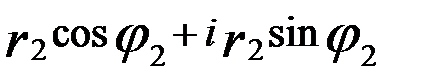 ) =
) =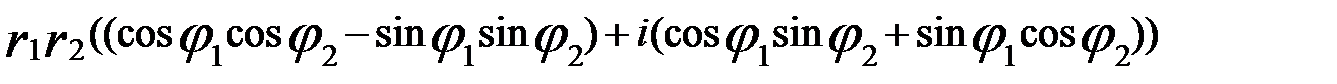 ,
,
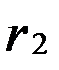 (cos(
(cos( 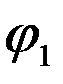 +
+ 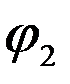 )+i×sin(
)+i×sin( 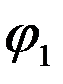 +
+ 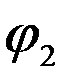 ) ).
) ).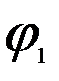 +
+ 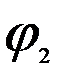 , j = arg (ab) ,
, j = arg (ab) , 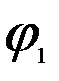 = arg a ,
= arg a , 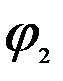 = arg b , arg (ab) = arg a + arg b .
= arg b , arg (ab) = arg a + arg b .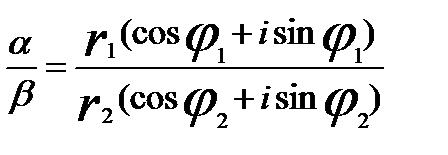

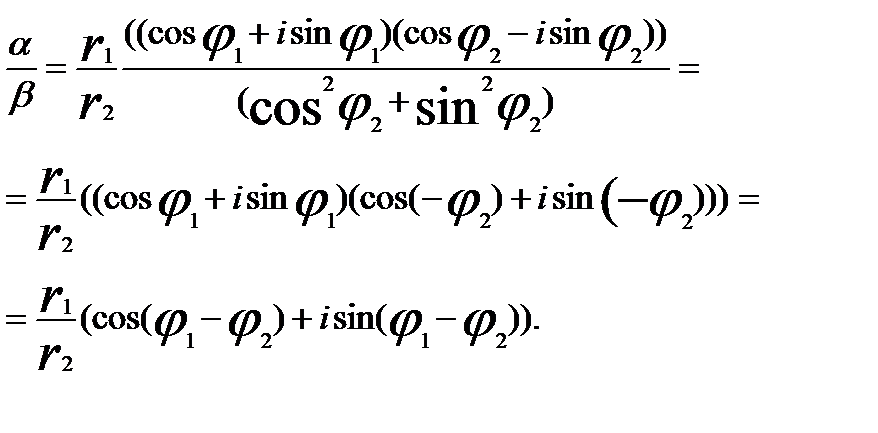
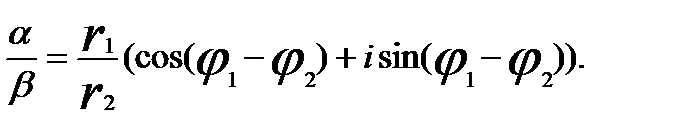
 , arg (
, arg (  ) =
) = 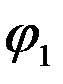 ×
× 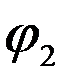 = arg a - arg b.
= arg a - arg b.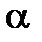 вводиться так само як і для дійсного числа. Нагадаємо, що
вводиться так само як і для дійсного числа. Нагадаємо, що 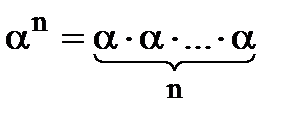 при
при  .
. . Для введення
. Для введення 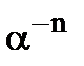 існують два шляхи.
існують два шляхи.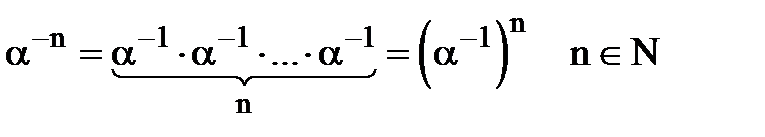 , де
, де 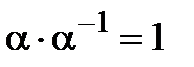
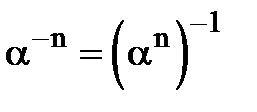

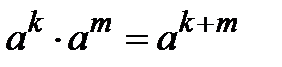 при
при  .
.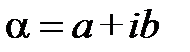 . Оскільки з попередніх означень випливає, що піднесення до цілого степеня зводиться до піднесення до натурального степеня, то можна скористатися формулою Бінома Ньютона:
. Оскільки з попередніх означень випливає, що піднесення до цілого степеня зводиться до піднесення до натурального степеня, то можна скористатися формулою Бінома Ньютона:
 з цього випливає
з цього випливає 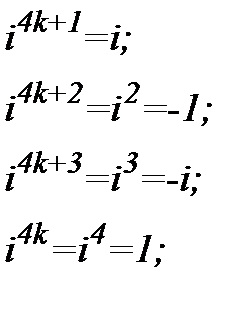
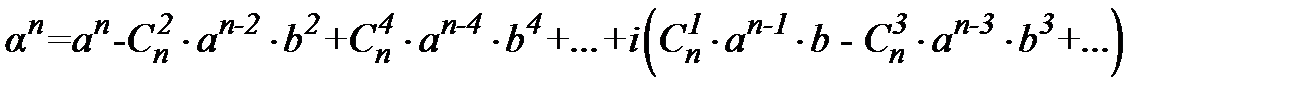
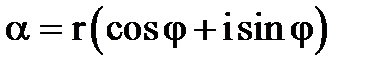
 .
.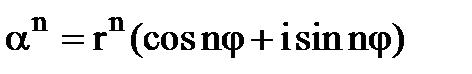 - формула Муавра
- формула Муавра
 і
і  через
через 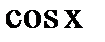 і
і  . Окремі випадки цих формул при n=2,3 відомі зі шкільного курсу.
. Окремі випадки цих формул при n=2,3 відомі зі шкільного курсу.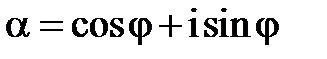 формулу (2). В тригонометричній формі
формулу (2). В тригонометричній формі 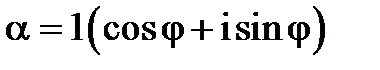
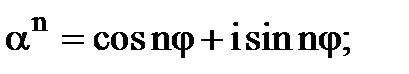 (3)
(3) , отримаємо
, отримаємо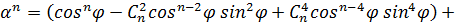


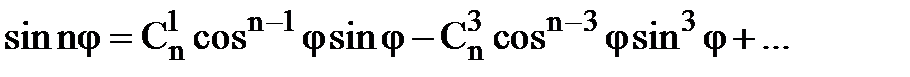 (4)
(4)