
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Потенциальное силовое поле и силовая функцияРабота на перемещение
Вычислить данный интеграл, не зная происходящего движения Силовым полем называется часть пространства, в каждой точке которого на помещённую материальную частицу действует определённая по модулю и направлению сила, зависящая от положения частицы. Примером силового поля служит поле тяготения планеты или Солнца. Силы, определяющие проекции на оси координат, задаются уравнениями:
Однако, если окажется, что выражение, стоящее в формуле (4.33) под знаком интеграла и представляющее собой элементарную работу силы, будет полным дифференциалом некоторой функции
Функция
где Следовательно, работа поступательной силы равна разности значений силовой функции в конечной и начальной точках пути, и не зависит от вида траектории движущейся точки . Силы, работа которых зависит от вида траектории или закона движения точки приложенной силы, называются непотенциальными (силы трения и сопротивления среды).  К потенциальным относятся силы тяжести, упругости тяготения. Для силы тяжести, если ось z направлена вверх:
для упругой силы, действующей вдоль оси Ox:
для силы тяготения:
Потенциальная энергия Для потенциальных сил можно вывести понятие о потенциальной энергии как о величине, «характеризующей запас работы», которым обладает материальная точка в данном пункте силового поля. Потенциальной энергией материальной точки в данном положении М называется скалярная величина П, равная той же работе, которую
Будем считать нулевые значения точек для функции
где U – значение силовой функции в точке М поля. Отсюда
т. е. потенциальная энергия в любой точке равна значению силовой функции в этой точке, взятому с обратным знаком. Отсюда видно, что вместо силовой функции можно пользоваться понятием потенциальной энергии. В частности, работу потенциальной силы (4.34) можно вычислять по формуле Работа потенциальной силы равна разности значений потенциальной энергии движущейся точки в начальном и конечном её положениях. |
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 364. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 силы, приложенной в точке
силы, приложенной в точке  , вычисляется по формуле
, вычисляется по формуле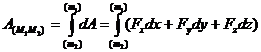 (4.33)
(4.33) . (4.34)
. (4.34) то
то или
или  . (4.35)
. (4.35) , (4.36)
, (4.36) ,
,  – значения силовой функции в точках
– значения силовой функции в точках  .
. , считая
, считая  при
при  , находим:
, находим: 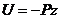 ;
; , считая
, считая  , находим:
, находим:  ;
; , откуда, считая
, откуда, считая  ,
, ,
, .
.
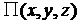 и
и  совпадающими. Тогда
совпадающими. Тогда  и согласно формуле (4.36)
и согласно формуле (4.36) ,
, ,
, . (4.37)
. (4.37)