
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Принцип сжимающих отображений.Ряд вопросов, связанных с существованием и единственностью решений уравнений того или иного типа (например, дифференциальных или алгебраических уравнений), можно сформулировать в виде вопроса о существовании и единственности неподвижной точки при некотором отображении соответствующего метрического пространства в себя. Среди различных критериев существования и единственности неподвижной точки притакого рода отображениях один из простейших и в то же время наиболее важных – так называемый принцип сжимающих отображений.
Точка x называется неподвижной точкой отображения A, если Ax=x. Иначе говоря, неподвижные точки – это решения уравнения Ax=x. Теорема. (Принцип сжимающих отображений). Всякое сжимающее отображение, определенное в полном метрическом пространстве M, имеет одну и только одну неподвижную точку. Доказательство. Пусть Воспользуемся неравенством треугольника, получим: Ρ( Так как α Положим Если Итак, существование неподвижной точки доказано. Докажем ее единственность. Если Ax=x,Ay=y, то (1) принимает вид ρ(x,y) Так как Теорема доказана. Уравнение Фредгольма с вырожденным ядром и невырожденным ядром  Ядро
Рассмотрим уравнение с таким ядром:
Пусть уравнение (2) имеет решение
Подставим (3) в (2) получим Решение интегрального уравнения с вырожденным ядром сводится к определению постоянных
тогда для
Если (6) не разрешима, то интегральное уравнение (2) не разрешимо. Пусть система (6) имеет решение Теоремы Фредгольма. Теорема1: данное однородное линейное уравнение 2 – го рода имеет и притом единственное решение при всякой функции f или соотв. Однородное уравнение имеет по крайней мере одно нетривиальное решение. Теорема 2 : если для данного уравнения (1) имеет число место случай альтернативы,то он имеет и два транспонированного уравнения. Z(x)= Причем как данное уравнение и транспонированное имеет конечное число линейно независима решения, и число это одинаково для обеих уравнений. Теорема3. Во втором случае альтернативы необходимым и достаточным условием сущ. решения неоднородного уравнения(1) явлю условие: Во физических задачах наряду с задачами в которых необход. найти наиб и наим. значение некоторой ф-ии встречаются задачи о максимуме и минимуме величин особого рода, наз-ых функционалом Под функционалом будем понимать переменную велечинуЮзначение которой опред-я выбором одной или нескольких ф-ийнапример,функционаломявл. длина l кривой y=y(x)соединяющей 2 заданные точки A( Исходя из приложеннейопред. Интеграла функционалом l,действ на ф-ю y=y(x): L[y(x)]= Вариационные исчисления изучает методы, позволяющие находить максимумы и минимумым значения для функционала abзадачах,где требуется исслед. Функционала на max и minназ-я вариационное исчисления. Лемма1 Если для каждой, непрерыв на отрезке( Где Ф-непр. На отрезке [x0,x],то Ф(х) = 0 на этом же отрезке. А необходим условием oxtrдифф-я ф-ииявлравенство:ɥ’|α,0=0 Поэтому необходимым условием oxtr функционала будет Или продифф-овFy-Fxy’-Fyy’*y’-Fy’y’*y’’=0 -----уравнение Эйлера. Задача о брахистохроне. В этой задаче требуется опред-тьлинию,соединяющую 2 две заданные точки а и б не лежащие на одной вертикальной прямой и обладают тем св-ом,что тело скатится по этой линии за кратчайшее время. Очевидно, что такой линией не будет прямой поскольку при движ-ние по прямой v будет нарастать сравнительно медленно.
|
|||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 407. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , что для любых двух точек
, что для любых двух точек  выполняется неравенство
выполняется неравенство  (1)
(1)
 -произвольная точка в M. Положим
-произвольная точка в M. Положим  Покажем, что последовательность
Покажем, что последовательность  фундаментальная. Действительно, считая для определенности
фундаментальная. Действительно, считая для определенности  , имеем
, имеем 

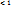 , то при достаточно большом n эта величина сколь угодно мала. В силу полноты M последовательность
, то при достаточно большом n эта величина сколь угодно мала. В силу полноты M последовательность 
 , то в силу (1)
, то в силу (1)  . Поэтому
. Поэтому 


 , отсюда следует, что
, отсюда следует, что 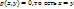
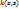 интегрального уравнения Фредгольма (2) называется вырожденным,если его можно представить в виде конечной суммы производных двух функций, одна из которых зависит от
интегрального уравнения Фредгольма (2) называется вырожденным,если его можно представить в виде конечной суммы производных двух функций, одна из которых зависит от  , а другая от
, а другая от 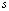 :
: (1)
(1)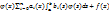 (2)
(2) - непрерывная на
- непрерывная на  функция.
функция. , тогда обозначим через
, тогда обозначим через (3)
(3)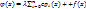 (4)
(4) . Заменим в (4) i на j, умножим обе части (4) на
. Заменим в (4) i на j, умножим обе части (4) на  и проинтегрируем правую и левую части по x от a до b:
и проинтегрируем правую и левую части по x от a до b: (5)
(5) воспользуемся (3), получим из (5) систему линейных алгебраических уравнений, которым должны удовлетворять коэффициенты
воспользуемся (3), получим из (5) систему линейных алгебраических уравнений, которым должны удовлетворять коэффициенты 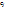 :
: (6)
(6) , тогда подставив в (4), получим
, тогда подставив в (4), получим  (ᶓ ,x)Z(ᶓ)dᶓ+f(x) (8)
(ᶓ ,x)Z(ᶓ)dᶓ+f(x) (8) (x)Z(x)dx=0,где Z- любое решение транспанированного уравнения(8)
(x)Z(x)dx=0,где Z- любое решение транспанированного уравнения(8) )и B(
)и B(  )
) dx
dx ) ф-ии η(x) интеграл
) ф-ии η(x) интеграл  (x)y(x)dx=0
(x)y(x)dx=0 -
-  (Fy’))δydx=0
(Fy’))δydx=0