
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Исследование устойчивости решения по первому приближению.Рассмотрим линейную систему дифференциальных уравнений n-го порядка:
Линейная система устойчива по Ляпунову при t ≥ t0, если каждое её решение x = φ(t) устойчиво по Ляпунову при t ≥ t0.
Линейная система асимптотически устойчива по Ляпунову при t → ∞ , если каждое её решение x = φ(t) устойчиво по Ляпунову при t → ∞ . Решения линейной системы либо все одновременно устойчивы, либо все неустойчивы. Справедливы следующие утверждения. Теорема об устойчивости решений линейной системы дифференциальных уравнений.Пусть в неоднородной линейной системе x' = A(t)x + b(t) матрица A(t) и вектор-функция b(t) непрерывны на промежутке [t0 , ∞). Система устойчива при t ≥ t0, тогда и только тогда, когда тривиальное решение x = 0 однородной системы x' = A(t) x устойчиво при t ≥ t0. Теорема об асимптотической устойчивости решений линейной системы дифференциальных уравнений.Пусть в неоднородной линейной системе x' = A(t)x + b(t) матрица A(t) и вектор-функция b(t) непрерывны на промежутке [t0 , ∞). Система асимптотически устойчива при t → ∞, тогда и только тогда, когда тривиальное решение x = 0 (точка покоя) однородной системы x' = A(t)x асимптотически устойчиво при t → ∞.
Эти утверждения означают, что для исследования устойчивости линейной системы достаточно исследовать устойчивость точки покоя соответствующей однородной системы. Рассмотрим автономную систему второго порядка: Обозначим  Точка a, в которой правая часть системы обращается в нуль, называется положением равновесия системы. Положение равновесия называют также точкой покоя автономной системы. Точка покоя a называетсяустойчивой по Ляпунову, если: Очевидно, что линейная автономная система если l1 и l2— действительные отрицательные числа, то точка покоя устойчива и называется устойчивым узлом если l1 и l2 — действительные положительные числа, то точка покоя неустойчива и называется неустойчивым узлом если l1 и l2 — действительные числа, имеющие разные знаки, то точка покоя неустойчива и называется седлом если l1 и l2 — комплексные числа, l1,2 =Rell ± Imll и Rel не превышает нуля, то точка покоя устойчива, точнее, при Rel =0 точка устойчива, но не асимптотически устойчива и называется центром, при Rel< 0 она асимптотически устойчива и называется устойчивым фокусома если Rel>0, то точка покоя неустойчива и называется неустойчивым фокусом
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 231. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


 и
и 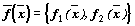 .
. — решение автономной системы второго порядка. Тогда уравнения
— решение автономной системы второго порядка. Тогда уравнения 
 при
при  существует решение задачи Коши с начальным условиям
существует решение задачи Коши с начальным условиям 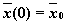 ;
;  , что если
, что если  и
и  при всех
при всех  при достаточно малых
при достаточно малых  .
.
