
Студопедия
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
|
Задача об изогональных траекториях.
К уравнениям , не разрешенным относительно производной,приводят чаще всего различные геометрические задачи,на примере задачоб изогональных траекториях
.Если : F(x,y,a)=0 (1)
Однопараметрическое семейство кривых, где a-параметр, то его изогональной траекторией называется другое семейство кривых , пересекающихся с кривыми семейства(1) под одним и тем же углом φ.В частности, если этот угол прямой , то траектория называется ортогональной.
Составим дифференциальное уравнение заданного семейства кривых (1).для этого продифференцируем по x уравнение(1) ,получим :  .(2) .(2)
Исключим параметр a из уравнения (1) и (2). Допустим ,что при этом дифференциальное уравнения семейства(1) имеет вид : y’=f(x,y). (3)

Угол мехду двумя кривыми в их точке пересечения М(х,у) называется угол между касательными , проведенными к кривым в этой точке. Если обозначить через α угол ,образованный с осью Ох касательной к кривой I семейства(1) в точке М ,а через β –угол ,образованный с осью Ох касательной к кривой II искомого семейства в этой же точке М,
то φ=±( β-a) или β=φ ±a . отсюда следует , что : tg β=  . .
Величина tg  задана , обозначим ее через k ; tga=y’=f(x,y) ; мы получили соотношение между координатами любой точки изогональной траектории и угловым коэффициентом касательной в этой точке ,т.е. дифференциальное уравнение семейства траекторий. Обозначим tg β через y’ ; тогда : tg = y’= задана , обозначим ее через k ; tga=y’=f(x,y) ; мы получили соотношение между координатами любой точки изогональной траектории и угловым коэффициентом касательной в этой точке ,т.е. дифференциальное уравнение семейства траекторий. Обозначим tg β через y’ ; тогда : tg = y’=  . .
Общий интеграл этого дифференциального уравнения является уравнение семейства изогональных траекторий семейства кривых(1) ; они пересекают кривые (1) под одним и тем же углом φ.
Итак , мы имеем правило : чтобы получить дифференциальное уравнение семейства изогональных траекторий данного семейства кривых (1) ,надо в дифференциальном уравнении (3) этого семейства заменить y’ на 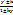 , где к- тангенс угла пересечения кривых с траекториями. В частности ,для ортогональных траекторий надо заменить y’ на -- , где к- тангенс угла пересечения кривых с траекториями. В частности ,для ортогональных траекторий надо заменить y’ на --  . .
11. дифференциалые уравнения высших порядков .начальные условия.
F (x; y; y’;…;y(n)) – дифференциальное уравнение n – порядка или y(n) = f(x; y; y’; …; y(n-1)) Общим решением этого уравнения является: y = j(x; c1; c2;…; cn)Для дифференциального уравнения n – порядка имеет место теорема Коши о существовании и единственности частного решения уравнения при данных n – начальных условиях. Например для дифференциального уравнения второго порядка. Теорема Коши: y``=f(x,y,y`)начальные условия: x=  y( y(  )=y0, y`(x0)=y`0. Если f(x,y,y`)непрерывна в точке (x0,y0,y`0)и в этой точке непрерывна частная производная f`y`, то существует, причём единственное частное решение, удовлетворяющее данным начальным условиям .y*= φ (x,C*1,C*2) )=y0, y`(x0)=y`0. Если f(x,y,y`)непрерывна в точке (x0,y0,y`0)и в этой точке непрерывна частная производная f`y`, то существует, причём единственное частное решение, удовлетворяющее данным начальным условиям .y*= φ (x,C*1,C*2)
12.теорема существования и динствености решения дифференциалые уравнения высших порядков .
Задачей Коши для ДУ n -го порядка называется задача отыскания его частного решения у = у(х), которое удовлетворяет начальным условиям:y(x0)=y0;y`(x0)=y`0;y``(x0)=y``0;…;y(n-1)0(x0)=y(n-1), где x0,y`0.y``0…..y(n-10 заданные числаТаким образом, решение задачи Коши для ДУ n -го порядка сводится к нахождению интегральной кривой, проходящей через точку M0(x0,y0,y`0.y``0…..y(n-10 ) из области определения (D ) функции f(x,y,y`0,y``,..,y(n-1))
Теорема.Задача Коши для ДУ n -го порядка имеет единственное решение, если:
f(x,y,y`0,y``,..,y(n-1)) непрерывна в области D ;
 , ,  , ,  ,…, ,…,  непрерывны в областиD. непрерывны в областиD.
В этом случае решение ДУ n -го порядка проходит через заданную точку M0(x0,y0,y`0.y``0…..y(n-10 )
13. методы понижения порядка уравнения
1. Уравнения, не содержащие искомой функции и нескольких последовательных производных.Рассмотрим уравнения вида F(x,y(k),y(k-1),…,y(n))=0 (1≤k≤n).С помощью замены y(k)=u(x), где u - новая неизвестная функция, уравнение приводится к уравнению (n-k) -го порядка:F(x,u,u`,…,u(n-k))=0
2. Уравнения, не содержащие явно независимой переменной. Рассмотрим уравнения вида F(y,y`,..,y(n))=0 С помощью замены y`=p,(где p=p(y) - новая искомая функция независимая переменная) порядок уравнения понижается на единицу, так как
Y``=  = =  =pp`y```= =pp`y```=  = =  =(p``p+p`2)pДанная подстановка дает уравнение (n-1) - го порядка относительно новой неизвестной функции p:F1(y,p,p`,..,p(n-1))=0 При осуществлении такой замены возможна потеря решения y=const. Непосредственной подстановкой необходимо проверить наличие у уравнения решений такого вида. =(p``p+p`2)pДанная подстановка дает уравнение (n-1) - го порядка относительно новой неизвестной функции p:F1(y,p,p`,..,p(n-1))=0 При осуществлении такой замены возможна потеря решения y=const. Непосредственной подстановкой необходимо проверить наличие у уравнения решений такого вида.
14.понятие первого интеграла.
Зада́ча Коши́ — одна из основных задач теории дифференциальных уравнений (обыкновенных и с частными производными); состоит в нахождении решения (интеграла) дифференциального уравнения, удовлетворяющего так называемым начальным условиям .Задача Коши обычно возникает при анализе процессов, определяемых дифференциальным законом эволюции и начальным состоянием (математическим выражением которых и являются уравнение и начальное условие). Этим мотивируется терминология и выбор обозначений: начальные данные задаются при t=0, а решение отыскивается при t>0.От краевых задач задача Коши отличается тем, что область, в которой должно быть определено искомое решение, здесь заранее не указывается. Тем не менее, задачу Коши можно рассматривать как одну из краевых задач.Основные вопросы, которые связаны с задачей Коши, таковы:
Существует ли (хотя бы локально) решение задачи Коши?
Если решение существует, то какова область его существования?
Является ли решение единственным?
Если решение единственно, то будет ли оно корректным, то есть непрерывным (в каком-либо смысле) относительно начальных данных?
Говорят, что задача Коши имеет единственное решение, если она имеет решение y=f(t)и никакое другое решение не отвечает интегральной кривой, которая в сколь угодно малой выколотой окрестности точки (x0,y0)имеет поле направлений, совпадающее с полем направлений y=f(t). Точка (x0,y0)задаёт начальные условия.
15 Линейные однородные с частными.
ур-ие  ( ( 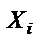 - данные функции аргументов - данные функции аргументов  , определены в , определены в  , ,  - искомая функция) – линейное однородное с частными. Решением будет ифференцируемаяпо - искомая функция) – линейное однородное с частными. Решением будет ифференцируемаяпо  , которая при подстановке в исходное превращает его в тождество. Геометрически решение: поверхность в пр-ве переменных x, u (интегральная п-ть). Систему обычных диффуров, соответствующую ур-ию (1) , которая при подстановке в исходное превращает его в тождество. Геометрически решение: поверхность в пр-ве переменных x, u (интегральная п-ть). Систему обычных диффуров, соответствующую ур-ию (1) 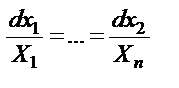 (2) - называют системой в симметричной форме. (2) в силу условий, наложенных на коэффициенты (1), можно записать в нормальной форме (2) - называют системой в симметричной форме. (2) в силу условий, наложенных на коэффициенты (1), можно записать в нормальной форме  (3).Рассм. в области единственности общее решение этой системы: (3).Рассм. в области единственности общее решение этой системы:  если удаётся разрешить эти ур-ияотн-но если удаётся разрешить эти ур-ияотн-но  . Получим . Получим  (4) – каждое из этих ур-ий называется первым интегралом системы (3), а каждая из функций (4) – каждое из этих ур-ий называется первым интегралом системы (3), а каждая из функций 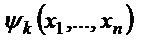 - интегралом этой же системы. Интегральные кривые системы ур-ий (2) или (3) называют х-ми ур-ия с частными производными (1). Связь между решениями ур-ия (1) и интегралами соответствующей системы обычныхдиффуров (3) или (2): Т1. Если - интегралом этой же системы. Интегральные кривые системы ур-ий (2) или (3) называют х-ми ур-ия с частными производными (1). Связь между решениями ур-ия (1) и интегралами соответствующей системы обычныхдиффуров (3) или (2): Т1. Если  - интеграл системы (2) или (3), то - интеграл системы (2) или (3), то  - решение (1). Т2. Если - решение (1). Т2. Если  - решение(1), то - решение(1), то  - интеграл(3). Т3. Общим решением (1), т.е. решением, которое вмещает все без исключения решения этого ур-ия, является - интеграл(3). Т3. Общим решением (1), т.е. решением, которое вмещает все без исключения решения этого ур-ия, является  - произвольная дифференцируемая функция. Задачей Коши для (1) наз-ся задача о нахождении решения - произвольная дифференцируемая функция. Задачей Коши для (1) наз-ся задача о нахождении решения  , ,  этого ур-ия, которое удовлетворяет условию этого ур-ия, которое удовлетворяет условию  , где , где  - гладкая гиперповерхность, а - гладкая гиперповерхность, а  - начальное условие. Построение решения (1) с нач. условием - начальное условие. Построение решения (1) с нач. условием  : 1. находим базис первых интегралов : 1. находим базис первых интегралов  системы в симметричной форме (2), соответствующей исходному (1). 2. Составляем систему функциональных ур-ий системы в симметричной форме (2), соответствующей исходному (1). 2. Составляем систему функциональных ур-ий  которую разрешаем относительно которую разрешаем относительно  : :  3. строим функцию 3. строим функцию  4. Выписываем искомое решение по формуле 4. Выписываем искомое решение по формуле  и если возможно проводим аналитическое упрощение. и если возможно проводим аналитическое упрощение.
 17. Существование и единственность решения задачи Коши для уравнений с частными производными первого порядка 17. Существование и единственность решения задачи Коши для уравнений с частными производными первого порядка
.Если первая часть уравнения  непрерывна в замкнутой области D, а непрерывна в замкнутой области D, а  (ограниченная) и удовлетворяет в D условию Липшица (ограниченная) и удовлетворяет в D условию Липшица  , где L – константа Липшица, а , где L – константа Липшица, а  и и 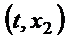 - две любые точки из D, то - две любые точки из D, то  решение уравнения, удовлетворяющее начальному условию решение уравнения, удовлетворяющее начальному условию  и это решение определяет и непрерывно дифференцируемое в интервале и это решение определяет и непрерывно дифференцируемое в интервале 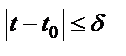 , где , где 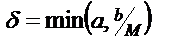 и не выходитпри этих значениях t из области D и не выходитпри этих значениях t из области D  . Решение задачи Коши при выполнении условий теоремы можно найти как предел при . Решение задачи Коши при выполнении условий теоремы можно найти как предел при  равномерно сходящейся последовательности функций равномерно сходящейся последовательности функций  , определённых рекуррентным соотношением , определённых рекуррентным соотношением  , n=1, 2, …, , n=1, 2, …,  . Если f имеет в D ограниченную частную производную . Если f имеет в D ограниченную частную производную 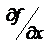 , то она автоматически удовлетворяет условию Липшица, а погрешность задаётся неравенством , то она автоматически удовлетворяет условию Липшица, а погрешность задаётся неравенством  , при , при  , ,  . Если правая часть f(t,x) непрерывная в области R2, но условию Липшица не удовлетворяет, то каждая задача Коши имеет решение (т-ме Пеано). Но решение не единственное. . Если правая часть f(t,x) непрерывная в области R2, но условию Липшица не удовлетворяет, то каждая задача Коши имеет решение (т-ме Пеано). Но решение не единственное.
18. Линейные дифференциальные уравнения. Область существования решения. Общие свойства решений.
Под линейным дифф. ур-ем будем понимать ур-е вида:
 - (1), т.е. дифф. ур-е линейно относит. у и ее производных.Если - (1), т.е. дифф. ур-е линейно относит. у и ее производных.Если  ,то ур-е однородное,в противном случае-неоднородное. Если коэфф. ,то ур-е однородное,в противном случае-неоднородное. Если коэфф.  в любой точке х окрестности [а,b]: в любой точке х окрестности [а,b]:  , ,  ур-е,разрешенное относительно старшей производной,а значит можем применить к нему теорему о ед.сущ. реш-я задачи Коши.Вчастности,если коэффициенты ур-е,разрешенное относительно старшей производной,а значит можем применить к нему теорему о ед.сущ. реш-я задачи Коши.Вчастности,если коэффициенты  (x) непрерывны на [а,b],то в окрестности любых начальных значениях:у( (x) непрерывны на [а,b],то в окрестности любых начальных значениях:у(  )= )=  , у’( , у’(  )= )=  ’,…, ’,…,  ( (  )= )= 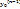 где где  -произвольная точка интервала [а,b]. Заметим,что линейность ур-я и однородность сохраняются при любом преобразовании независимого и зависимого переменного. Линейное однородное ур-е: -произвольная точка интервала [а,b]. Заметим,что линейность ур-я и однородность сохраняются при любом преобразовании независимого и зависимого переменного. Линейное однородное ур-е:  запишем более кратко: L[y]=0 ,где L имеет вид: запишем более кратко: L[y]=0 ,где L имеет вид:
L=  . Будем наз-ть L- линейным дифф-ым оператором. Он обладает след сво-ми: 1) L[c,y]=cL[y]; 2)L[y1+y2]=L[y1]+L[y2]. . Будем наз-ть L- линейным дифф-ым оператором. Он обладает след сво-ми: 1) L[c,y]=cL[y]; 2)L[y1+y2]=L[y1]+L[y2].
19. Линейная зависимость функций. Определитель Вронского. Фундаментальная система решений. Общее решение, Формула Остроградского-Лиувилля.
Ф-ии у1,у2,….уnназ-я линейно зависимыми на отрезке [а,b],если сущ-ют постоянные величины  такие,что на этом отрезке такие,что на этом отрезке 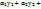 …+ …+ 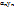 =0, причем хотя бы одно =0, причем хотя бы одно  , если же на отрезке [а,b] рав-о справедливо только при , если же на отрезке [а,b] рав-о справедливо только при  ,то ф-ии у1,у2,….уnназ-я линейно независимыми ,то ф-ии у1,у2,….уnназ-я линейно независимыми
Если определитель =0,то ф-я линейно зависима и наоборот.
Опред.Общим решением на [а,b] линейного однородного ур-я:
 с непрерывными на этом отрезке коэфф.явл.линейная комбинация: y(x)= с непрерывными на этом отрезке коэфф.явл.линейная комбинация: y(x)=  и линейно независима на том отрезке частных производных и линейно независима на том отрезке частных производных  с произвольными постоянными. с произвольными постоянными.
Опред. любое n линейно независимых частных реш-ий линейного однородного ур-я n-го порядка наз-я его фундаментальной системой реш-я. Для построения фундаментальной системы решения необходимо взять n квадрат чисел с одним лишь требованием: 
Тогда в качестве частных реш-ий фундаментальной системы реш-ий достаточно взять реш-е задачи коши с начальными данными
Формула Остроградского-Лиувилля 
20. Неоднородные линейные уравнения. Методы Лагранжа и Коши нахождения частного решения неоднородного уравнения.
Линейное неоднородное ур-е можно записать в виде:  + +  , где , где 
Метод Лагранжа решения неоднородных линейных дифференциальных уравнений еще называют методом вариации произвольной постоянной. Так реш-е неоднородного ур-я L[y]=f(x) ищем в виде суммы:
y(x)=  . Алгебраическая,линейная система ур-ий относительно неизвестной . Алгебраическая,линейная система ур-ий относительно неизвестной  записывается в виде: записывается в виде:  - Проинтегрировав данную систему найдем - Проинтегрировав данную систему найдем  и подставим в (1) получим общее реш-е неоднородного ур-я. и подставим в (1) получим общее реш-е неоднородного ур-я.
21. Линейные уравнения с постоянными коэффициентами. Нахождение фундаментальной системы решений однородного уравнения.
Рассм.  , где коэффициенты действительные числа. Необходимо составить характеристическое уравнения с помощью замены производных , где коэффициенты действительные числа. Необходимо составить характеристическое уравнения с помощью замены производных  искомой функции степенями искомой функции степенями  и найти все его корни. Каждому действительному корню и найти все его корни. Каждому действительному корню 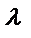 кратности kхарактеристическогоур-ия кратности kхарактеристическогоур-ия  , соответствуют k линейно независимых решений ур-ия: , соответствуют k линейно независимых решений ур-ия:  , а каждой паре комплексных корней , а каждой паре комплексных корней  , кратности s соответствуют s пар линейно независимых решений: , кратности s соответствуют s пар линейно независимых решений:  , и тоже, только с sin. Т.О., если характеристическое ур-ие имеет m действительных корней , и тоже, только с sin. Т.О., если характеристическое ур-ие имеет m действительных корней  , кратности , кратности  и l пар комплексно сопряжённых корней и l пар комплексно сопряжённых корней 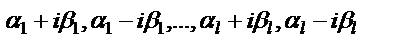 , кратностей , кратностей  , ( , (  . .
Линейной системой называют вида:  , в матричной форме , в матричной форме  : :  , ,  , ,
Св-ва: 1. если  - непрерывны, то - непрерывны, то  решение, удовлетворяющее решение, удовлетворяющее  , оно будет непрерывным и определённым в рассм. интервале. Свойства: 1. Если , оно будет непрерывным и определённым в рассм. интервале. Свойства: 1. Если  . То в силу единственности . То в силу единственности  . 2. Если . 2. Если  , где , где  , то , то  (*) - решение. Векторные функции (*) - решение. Векторные функции  называют линейно независимыми, если называют линейно независимыми, если  числа, одновременно не равные нулю… ну и короче бля линейная комбинация их равна нулю. Допустим числа, одновременно не равные нулю… ну и короче бля линейная комбинация их равна нулю. Допустим  - решение системы. Создадим матрицу столбцами которой являются эти решения - решение системы. Создадим матрицу столбцами которой являются эти решения  . Т1. Если . Т1. Если 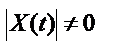 хотя бы где-нить, то эти решения линейно независимые else зависимые. Т2. Система имеет n линейно независимых решений. Общее решение: хотя бы где-нить, то эти решения линейно независимые else зависимые. Т2. Система имеет n линейно независимых решений. Общее решение:  . Совокупность решений – фундаментальная система (базис). . Совокупность решений – фундаментальная система (базис).
22. Неоднородные линейные дифференциальные уравнения. Общее решение.
Общее решение  находится находится  , где , где  - какое-нить частное решение, - какое-нить частное решение,  - общее решение соответствующего однородного. Если известна система решений однородного ур-ия, то общее решение неоднородного может быть найдено с помощью метода вариации. Ищем общее решение в виде - общее решение соответствующего однородного. Если известна система решений однородного ур-ия, то общее решение неоднородного может быть найдено с помощью метода вариации. Ищем общее решение в виде  , тогда для функций C получим систему , тогда для функций C получим систему  система имеет единственное решение относительно система имеет единственное решение относительно  . Если правая часть неоднородно есть сумма нескольких функций . Если правая часть неоднородно есть сумма нескольких функций  и и  - некоторые частные решения ур-ий - некоторые частные решения ур-ий  ( (  - левая часть), соответственно, то сумма - левая часть), соответственно, то сумма  - частное решение исх. ур-ия. - частное решение исх. ур-ия.
|


 .(2)
.(2)
 .
. задана , обозначим ее через k ; tga=y’=f(x,y) ; мы получили соотношение между координатами любой точки изогональной траектории и угловым коэффициентом касательной в этой точке ,т.е. дифференциальное уравнение семейства траекторий. Обозначим tg β через y’ ; тогда : tg = y’=
задана , обозначим ее через k ; tga=y’=f(x,y) ; мы получили соотношение между координатами любой точки изогональной траектории и угловым коэффициентом касательной в этой точке ,т.е. дифференциальное уравнение семейства траекторий. Обозначим tg β через y’ ; тогда : tg = y’=  .
.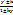 , где к- тангенс угла пересечения кривых с траекториями. В частности ,для ортогональных траекторий надо заменить y’ на --
, где к- тангенс угла пересечения кривых с траекториями. В частности ,для ортогональных траекторий надо заменить y’ на --  .
. y(
y(  )=y0, y`(x0)=y`0. Если f(x,y,y`)непрерывна в точке (x0,y0,y`0)и в этой точке непрерывна частная производная f`y`, то существует, причём единственное частное решение, удовлетворяющее данным начальным условиям .y*= φ (x,C*1,C*2)
)=y0, y`(x0)=y`0. Если f(x,y,y`)непрерывна в точке (x0,y0,y`0)и в этой точке непрерывна частная производная f`y`, то существует, причём единственное частное решение, удовлетворяющее данным начальным условиям .y*= φ (x,C*1,C*2) ,
,  ,
,  ,…,
,…,  непрерывны в областиD.
непрерывны в областиD. =
=  =pp`y```=
=pp`y```=  =
=  =(p``p+p`2)pДанная подстановка дает уравнение (n-1) - го порядка относительно новой неизвестной функции p:F1(y,p,p`,..,p(n-1))=0 При осуществлении такой замены возможна потеря решения y=const. Непосредственной подстановкой необходимо проверить наличие у уравнения решений такого вида.
=(p``p+p`2)pДанная подстановка дает уравнение (n-1) - го порядка относительно новой неизвестной функции p:F1(y,p,p`,..,p(n-1))=0 При осуществлении такой замены возможна потеря решения y=const. Непосредственной подстановкой необходимо проверить наличие у уравнения решений такого вида. (
( 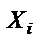 - данные функции аргументов
- данные функции аргументов  , определены в
, определены в  ,
,  - искомая функция) – линейное однородное с частными. Решением будет ифференцируемаяпо
- искомая функция) – линейное однородное с частными. Решением будет ифференцируемаяпо 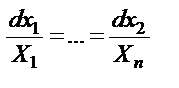 (2) - называют системой в симметричной форме. (2) в силу условий, наложенных на коэффициенты (1), можно записать в нормальной форме
(2) - называют системой в симметричной форме. (2) в силу условий, наложенных на коэффициенты (1), можно записать в нормальной форме  (3).Рассм. в области единственности общее решение этой системы:
(3).Рассм. в области единственности общее решение этой системы:  если удаётся разрешить эти ур-ияотн-но
если удаётся разрешить эти ур-ияотн-но  . Получим
. Получим  (4) – каждое из этих ур-ий называется первым интегралом системы (3), а каждая из функций
(4) – каждое из этих ур-ий называется первым интегралом системы (3), а каждая из функций 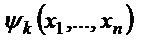 - интегралом этой же системы. Интегральные кривые системы ур-ий (2) или (3) называют х-ми ур-ия с частными производными (1). Связь между решениями ур-ия (1) и интегралами соответствующей системы обычныхдиффуров (3) или (2): Т1. Если
- интегралом этой же системы. Интегральные кривые системы ур-ий (2) или (3) называют х-ми ур-ия с частными производными (1). Связь между решениями ур-ия (1) и интегралами соответствующей системы обычныхдиффуров (3) или (2): Т1. Если  - интеграл системы (2) или (3), то
- интеграл системы (2) или (3), то  - решение (1). Т2. Если
- решение (1). Т2. Если  - решение(1), то
- решение(1), то  - интеграл(3). Т3. Общим решением (1), т.е. решением, которое вмещает все без исключения решения этого ур-ия, является
- интеграл(3). Т3. Общим решением (1), т.е. решением, которое вмещает все без исключения решения этого ур-ия, является  - произвольная дифференцируемая функция. Задачей Коши для (1) наз-ся задача о нахождении решения
- произвольная дифференцируемая функция. Задачей Коши для (1) наз-ся задача о нахождении решения  ,
,  этого ур-ия, которое удовлетворяет условию
этого ур-ия, которое удовлетворяет условию  , где
, где  - гладкая гиперповерхность, а
- гладкая гиперповерхность, а  - начальное условие. Построение решения (1) с нач. условием
- начальное условие. Построение решения (1) с нач. условием  : 1. находим базис первых интегралов
: 1. находим базис первых интегралов  системы в симметричной форме (2), соответствующей исходному (1). 2. Составляем систему функциональных ур-ий
системы в симметричной форме (2), соответствующей исходному (1). 2. Составляем систему функциональных ур-ий  которую разрешаем относительно
которую разрешаем относительно  :
:  3. строим функцию
3. строим функцию  4. Выписываем искомое решение по формуле
4. Выписываем искомое решение по формуле  и если возможно проводим аналитическое упрощение.
и если возможно проводим аналитическое упрощение. 17. Существование и единственность решения задачи Коши для уравнений с частными производными первого порядка
17. Существование и единственность решения задачи Коши для уравнений с частными производными первого порядка непрерывна в замкнутой области D, а
непрерывна в замкнутой области D, а  (ограниченная) и удовлетворяет в D условию Липшица
(ограниченная) и удовлетворяет в D условию Липшица  , где L – константа Липшица, а
, где L – константа Липшица, а  и
и 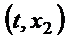 - две любые точки из D, то
- две любые точки из D, то  решение уравнения, удовлетворяющее начальному условию
решение уравнения, удовлетворяющее начальному условию  и это решение определяет и непрерывно дифференцируемое в интервале
и это решение определяет и непрерывно дифференцируемое в интервале 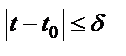 , где
, где 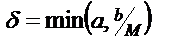 и не выходитпри этих значениях t из области D
и не выходитпри этих значениях t из области D  . Решение задачи Коши при выполнении условий теоремы можно найти как предел при
. Решение задачи Коши при выполнении условий теоремы можно найти как предел при  равномерно сходящейся последовательности функций
равномерно сходящейся последовательности функций  , определённых рекуррентным соотношением
, определённых рекуррентным соотношением  , n=1, 2, …,
, n=1, 2, …,  . Если f имеет в D ограниченную частную производную
. Если f имеет в D ограниченную частную производную 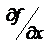 , то она автоматически удовлетворяет условию Липшица, а погрешность задаётся неравенством
, то она автоматически удовлетворяет условию Липшица, а погрешность задаётся неравенством  , при
, при  ,
,  . Если правая часть f(t,x) непрерывная в области R2, но условию Липшица не удовлетворяет, то каждая задача Коши имеет решение (т-ме Пеано). Но решение не единственное.
. Если правая часть f(t,x) непрерывная в области R2, но условию Липшица не удовлетворяет, то каждая задача Коши имеет решение (т-ме Пеано). Но решение не единственное. - (1), т.е. дифф. ур-е линейно относит. у и ее производных.Если
- (1), т.е. дифф. ур-е линейно относит. у и ее производных.Если  ,то ур-е однородное,в противном случае-неоднородное. Если коэфф.
,то ур-е однородное,в противном случае-неоднородное. Если коэфф.  в любой точке х окрестности [а,b]:
в любой точке х окрестности [а,b]:  ,
,  ур-е,разрешенное относительно старшей производной,а значит можем применить к нему теорему о ед.сущ. реш-я задачи Коши.Вчастности,если коэффициенты
ур-е,разрешенное относительно старшей производной,а значит можем применить к нему теорему о ед.сущ. реш-я задачи Коши.Вчастности,если коэффициенты  (x) непрерывны на [а,b],то в окрестности любых начальных значениях:у(
(x) непрерывны на [а,b],то в окрестности любых начальных значениях:у(  )=
)=  , у’(
, у’(  (
( 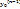 где
где  запишем более кратко: L[y]=0 ,где L имеет вид:
запишем более кратко: L[y]=0 ,где L имеет вид: . Будем наз-ть L- линейным дифф-ым оператором. Он обладает след сво-ми: 1) L[c,y]=cL[y]; 2)L[y1+y2]=L[y1]+L[y2].
. Будем наз-ть L- линейным дифф-ым оператором. Он обладает след сво-ми: 1) L[c,y]=cL[y]; 2)L[y1+y2]=L[y1]+L[y2]. такие,что на этом отрезке
такие,что на этом отрезке 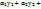 …+
…+ 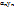 =0, причем хотя бы одно
=0, причем хотя бы одно  , если же на отрезке [а,b] рав-о справедливо только при
, если же на отрезке [а,b] рав-о справедливо только при  ,то ф-ии у1,у2,….уnназ-я линейно независимыми
,то ф-ии у1,у2,….уnназ-я линейно независимыми и линейно независима на том отрезке частных производных
и линейно независима на том отрезке частных производных  с произвольными постоянными.
с произвольными постоянными.

 +
+  , где
, где 
 . Алгебраическая,линейная система ур-ий относительно неизвестной
. Алгебраическая,линейная система ур-ий относительно неизвестной  записывается в виде:
записывается в виде:  - Проинтегрировав данную систему найдем
- Проинтегрировав данную систему найдем  и подставим в (1) получим общее реш-е неоднородного ур-я.
и подставим в (1) получим общее реш-е неоднородного ур-я. , где коэффициенты действительные числа. Необходимо составить характеристическое уравнения с помощью замены производных
, где коэффициенты действительные числа. Необходимо составить характеристическое уравнения с помощью замены производных  искомой функции степенями
искомой функции степенями  и найти все его корни. Каждому действительному корню
и найти все его корни. Каждому действительному корню 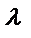 кратности kхарактеристическогоур-ия
кратности kхарактеристическогоур-ия  , соответствуют k линейно независимых решений ур-ия:
, соответствуют k линейно независимых решений ур-ия:  , а каждой паре комплексных корней
, а каждой паре комплексных корней  , кратности s соответствуют s пар линейно независимых решений:
, кратности s соответствуют s пар линейно независимых решений:  , и тоже, только с sin. Т.О., если характеристическое ур-ие имеет m действительных корней
, и тоже, только с sin. Т.О., если характеристическое ур-ие имеет m действительных корней  , кратности
, кратности  и l пар комплексно сопряжённых корней
и l пар комплексно сопряжённых корней 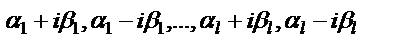 , кратностей
, кратностей  , (
, (  .
. , в матричной форме
, в матричной форме  :
:  ,
,  ,
, - непрерывны, то
- непрерывны, то  решение, удовлетворяющее
решение, удовлетворяющее  , оно будет непрерывным и определённым в рассм. интервале. Свойства: 1. Если
, оно будет непрерывным и определённым в рассм. интервале. Свойства: 1. Если  . То в силу единственности
. То в силу единственности  . 2. Если
. 2. Если  , где
, где  , то
, то  (*) - решение. Векторные функции
(*) - решение. Векторные функции  числа, одновременно не равные нулю… ну и короче бля линейная комбинация их равна нулю. Допустим
числа, одновременно не равные нулю… ну и короче бля линейная комбинация их равна нулю. Допустим  - решение системы. Создадим матрицу столбцами которой являются эти решения
- решение системы. Создадим матрицу столбцами которой являются эти решения  . Т1. Если
. Т1. Если 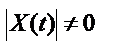 хотя бы где-нить, то эти решения линейно независимые else зависимые. Т2. Система имеет n линейно независимых решений. Общее решение:
хотя бы где-нить, то эти решения линейно независимые else зависимые. Т2. Система имеет n линейно независимых решений. Общее решение:  . Совокупность решений – фундаментальная система (базис).
. Совокупность решений – фундаментальная система (базис). находится
находится  , где
, где  - какое-нить частное решение,
- какое-нить частное решение,  - общее решение соответствующего однородного. Если известна система решений однородного ур-ия, то общее решение неоднородного может быть найдено с помощью метода вариации. Ищем общее решение в виде
- общее решение соответствующего однородного. Если известна система решений однородного ур-ия, то общее решение неоднородного может быть найдено с помощью метода вариации. Ищем общее решение в виде  , тогда для функций C получим систему
, тогда для функций C получим систему  система имеет единственное решение относительно
система имеет единственное решение относительно  . Если правая часть неоднородно есть сумма нескольких функций
. Если правая часть неоднородно есть сумма нескольких функций  и
и  - некоторые частные решения ур-ий
- некоторые частные решения ур-ий  (
(  - левая часть), соответственно, то сумма
- левая часть), соответственно, то сумма  - частное решение исх. ур-ия.
- частное решение исх. ур-ия.