
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Уравнение с правой частью в виде квазиполинома. Зависимость решений от начальных данных.Если же решается уравнение с постоянными коэффициентами, более экономным может оказаться так называемый метод квазиполиномов, если правая часть уравнения имеет специальный вид. Определение.Квазиполиномом называют выражение вида В различных приложениях теории О.Д.У. правые части f(x) уравнений с постоянными коэффициентами часто имеют подобный вид. Например, если такая функция описывает вынуждающее воздействие на некоторую механическую систему, находящуюся в колебательном режиме, то такое воздействие может зависеть нелинейно от времени x (полиномы Ps и Qr), осциллировать с частотой q, и быть модулированным с амплитудойм Вначале рассмотрим частный случай, когда q= 0, то есть, квазиполином имеет вид a0
Сокращая равенство на экспоненту, приходим к уравнению, связывающему два многочлена, так как дифференцирование любого многочлена также приводит к многочлену. При этом, если ни одно из чисел – a0 Rs (x) = Ps(x) (3) (11.10)  двух многочленов одинаковой степени, причем коэффициенты многочлена Rs (x) линейно зависят от коэффициентов многочлена Теорема1:.Частное решение неоднородного уравнения (8.1) с постоянными коэффициентами и правой частью вида
24. Линейное уравнение Эйлера. Линейное дифференциальное уравнение Эйлера имеет вид
Частное решение однородного дифференциального уравнения Эйлера можно найти сразу в виде Неоднородное дифференциальное уравнение Эйлера можно решать методом вариации постоянных (предварительно необходимо найти общее решение соответствующего однородного уравнения). ИЛИ Уравнение (1) |
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 568. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
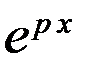 [Ps(x)cosqx + Qr(x)sinqx], где Ps(x) и Qr(x) - многочлены порядковs и t соответственно.
[Ps(x)cosqx + Qr(x)sinqx], где Ps(x) и Qr(x) - многочлены порядковs и t соответственно.
 . (1) . .
. (1) . .  y(x)=
y(x)= 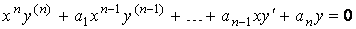 Будем искать частное решение уравнения (1) в виде квазиполинома: y(x)=
Будем искать частное решение уравнения (1) в виде квазиполинома: y(x)=  , где
, где 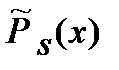 -многочлен того же порядка, что и Ps(x), но с неизвестными коэффициентами
-многочлен того же порядка, что и Ps(x), но с неизвестными коэффициентами  ,
,  ,
, 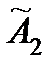 ,. . .
,. . .  . Подставляя искомое решение такого вида в (1), и пронося экспоненту через дифференциальный оператор, получим
. Подставляя искомое решение такого вида в (1), и пронося экспоненту через дифференциальный оператор, получим
 . . .
. . . 
 не обращается в ноль, степень многочлена в левой части остается равной s , так как у операторного многочлена слева сохраняется свободный член
не обращается в ноль, степень многочлена в левой части остается равной s , так как у операторного многочлена слева сохраняется свободный член
 . . .
. . . 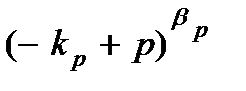 , отличный от нуля. В результате, получаем равенство
, отличный от нуля. В результате, получаем равенство cosqx +
cosqx +  sinqx], где t = max{s, r}, если ни один из корней характеристического уравнения (1.3) не совпадает с числами p±iq, и в виде
sinqx], где t = max{s, r}, если ни один из корней характеристического уравнения (1.3) не совпадает с числами p±iq, и в виде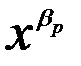 [
[  кратности bp.
кратности bp. Данное уравнение может быть сведено к линейному уравнению с постоянными коэффициентами при помощи замены независимой переменной
Данное уравнение может быть сведено к линейному уравнению с постоянными коэффициентами при помощи замены независимой переменной 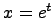 .
. , где
, где  -- некоторая постоянная. Для нахождения этой постоянной надо подставить решение в уравнение и решить получившееся характеристическое (алгебраическое) уравнение относительно
-- некоторая постоянная. Для нахождения этой постоянной надо подставить решение в уравнение и решить получившееся характеристическое (алгебраическое) уравнение относительно  ,
,  ,
,  ,...
,... 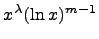 Каждой паре мнимых корней
Каждой паре мнимых корней  кратности m соответствует m пар частных решений
кратности m соответствует m пар частных решений  ,
,  ,
,  ,
,  ,...
,...