
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Теорема существования решения задачи Коши дифференциального уравнения первогоПорядка. Условие (2) называется начальным условием или условиями Коши. Под задачей Коши будем понимать задачу об отыскании решения уравнения (1) удовлетв.данным (2) Геометрически это означает, что из всего множества интегральных кривых нужно выделить ту интегральную кривую, которая проходит ч/з Естественно встаёт вопрос, есть ли вообще решение у уравнение (1), а если и есть, то сколько таких, удовл.условию (2). Теорема 1.(теорема существования единственности решения) – если функция f и её частная производная 4.Зависимость решений от начальных данных и от параметров. 1)одна удовл.уравнению (1) при 2)каковы бы ни были нач данные (2) всегда найдётся значение С0 постоянной С такое, что решение Всякое решение Неявное задание общего решения f(x,y,c)=0, где С произвольная constназобщим интегральным уравнением (1) Соотношение, которое получ из общего интеграла на конкретном значении С назчастным интегралом уравнения (1) 5 .Уравнение с разделяющими переменными Для его разрешения достаточно проинтегрировать неравенство (1)
Т.о. (2)есть общий интеграл уравнения (1). Уравнение вида:
Называется уравнением с разделяющимися переменными. Для его разрешения разделим неравенство (3) на произведение. 
Кот относится к классу уравнений с разделяющимися переменными, т.е. к классу уравнений вида (1), а значит выражение:
Заметим, что при делении уравнения на произведение Значит, чтобы найти особые решения уравнения (3) необходимо прировнять произведение к 0, т.е.
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 218. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (2)
(2) .
. непрерывна в области D, то решения дифф.уравнения (1), удовлетв.начальным условиям (2) существенно и единственно.
непрерывна в области D, то решения дифф.уравнения (1), удовлетв.начальным условиям (2) существенно и единственно. , зависящую от одной производной постоянной С и удовл. Следующим условиям:
, зависящую от одной производной постоянной С и удовл. Следующим условиям: допустимых значениях постоянной С.
допустимых значениях постоянной С. удовл.этим нач данным, т.е.
удовл.этим нач данным, т.е. 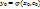
 при конкретном значении с=с0 назчастным решением уравнения (1).
при конкретном значении с=с0 назчастным решением уравнения (1). называется дифф уравнением с разделёнными переменными.
называется дифф уравнением с разделёнными переменными.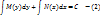

 получим:
получим: 
 есть общий интеграл уравнения (3).
есть общий интеграл уравнения (3). и проверить является ли корни уравнения решения для уравнения (3).
и проверить является ли корни уравнения решения для уравнения (3).