Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Метод Гомори для решения задачи целочисленного линейного программирования
Задачей целочисленноголинейного программирования (ЗЦЛП) называют ЗЛП, в которой на переменные налагается дополнительное ограничение – условие целочисленности. ЗЦЛП имеет вид:
где N1 – некоторое подмножество множества индексов N ={1,2, …,n}. Если N1=N, то задачу (1) – (4) называют полностью целочисленной, если N1¹N, - частично целочисленной. Метод Гомориявляется одним из методов решения задач целочисленного линейного программирования. Идея метода Гомори решения задачи (1) – (4) заключается в следующем. Отбрасывается условие целочисленности (4), и полученная ЗЛП (1) – (3) решается симплекс-методом. Если оптимальное решение задачи (1) – (3) удовлетворяет ограничению (4), т.е. является целочисленным, то оно является и решением исходной задачи (1) – (4). Если оптимальное решение задачи (1) – (3) не удовлетворяет ограничению (4), то к основным ограничениям (2) добавляется новое линейное ограничение, обладающее следующими свойствами: 1) оптимальный нецелочисленный план задачи (1) – (3) ему не удовлетворяет; 2) любой целочисленный план задачи (1) – (3) ему удовлетворяет. Затем решается расширенная задача. Процесс повторяется до получения целочисленного решения. Способы построения дополнительного линейного ограничения различны для полностью и частично целочисленных ЗЛП. В силу свойств 1 и 2 дополнительное ограничение называют еще отсечением Гомори, а метод Гомори – методом отсечения. Рассмотрим метод Гомори для решения полностью целочисленных ЗЛП. Пусть задача (1) – (3) решена симплекс-методом, х0 – ее оптимальный план, а табл. 7.1 - оптимальная симплексная таблица.  Таблица 6.1
Если все значения х0ip
Дополнительное линейное ограничение, или отсечение Гомори, будет иметь вид
В ограничение (5) вводим дополнительную переменную
где xn+1³0. Равенство (6) умножим на -1 и получим
Припишем ограничение (7) к симплексной таблице 1. При том переменная xn+1 будет базисной. Получим расширенную таблицу 2. Расширенную задачу решают начиная с табл.6.2. Так как в столбце свободных членов табл.6.2 есть отрицательное число, для решения расширенной задачи выполняют следующие операции.
Таблица 6.2
1. Просматривают строку, содержащую отрицательное число в столбце свободных членов, и выбирают любое отрицательное число в этой строке. Выбранное число определяет разрешающий столбец. 2. Для чисел с одинаковыми знаками составляют симплексные отношения. 3. Наименьшее симплексное отношение определяет разрешающую строку. На пересечении разрешающей строки и разрешающего столбца находится разрешающий элемент. 4. С найденным разрешающим элементом выполняют симплексные преобразования. Пример. Предприятие производит две модели А и В сборных книжных полок. Их производство ограничено наличием сырья (высококачественных досок) и временем машинной обработки. Для каждого изделия модели А требуется 2 м2 досок, а для изделия В – 5 м2. Малое предприятие может получить от своих поставщиков до 1600 м2 досок в неделю. Для изготовления каждого изделия модели А требуется 10 мин машинной обработки, а изделие модели В – 12 мин. Время машинной обработки в неделю 100 ч. Сколько изделий каждой модели следует выпускать малому предприятию в неделю для получения максимальной прибыли, если каждое изделие модели А приносит 20 ден. ед. прибыли, а каждое изделие модели В – 40 ден. ед.? Решение Математическая модель задачи имеет вид
x1, x2 – целые. Преобразуем задачу, умножив обе части второго неравенства на 30. Получим задачу
x1, x2 – целые.
По методу Гомори для определения оптимального плана задачи ,решим ЗЛП симплекс-методом. Приведем ее к каноническому виду:
В процессе решения задачи получаются следующие симплекс таблицы Таблица 6.3
Таблица 6. 4
Таблица 6.5
Табл.6.5 – оптимальная симплексная таблица, x0=(x01;x02), где x01=
Так как
ограничение (*) примет вид
Введем в ограничение дополнительную переменную
Домножим ограничение на -1:
Припишем ограничение к табл.7.5 и получим табл.7.6
Таблица 7.6
Следуя методу Гомори, выполним симплексные преобразования табл.6.6 с разрешающим элементом -11/13. Получим табл.6.7.
Таблица 6.7
Имеем оптимальный целочисленный план расширенной задачи. Тогда оптимальный план исходной задачи х0=(415;154). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 404. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 (1)
(1) (2)
(2) (3)
(3)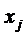 - целые числа;
- целые числа;  (4)
(4) - целые, то х0 – решение задачи (1) – (4). Пусть среди чисел х0ip
- целые, то х0 – решение задачи (1) – (4). Пусть среди чисел х0ip 
 (5)
(5) 
 (6)
(6) (7)
(7)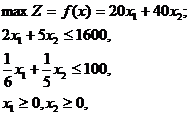

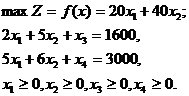



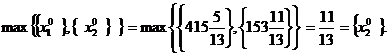 По первой строке табл.7.5 строим дополнительное линейное ограничение:
По первой строке табл.7.5 строим дополнительное линейное ограничение: (*)
(*)