
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Дополнительные условия в транспортных задачах.
В практике обычно при составлении экономико-математической модели задачи транспортного типа приходится вводить целый ряд дополнительных ограничений, вследствие чего поиск оптимального решения усложняется. Рассмотрим наиболее часто встречающиеся случаи. Нередко целесообразно минимизировать суммарные затраты на производство и транспортировку продукции. С подобной задачей можно столкнуться при решении вопросов, связанных с оптимальным размещением производственных объектов. Здесь может оказаться экономически более выгодным доставлять сырье из отдаленного источника, но зато при меньшей его себестоимости. В таких задачах критерием оптимальности служит сумма затрат на производство единицы груза и на его перевозку. Часто необходимо вводить ограничения, согласно которым, отдельные поставки от определенного поставщика определенному потребителю должны быть исключены (из- за отсутствия достаточного количества транспорта или необходимых условий хранения груза, чрезмерной перегрузки коммуникаций и т. п.). Значит, в матрице перевозок, содержащей оптимальный план, определенные клетки должны остаться свободными. Это достигается искусственным завышением показателей cij в клетках, перевозки через которые следует запретить, до значений, заведомо больших всех, с которыми их придется сравнивать в процессе решения задачи. Иногда приходится учитывать ограничения по пропускной способности некоторых маршрутов. Если, например, по маршруту i-jможно провезти не более d единиц груза, то j-й столбец матрицы перевозок разбивается на два: j’и j’’. В первом спрос принимается равным разности между действительным спросом bjи ограничением d, во втором — равным ограничению d. Тарифы cij в обоих столбцах одинаковы и равны данным, но в первом в клетке, соответствующей ограничению, вместо истинного тарифа cks ставится искусственно завышенный тариф М (клетка блокируется). Затем задача решается обычным способом.  Может случиться, что некоторые поставки по определенным маршрутам обязательны и должны войти в оптимальный план независимо от того, выгодно это или нет в условиях всей задачи. Тогда соответственно уменьшают запасы груза у поставщиков и спрос у потребителей и решают задачу относительно тех поставок, которые не обязательны. Во многих задачах транспортного типа целевая функция максимизируется. Поэтому при составлении начального опорного плана в первую очередь стараются заполнять клетки, с наиболее высокими значениями показателя критерия оптимальности. Выбор клетки, подлежащей заполнению при переходе от одного опорного плана к другому, должен производиться не по отрицательной, а по положительной оценке. Оптимальным будет опорный план, которому в распределительной таблице сопутствуют свободные клетки с неположительными оценками (все sij £ 0). Пример.На четырех ткацких станках с объемом рабочего времени 200, 300, 250 и 400 станко ч за 1ч можно изготовить соответственно 260, 200, 340 и 500м ткани трех артикулов I, II, III. Составить оптимальную программу загрузки станков, если прибыль (в ден. ед.) от реализации 1м ткани i-го артикула при ее изготовлении на j-м станке характеризуется элементами матрицы
а суммарная потребность в ткани каждого из артикулов равна 200, 100 и 150 тыс. м, учитывая, что ткань I артикула не может производиться на третьем станке. РешениеТребуется установить, какое количество ткани каждого артикула должно изготавливаться на каждом станке, чтобы общая прибыль от реализации готовой продукции была максимальной. На первом станке можно изготовить 260 × 200 = 52 тыс. м ткани, на втором – 60, на третьем – 85, на четвертом – 200, а всего – 397 тыс. м. Поскольку суммарная потребность в ткани всех трех артикулов составляет 450 тыс. м, то на 53 тыс. м спрос удовлетворить не удастся. Составить математическую модель задачи. Обозначим через xij количество ткани (в тыс. м) i-го артикула, изготовленной на j-м станке, а через f(x11,…,x34) – общую прибыль, тогда решение задачи сведется к максимизации функции
f = 2,5x11 + …+ 0,9x34 (7) при ограничениях:
Коэффициенты функции (7) характеризуют прибыль (в тыс. ден. ед.) от реализации каждой тысячи метров ткани; неравенства (9) – о полном использовании производственных мощностей. Из соотношений (8) – (10) видно, что рассматриваемая задача относится к задачам транспортного типа и имеет открытую модель. «Поставками» в данном случае мы считаем объем выпуска ткани, а «тарифами» - прибыль от реализации каждой тысячи метров ткани каждого из артикулов. Для преобразования модели (7) – (10) в закрытую следует ввести в рассмотрение фиктивный пятый станок, который позволит «выпустить» недостающие для удовлетворения спроса 53 тыс. м ткани. «Прибыль» от реализации ткани, «выпускаемой» фиктивным станком, естественно положить равной нулю. Преобразованная модель примет следующий вид:
где В табл. 5.5 содержится начальный опорный план загрузки станков. При его составлении станки загружались в первую очередь изготовлением тканей наиболее прибыльных артикулов. За очередностью заполнения клеток таблицы можно проследить по индексам, которыми снабжены величины xij. По условию задачи на третьем станке ткань I артикула изготавливать нельзя. В связи с этим клетку (1;3) в табл.1 пришлось заблокировать, приписав ей показатель М, равный очень большому по абсолютной величине отрицательному числу («отрицательная» прибыль!). С практической точки зрения это можно истолковать таким образом, что загрузка клетки (1;3) причинила бы производству очень большой ущерб. Поскольку всегда êМ ê> êu1+v3 ê, то при любом плане загрузки станков оценка клетки (1;3) Dks = M – (u1+v3) будет отрицательна, а поэтому клетка останется незанятой, что и требуется. Таблица 5.5
Для исследования плана на оптимальность вычисление потенциалов в табл.1 начато с u3 = 0. То, что свободные клетки (3;1) и (3;4) имеют положительные оценки, говорит о неоптимальности плана. Заполнение клетки (3;1) числом
Таблица 5.6
Итак, все 200 тыс. м ткани I артикула следует изготавливать на четвертом станке, на что потребуется 200 : 0,5 = 400 станко-часов; ткань II артикула – на первом (15 тыс. м) и третьем (85 тыс. м) станках, для чего потребуется соответственно 15 : 0,26 = 57,69 и 85 : 0,34 = 250 станко-часов; ткань III артикула – на первом (37 тыс. м) и втором (60 тыс. м) станках, и на это потребуется соответственно 37 : 0,26 = 142,31 и 60 : 0,2 = 300 станко-часов. Общая прибыль составит 835,1 тыс. ден. ед. Неудовлетворенным останется спрос на 53 тыс. м ткани III артикула. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 527. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 (8)
(8)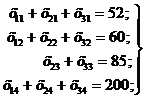 (9)
(9) (10)
(10)
 ,
,  ,
,  - «выпуск» ткани I, II, III артикула пятым станком.
- «выпуск» ткани I, II, III артикула пятым станком. способствовало увеличению прибыли при новом плане (табл.5.6) на 0,5 × 37 = 18,5 тыс. ден. ед. Новый план оказался оптимальным, так как оценки всех свободных клеток отрицательные.
способствовало увеличению прибыли при новом плане (табл.5.6) на 0,5 × 37 = 18,5 тыс. ден. ед. Новый план оказался оптимальным, так как оценки всех свободных клеток отрицательные.