
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Анализ решения задач линейного программированияВ математическом программировании доказывается следующая теорема двойственности (теорема об оценках). Теорема 1.В оптимальном решении двойственной задачи значения переменных yi*(оценок) численно равны частным производным ¶ fmax /¶ bi для исходной задачи. Отсюда при малых изменениях Dbi свободных членов bi следует приближенное равенство
Некоторые аспекты применения двойственных оценок оптимального плана для его экономико-математического анализа рассмотрим на примере задачи рационального использования ресурсов по критерию максимума прибыли. В матрично-векторной форме задача записывается следующим образом:
где Анализ задач линейного программирования может проводиться путем сопоставления различных вариантов решений; с помощью анализа внутренней структуры каждого из полученных решений, базирующегося на свойствах двойственных оценок, приведенных ниже. Двойственные оценки являются: 1) показателем дефицитности ресурсов и продукции. Это их свойство следует из теоремы. Величина yi* является оценкой i-го ресурса. Чем больше значение оценки yi*, тем выше дефицитность ресурса. Для недефицитного ресурса yi* = 0; 2) показателем влияния ограничений на значение целевой функции. Ранее было отмечено, что yi* = ¶ fmax /¶ bi. При незначительном приращении Dbi является точной мерой влияния ограничений на целевую функцию. Поэтому представляет интерес определение предельных значений ограничений (нижней и верхней границ), в которых величины оценок остаются неизменными;  3) показателем эффективности производства отдельных видов продукции с позиции критерия оптимальности. Это свойство следует из теоремы. Его суть заключается в том, что в оптимальный план может быть включена лишь та продукция j-го вида, для которой выполняется условие
4) инструментом сопоставления суммарных условных затрат и результатов. Это свойство следует из принципа двойственности, в котором устанавливается связь между значениями функций прямой и двойственной задач. Из ранее данной экономической интерпретации двойственных задач следует, что равенство значений целевых функций при оптимальных планах означает, что оценка всех затрат производства должна равняться оценке производственного продукта. Для целей анализа большое значение имеет матрица А-1 = [dij], обратная матрице базиса оптимального плана A = [аij]. Двойственные оценки можно использовать для экономического анализа решения при условии, что ограничения на ресурсы изменяются лишь в определенных пределах. В этой связи говорят о допустимом интервале устойчивости оценок. Интервал устойчивости оценок по отношению к i-му ограничению имеет вид
где
Целесообразность включения в план новых видов продукции оценивается характеристикой
Если Пусть имеется возможность приобрести дополнительно i-й ресурс в объеме
Пример. Для изготовления четырех видов продукции (А, Б, В и Г) используются три вида ресурсов (I, II, III). Наличие ресурсов, нормы их расхода на единицу продукции и получаемая прибыль от единицы продукции заданы в табл. Необходимо: а) найти оптимальные решения прямой и двойственной задач; б) определить изменение максимальной прибыли при изменении ресурсов: I вида – на -10ед., II – на +60, III – на +30 ед.; оценить раздельное и суммарное влияние этих изменений на величину максимальной прибыли; в) оценить целесообразность введения в план пятого вида продукции Д, нормы затрат ресурсов на единицу которого равны соответственно 2, 4, 2, а прибыль – 15; г) оценить целесообразность закупки 100 ед. ресурса III вида по цене c3 = 0,5. Таблица 4.5
Решение Математическая модель задачи имеет вид:
а)Решаем задачу симплекс-методом (опуская подробности, приведем сразу оптимальное решение в табл.4.6).
Таблица 4.6
Значения целевой функции и неизвестных величин оптимального плана следующие: f* = 480, х1* = 60, х2* = 120, х3* = 0, х4* = х5* = х6* = х7* = 0. Базисными неизвестными, входящими в оптимальный план, являются х1, х2 и х3. Выпишем матрицу из коэффициентов при базисных неизвестных:
Из табл. выпишем матрицу, обратную матрице А,
Используя соответствие между переменными исходной и двойственной задач, запишем оптимальное решение двойственной задачи: y1* = 8/5, y2* = 3/5, y3* = 1/5, y4* = y5* = y6* = 0, y7* = 2/5, f(y)min= 480. Как показывают значения оценок, наиболее дефицитным является ресурс I, так как y1* = 8/5, а наименее дефицитным – ресурс III, так как y3* = 1/5. Чтобы определить изменение максимальной прибыли при изменении ресурсов, необходимо найти интервалы устойчивости двойственных оценок, в пределах которых они точно измеряют влияние ограничений на целевую функцию. Определим интервал устойчивости оценок по отношению к ограничению по ресурсу I вида. Используя формулы находим:
В соответствии с формулами интервал устойчивости оценок по отношению к первому ограничению принимает следующий вид:
Аналогичным образом находим интервалы устойчивости оценок по отношению к ограничениям по двум другим видам ресурсов: по ресурсу II - [60;360], по ресурсу III - [300;450]. б) Так как изменения ресурсов находятся в пределах устойчивости оценок, то их раздельное влияние на величину прибыли
Суммарное влияние
в) Оценим целесообразность введения в план пятого вида продукции (Д). Для этого по формуле вычислим характеристику:
Так как прибыль превышает затраты, введение в план пятого вида продукции выгодно. г) Приращение третьего ресурса на величину
Транспортная задача Постановка транспортной задачи в матричной форме. Построение исходного опорного плана Транспортная задача является специальным типом задач ЛП. Экономическая постановка этой задачи следующая. В m пунктах отправления A1, …, Am сосредоточен однородный груз в количествах соответственно а1, …, аm единиц. Имеющийся груз необходимо доставить потребителям В1, …, Вn, спрос которых выражается величинами b1, …, bn единиц. Известна стоимость сij перевозки единицы груза из i-го (i = l, m) пункта отправления в j-й (j = 1, n) пункт назначения. Требуется составить план перевозок, который полностью удовлетворяет спрос потребителей в грузе, и при этом суммарные транспортные издержки минимизируются. Для построения экономико-математической модели транспортной задачи рассмотрим матрицу
где xij (i = 1, m; j = 1, n) обозначает количество единиц груза, которое необходимо доставить из i-гo пункта отправления в j-й пункт назначения. Матрицу X = [xij]m×n будем называть матрицей перевозок. Предполагается, что все xij ≥ 0. Удельные транспортные издержки (расходы) запишем в форме матрицы С = [сij]m×n и назовем ее матрицей тарифов. Для наглядности условия транспортной задачи можно представить таблицей (табл.5.1), которую будем называть распределительной. Распределительную таблицу называют иногда табличной или матричной моделью транспортной задачи. Таблица 5.1
Экономико-математическая модель транспортной задачи должна отражать все условия и цель задачи в математической форме. Так, переменные xij (i = 1, m; j = 1, n) должны удовлетворять ограничениям по запасам, потребностям и условиям неотрицательности. В математической форме эти условия можно записать так:
Цель транспортной задачи — минимизировать общие затраты на реализацию плана перевозок, которые можно представить функцией
Итак, математически транспортная задача ставится так: Даны система ограничений (1) при условии (2) и линейная функция (3). Требуется среди множества решений системы (1) найти такое неотрицательное решение, при котором линейная функция (3) принимает минимальное значение (минимизируется). [2, с. 144-145] Будем называть план перевозок X = [xij]m×n допустимым, если он удовлетворяет ограничениям (1) и (2). Допустимый план перевозок, доставляющий минимум целевой функции (3), называется оптимальным. Теорема 1 (о существовании допустимого плана). Для того чтобы транспортная задача имела допустимые планы, необходимо и достаточно выполнение равенства
Доказательство. Просуммировав в распределительной табл. 1 элементы xij раздельно по индексам i и j, получим: Очевидно, что суммируются все элементы xij как по строкам, так и по столбцам, различие лишь в перестановке этих элементов. Однако от перестановки слагаемых сумма не меняется. Поэтому равенство
является необходимым условием разрешимости транспортной задачи. Для доказательства достаточности условия (4) покажем, что если это условие выполняется, то всегда имеется допустимый план. Обозначим
Переменные xij выразим через данные задачи следующим образом:
Поскольку аi ≥ 0 и bj ≥ 0, то и А > 0, а поэтому и xij ≥ (i = l, m; j=1,n). Покажем, что переменные (5) составляют допустимый план. Этот набор неотрицательных чисел будет составлять допустимый план тогда, когда он удовлетворяет системе ограничений (1). Просуммируем равенства (5) по индексу i. Получим
Поскольку индекс j не зависит от индекса i, в равенстве (6) вынесем bj/A за знак суммы и получим
Аналогично, суммируя равенства (5) по индексу j, получаем:
Следовательно, набор чисел xij = aibj/A удовлетворяет системе ограничений задачи, а потому является допустимым планом. [2, с. 146] Модель транспортной задачи называют закрытой, если суммарный объем груза, имеющегося у поставщиков, равен суммарному спросу потребителей, т. е. выполняется равенство:
Если для транспортной задачи выполняется одно из условий:
то модель задачи называют открытой. Для разрешимости транспортной задачи с открытой моделью необходимо преобразовать ее в закрытую. Так, при выполнении первого условия необходимо ввести фиктивный (n + 1)-й пункт назначения Вn+1, т. е. в матрице задачи предусматривается дополнительный столбец. Спрос фиктивного потребителя полагают равным небалансу, т. е.
а все тарифы — одинаковыми, чаще всего равными нулю, т. е. ci, n+1 = 0 (i=l, m). Аналогично при выполнении второго условия вводится фиктивный поставщик Аm + 1, запас груза у которого равен
а тарифы дополнительной строки распределительной таблицы равны нулю, т. е. cm + 1, j = 0 (j=1, n). При преобразовании открытой задачи в закрытую целевая функция не меняется, так как все слагаемые, соответствующие дополнительным перевозкам, равны нулю. Теорема 2 (о ранге матрицы). Ранг матрицы А транспортной задачи на единицу меньше числа уравнений: r(A) = m + n - 1. Доказательство. Матрица системы ограничений (1) имеет вид
В каждом столбце матрицы А содержатся только два элемента, равных единице, остальные элементы равны нулю. При этом, если сложить первые m строк матрицы, получим строку, элементы которой будут единицы. Этот же результат получаем, если сложить последние n строк. Обозначая i-ю строку через рi получаем: pl + p2 + ... + pm = pm+1 + pm+2 + ... + pm + n. Отсюда видно, что любая строка есть линейная комбинация остальных строк. Значит, не меняя ранга матрицы А, можно вычеркнуть, например, последнюю строку. Минор (m + n - 1)-го порядка получившейся матрицы, составленный из столбцов коэффициентов при x1n, х2n, …, xmn, x11, x12, …, x1, n-1 будет отличен от нуля, что и доказывает теорему. Построение опорных планов будем производить непосредственно в распределительной таблице. Если в плане перевозок переменная хik равна некоторому числу а ≠ 0, то это число записываем в соответствующую клетку (i; k) и считаем ее занятой или базисной, если же xik = 0, то клетку (i, k) оставляем свободной. При этом число занятых опорным планом клеток в соответствии с теоремой 2 должно быть равно m + n - 1, а остальные mn - (m + n - 1) = (m - 1)(n - 1) клеток будут свободными. Рассмотрим правило «северо-западного угла». Сущность его состоит в следующем. Пользуясь табл. 1, будем распределять груз, начиная с загрузки левой верхней, условно называемой северо-западной, клетки (1; 1), двигаясь затем от нее по строке вправо или по столбцу вниз. В клетку (1; 1) занесем меньшее из чисел а1, b1, т. е. x11 = min (a1, b1). Если а1 > b1, то x11 = b1 и первый потребитель В1 будет полностью удовлетворен. В дальнейшем 1-й столбец таблицы в расчет не принимается; в нем переменные хi1 = 0 для i = 2, m. Двигаясь вправо по первой строке таблицы, заносим в соседнюю клетку (1; 2) меньшее из чисел (a1 – b1) и b2, т. е. x12 = min (а1 – b1, b2). Если (а1 – b1) < b2, то запасы первого поставщика исчерпаны и первая строка таблицы в дальнейшем в расчет не принимается. Переходим к аналогичному распределению запаса груза второго поставщика. Если b1 > a1, то x11 = min (a1, b1) = а1. При этом запас первого поставщика будет исчерпан, а потому x1k = 0 для k = 2, n. Первая строка из дальнейшего рассмотрения исключается. Переходим к распределению запасов второго поставщика. В клетку (2; 1) заносим наименьшее из чисел (а2, b1 – а1). Заполнив таким образом клетку (1; 2) или (2; 1), переходим к загрузке следующей клетки по второй строке либо по второму столбцу. Процесс распределения по второй, третьей и последующим строкам (столбцам) производится аналогично распределению по первой строке или первому столбцу до тех пор, пока не исчерпаются ресурсы. Последней заполняется клетка (m; n). Рассмотрим правило «минимального элемента». Сущность его состоит в следующем. Просматриваются тарифы табл. 1 и в первую очередь заполняется клетка с минимальным значением тарифа. При этом в клетку записывается максимально возможное значение поставки. Затем из рассмотрения исключают строку, соответствующую поставщику, запасы которого полностью израсходованы, или столбец, соответствующий потребителю, спрос которого полностью удовлетворен. После этого из оставшихся клеток таблицы снова выбирают клетку с наименьшим тарифом. Процесс распределения заканчивается, когда все запасы поставщиков исчерпаны, а спрос потребителей полностью удовлетворен. В результате получаем опорный план, который должен содержать m + n - 1 загруженных клеток. В процессе заполнения таблицы могут быть одновременно исключены строка и столбец. Так бывает, когда полностью исчерпывается запас груза и полностью удовлетворяется спрос (вырожденная задача). В этом случае в свободные клетки надо записать число 0 — «нуль-загрузка», условно считая такую клетку занятой. Однако число 0 записывается в те свободные клетки, которые не образуют циклов с ранее занятыми клетками. Рассмотрим метод Фогеля. Сущность его состоит в следующем. В табл. 1 по строкам и столбцам определяется разность между двумя наименьшими тарифами. Отмечается наибольшая разность знаком □. Далее в строке (столбце) с наибольшей разностью заполняется клетка с наименьшим тарифом. Строки (столбцы) с нулевым остатком груза в дальнейшем в расчет не принимаются. На каждом этапе загружается только одна клетка. Распределение груза производится, как и по выше рассмотренным правилам. Среди полученных опорных планов Х1 Х2, Х3 с различными значениями целевой функции лучшим является Х3. Будет ли он оптимальным? Чтобы ответить на этот вопрос, необходимо знать признак оптимальности. Метод потенциалов Теорема 3. Если план X* = [хij*]m×n транспортной задачи является оптимальным, то ему соответствует система из m + n чисел ui*, vj*, удовлетворяющих условиям ui* + vj* = cij для хij* >0 и ui* + vj* ≤ cij для хij* = 0 (i=1 , m; j = 1, n) Числа ui* и vj*, называются потенциалами соответственно i-го поставщика и j-го потребителя. Доказательство. Транспортную задачу (1) - (3) можно рассматривать как двойственную задачу к некоторой исходной задаче, решаемой на максимум. Построим эту задачу. Так, если i-му ограничению двойственной задачи хi1 + хi2 + ... + xin = ai в исходной задаче соответствует переменная ui (i = l, m), а j-му ограничению х1j + х2j + ... + xmj = bi — переменная vj (j = 1, n), то исходной будет задача: найти максимальное значение функции
при ограничениях ui + vj ≤ cij (i=1, m; j = 1, n). Оптимальным для двойственной задачи является план х*, а для исходной у* = (ui*; vj*). Для пары взаимодвойственных задач на основании первой теоремы двойственности имеет место равенство ƒmin = ƒmax, а по второй теореме двойственности выполняются условия ui* + vj* = cij для хij*>0, ui* + vj* ≤ cij для хij* = 0 (i=l, m; j=l , n). Из теоремы следует, что для оптимального плана транспортной задачи необходимо выполнение условий: 1) каждой занятой клетке в распределительной таблице соответствует сумма потенциалов, равная тарифу этой клетки, т. е. ui + vj = cij; 2) каждой свободной клетке соответствует сумма потенциалов, не превышающая тарифа этой клетки, т. е. ui + vj ≤ cij. Доказанная теорема носит название теоремы о потенциалах. На ней основан специальный метод решения транспортной задачи, названный методом потенциалов. В соответствии с введенным понятием потенциалов и с учетом связей между моделями двойственных задач каждому поставщику (ограничению по запасам) поставим в соответствие потенциал ui, (i = l, m), а каждому потребителю (ограничению по спросу) — потенциал vj, (j = 1, n). Согласно теореме о потенциалах, каждой занятой клетке будет соответствовать уравнение ui + vj = сij;. Так как всех занятых клеток должно быть m + n - 1, т. е. на единицу меньше числа потенциалов, то для определения чисел ui, vj, необходимо решить систему из m + n - 1 уравнений ui + vj = сij с m + n неизвестными. Система неопределенная, и, чтобы найти частные решения, одному из потенциалов придаем произвольное числовое значение, тогда остальные потенциалы определяются однозначно. Для облегчения расчетов одному из потенциалов придают обычно значение, равное нулю. Для исследования плана на оптимальность для каждой свободной клетки проверяется условие ui + vj ≤ сij. Если хотя бы одна свободная клетка не удовлетворяет данному условию, то опорный план не является оптимальным, его можно улучшить за счет загрузки этой клетки. Если таких клеток несколько, то наиболее перспективной для загрузки является клетка, для которой разность (оценка) между тарифом клетки и суммой потенциалов наименьшая, т. е. sij = сij - (ui + vj) < 0. Если для всех свободных клеток оценки sij ≥ 0, то опорный план перевозок является оптимальным. Итак, если для опорного плана перевозок указанное условие оптимальности не выполняется, то за счет загрузки свободной клетки с отрицательной оценкой план перевозок улучшается. Для наиболее перспективной свободной клетки строится замкнутый цикл с вершинами в загруженных клетках. Вершинам этого цикла условно приписываются знаки: свободной клетке - плюс, следующей по часовой или против часовой стрелки занятой клетке - минус, следующей - снова плюс и т. д. Из поставок в клетках цикла с «отрицательными» вершинами выбирается наименьшее количество λ груза, которое и перемещается по клеткам этого цикла: прибавляется к поставкам в положительных вершинах и вычитается из поставок в отрицательных вершинах, в результате чего баланс цикла не нарушится (рис.6. 1). В общем случае цикл представляет собой замкнутую ломаную линию, состоящую из звеньев, пересекающихся под прямым углом. Каждое звено соединяет две клетки строки (столбца). Цикл включает одну свободную клетку, остальные клетки цикла заняты. В цикле всегда четное число клеток. Для свободной клетки всегда можно построить единственный цикл. Если из занятых клеток образуется цикл, то план перевозок не является опорным. Цикл строится лишь для свободной клетки.
Рис.5. 1. Сформулируем алгоритм решения транспортной задачи методом потенциалов: 1)построить опорный план по одному из правил, 2)вычислить потенциалы поставщиков и потребителей ui и vj (i = 1, m, j = 1, n), решив систему уравнений вида ui + vj = сij; 3) вычислить оценки sij для всех свободных клеток по формуле sij = сij - (ui + vj). Если все sij ≥ 0, то полученный план является оптимальным. При этом если все sij >0, то полученный оптимальный план единственный. В случае, если хотя бы одна оценка sij = 0, имеем бесчисленное множество оптимальных планов с одним и тем же значением целевой функции. Пример. Найти оптимальный план перевозок ТЗ, условие которой представлено в табл.5.2. Таблица 5. 2
РешениеПоскольку запасы грузов превышают спрос потребителей, вводится фиктивный потребитель, спрос которого
Все тарифы фиктивного потребителя равны нулю: Исходное опорное решение получим, например, по правилу «минимального элемента» табл.5.3. Таблица 5.3
Получен невырожденный план. Потенциалы поставщиков и потребителей определены непосредственно в таблице. Оценки свободных клеток следующие: s12 = 10 – 5 = 5, s13 = 5 – 0 = 5, s15 = 0 + 2 = 2, s22 = 7 – (2 + 5) = 0, s24 = 8 – (2 + 3) = 3, s33 = 12 – 4 = 8, s34 = 11 – (4 + 3) = 4, s35 = 0 – (4 - 2) = -2. Среди оценок имеется отрицательная (s35 = -2). План перевозок можно улучшить за счет загрузки клетки (3;5). В отрицательных вершинах построенного для клетки (3;5) цикла наименьшее количество груза равно min (10,15) = 10 ед. После смещения по циклу 10 ед. груза получим новый план перевозок (табл.5.4). Как и для предыдущего плана перевозок, все потенциалы поставщиков и потребителей определены в таблице. Оценки свободных клеток: s12 = 10 – 5 = 5, s13 = 5 – 0 = 5, s15 = 0 – (0 - 4) = 4, s22 = 7 – (2 + 5) = 0, s24 = 8 – (2 + 3) = 3, s25 = 0 – (2 – 4) = 2, s33 = 12 – 4 = 8, s34 = 11 – (4 + 3) = 4. Оценки всех свободных клеток положительны, полученный план перевозок является оптимальным:
со значением целевой функции f(X*) = 1050 ден. ед. Таблица 5.4
Загрузка x35 = 10 т для фиктивного потребителя указывает на остаток нераспределенного груза 10 т у поставщика А3.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 489. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
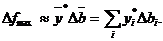

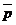 - вектор прибыли продукции;
- вектор прибыли продукции;  - искомый вектор – план производства продукции; А- матрица коэффициентов при неизвестных – нормы потребления ресурсов;
- искомый вектор – план производства продукции; А- матрица коэффициентов при неизвестных – нормы потребления ресурсов;  - вектор ограничений по ресурсам;
- вектор ограничений по ресурсам;  - вектор оценок ресурсов.
- вектор оценок ресурсов.

 называют нижним пределом уменьшения, а
называют нижним пределом уменьшения, а 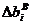 - верхним пределом увеличения и вычисляют по формулам:
- верхним пределом увеличения и вычисляют по формулам:

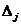 < 0, то данный вид продукции после введения в план улучшает его. При
< 0, то данный вид продукции после введения в план улучшает его. При  . Эта величина находится в пределах устойчивости двойственных оценок. Цена единицы ресурса равна ci. Следовательно, приращение прибыли
. Эта величина находится в пределах устойчивости двойственных оценок. Цена единицы ресурса равна ci. Следовательно, приращение прибыли 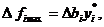 в то время как затраты на приобретение ресурса составляют
в то время как затраты на приобретение ресурса составляют 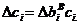 Данное мероприятие будет эффективным, если обеспечит дополнительную прибыль, т. е. если
Данное мероприятие будет эффективным, если обеспечит дополнительную прибыль, т. е. если  > 0, где
> 0, где





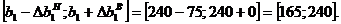
 определяется произведением оценки
определяется произведением оценки 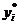 и величины изменения
и величины изменения 

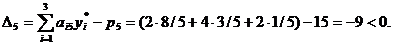
 находится в пределах устойчивости двойственных оценок. Следовательно,
находится в пределах устойчивости двойственных оценок. Следовательно, 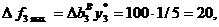 в то время как затраты на приобретение 100 ед. ресурса III вида
в то время как затраты на приобретение 100 ед. ресурса III вида  Поскольку величина Dp дополнительной прибыли отрицательна (Dp3 = Df3 - Dc3 = 20 - 50 = -30), закупать ресурс III вида нецелесообразно.
Поскольку величина Dp дополнительной прибыли отрицательна (Dp3 = Df3 - Dc3 = 20 - 50 = -30), закупать ресурс III вида нецелесообразно.
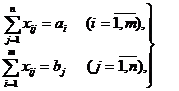 (1)
(1) (2)
(2) (3)
(3)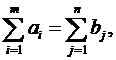 (4)
(4)

 (5)
(5)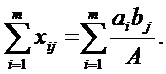 (6)
(6)
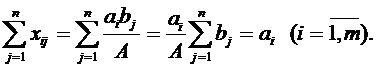

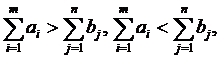
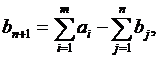
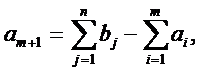

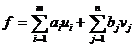

 т.
т.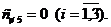 Имеем ТЗ закрытого типа, которую решаем методом потенциалов.
Имеем ТЗ закрытого типа, которую решаем методом потенциалов. 20
20

 6
6