
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Найти: а) параметр с; б) моду; в) медиану.4 a). Используя свойство (5) плотности распределения, получим: Плотность распределения имеет вид: б) МодаMo СВ Х – это точка максимума функции в) Медиана Мe определяется из уравнения Следовательно, Математическое ожидание характеризует среднее значение СВ и обозначается М[X] или mx.Под символом М[X] понимают оператор математического ожидания, примененный к СВ Х. Оператор имеет различные выражения для дискретной и непрерывной СВ Х. Математическое ожидание дискретной СВ Х есть сумма произведений всех возможных значений СВ на вероятности принятия этих значений. М[X]= Математическое ожидание непрерывной СВ X есть интеграл: М[Х] = Свойства математического ожидания 1. М[С]=С 2. М[CX]=CМ[X] 3. М[X1+X2+...+Xn]= M[X1]+ M[X2]+...+ M[Xn] 4. Для независимых случайных величин X1,×X2,×...×,Xn: М[X1×X2×...×Xn]= M[X1]× M[X2]×...× M[Xn]. Пример 4.5. Изделия испытываются на надежность. Вероятность выхода из строя за время испытания для каждого изделия равна р. Испытания заканчиваются после первого же вышедшего из строя изделия. Найти математическое ожидание СВ Х- числа проверенных изделий. 4Если X- случайное число проверенных изделий, то ряд распределения СВ Химеет вид:
гдеq=1-p. Математическое ожидание Х выражается суммой ряда:  М[Х]=1p+2pq+3pq2+...+kpqk-1 Легко заметить, что ряд, стоящий в скобках представляет собой результат дифференцирования геометрической прогрессии q+q2+q3+...+qk+...= Следовательно: М[Х]=р(1+2q+3q2+...+kqk-1+...)= Дисперсией Дисперсия характеризует рассеяние значений СВ вокруг ее математического ожидания. Символ D[X] означает оператор дисперсии, примененный к СВ Х. Свойства математического ожидания позволяют получить удобную формулу для определения дисперсии: D[X]=M[X2]-(M[X])2 (4.8) Дисперсия дискретной СВ Х вычисляют по формуле: D[X]= Или D[X]= Дисперсия непрерывной СВ Х вычисляют по формуле: D[X]= Или D[X]= Свойства дисперсии 1. D[C] = 0. 2. D[CX])=C2D[X]. 3. D[X1+X2+...+Xn ]= D[X1]+D[X2] +...+D[ Xn]. (Для независимых случайных величин X1,X2,...Xn). Из определения дисперсии следует, что она имеет размерность, равную квадрату размерности СВ. Чтобы избежать неудобств при характеристике СВ, наряду с дисперсией пользуются числовой характеристикой называемой средним квадратичным отклонением, имеющим такой же вероятностный смысл, как и дисперсия, а размерность совпадающую с размерностью Х. Средним квадратичным отклонением sх СВ Х называют квадратный корень из дисперсии:
sх = Теоретические моменты. Начальным теоретическим моментом k-го порядка Хk , т.е. Начальный момент k-го порядка дискретной СВ выражается суммой: непрерывной - интегралом:
Очевидно, что при k=1 Начальные моменты высших порядков используются главным образом для вычисления центральных моментов. Центральным моментомk-го порядка
Для дискретной СВХ центральный момент выражается суммой: для непрерывной - интегралом:
Центральный момент первого порядка Центральный момент любого порядка можно выразить через начальные моменты:
Асимметрией (коэффициентом асимметрии)
Коэффициент асимметрии характеризует “скошенность” графика плотности распределения вероятностей. Эксцессом она характеризует крутизну кривой распределения. Пример 4.7. Динамика курса доллара на биржевых торгах в течение 2-х месяцев 1999г. есть СВ Х, характеризующаяся плотностью распределения: 4График плотности распределения
Математическое ожидание По формуле Для определения центральных моментов воспользуемся формулами, выражающими центральные моменты через начальные:
Тогда:
Задачи 4.1. Для контроля качества продукции из партии готовых изделий делались случайные выборки и подсчитывались вероятности количества бракованных изделий. В результате получен ряд распределения СВ Х- количества бракованных изделий в партии (табл. а, б, в). Для каждого из рядов построить многоугольник распределения и функцию распределения, вычислить а)
б)
в)
Ответ: а) 4.2. СВ Х задана законом распределения:
Вычислить ее математическое ожидание, дисперсию и среднее квадратичное отклонение. Ответ: 4.3. Найти дисперсию и среднее квадратичное отклонение СВ Х, заданной законом распределения: а) б)
Ответ: а) 4.4. Реализатор выставляет на продажу 8 косметических наборов. Вероятность продажи одного косметического набора в день составляет 60%. Построить распределение вероятностей продажи наборов за день и ответить на следующие вопросы: 1) Сколько наборов в день в среднем продает реализатор? 2) Какова вероятность реализации за день не менее двух наборов? Ответ: 1) 4.8; 2) 4.5. Используя свойства математического ожидания, доказать, что математическое ожидание отклонения (Х-М[X])равнонулю. 4.6. Случайные величины Х и Y независимы. Найти дисперсию СВ Z = X + 4Y, если известно, что D(X) =3, D(Y) =2. Ответ: 35.
4.7. Найти математическое ожидание СВ Х, заданной законом распределения:
Ответ: 45. 4.8. Дан перечень возможных значений СВ X: x1=-1, x2=0, x3=1, а также известны математические ожидания этой и ее квадрата: M[X]=0,1, M[X2]=0,9. Найти закон распределения СВ Х.
4.9. СВ Х имеет возможные значения Х={‑2, 0, 3}. Известно, что математическое ожидание величины Х равно 1.0, а дисперсия равна 2.4. Найти закон распределения СВ Х.
4.10. Найти математическое ожидание и дисперсию величины Х- числа очков при одном бросании игральной кости и величины Y- суммы очков при бросании двух игральных костей. Ответ: 4.11. В лотерее разыгрывается кофеварка стоимостью 250 грн., миксер стоимостью 50 грн. и часы ценой 40 грн. Найти математическое ожидание выигрыша для лица, имеющего один билет, если общее число билетов равно 100. Ответ: 4.12. Производится два выстрела с вероятностями попадания в цель при каждом выстреле соответственно равными 0.6 и 0.7. Найти математическое ожидание общего числа попаданий. Ответ: 1,3. 4.13. СВ X имеет только два возможных значения: х1 и х2, причем х2 > x1. Вероятность того, что X примет значение x1 равна 0,1. Найти закон распределения величины X, если математическое ожидание и дисперсия известны: М(Х) = 3,9; D(X) = 0,09.
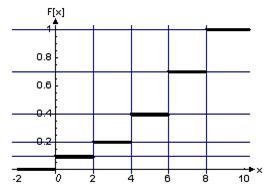
4.14. СВ Х задана рядом распределения:
Вычислить ее дисперсию и вероятность того, что Х не более 4 и не менее 2 Ответ: 4.15. СВ Х задана законом распределения:
Найти функцию распределения F(x), построить ее график и вычислить вероятность события (Х ≤ 4).
Р(Х ≤ 4) = 0.4.
4.16. СВ Х задана рядом распределения:
Найти функцию распределения F(x), построить ее график и вычислить вероятность события (-1Х Ответ:
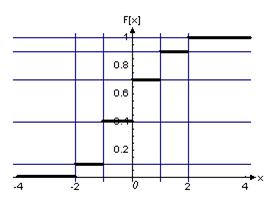
4.17. СВ Х задана рядом распределения:
Найти функцию распределения F(x), построить ее график и вычислить вероятность события (Х
Р(Х
4.18. Построить ряд распределения и функцию распределения числа
попаданий мячом в баскетбольную корзину при двух бросках, если вероятность попадания при одном броске равна 0.4.
4.19. Найти дисперсию СВ Х - числа появлений события А в двух независимых опытах, если вероятности появления события в этих опытах одинаковы и известно, что М[X]=0,9. Ответ: 0.495. 4.20. Дан перечень возможных значений CB Х={-2,0,3}. Известны также математическое ожидание, которое равно 1,0 и начальный момент второго порядка, который равен 5,0. Найти ряд распределения и вероятность того, что Х≥0.
; Р(Х ≥ 0) =
4.21. Найти математическое ожидание, моду, дисперсию и среднее квадратичное отклонение СВ Х, заданной законом распределения:
Ответ: 4.22. Найти математическое ожидание и дисперсию СВ Х, заданной функцией распределения: Ответ: 4.23. СВ Хзадана функцией распределения F(x). Построить график функции F(x) и найти вероятность того, что в результате опыта величина Хпримет значение, заключенное в интервале (a; b), если: а) б) в) г) Ответ:
4.24. Плотность распределения СВ Хзадана навсей числовой оси ОХ равенством Ответ: С= 1 / p. 4.25. Плотность распределения СВ задана с точность до параметра a. Найти значение a, если Ответ: а =0,5; Р(Х ≤ 3) =0,5. 4.26. Плотность вероятности СВ Х имеет вид Ответ: 4.27. Плотность распределения а) в) Ответ: а)
б)
в)
г)
4.28. Найти параметр с и математическое ожидание СВ Х, заданной функцией распределения: a) Ответ: а) 4.29. СВ Х задана плотностью распределения Ответ: 12,5. 4.30. Найти дисперсию СВ X, заданной функцией распределения:
4.31. СВ Х задана плотностью вероятности 4.32. Найти математическое ожидание, моду и медиану Х. Ответ: mx =0; Me =0; M0 - нет, т.к. график функции f(x) не имеет максимума. 4.33. СВ Х задана плотностью вероятности Ответ: M0(Х) = Me(Х) = 4. 4.34. СВ Х задана плотностью распределения: Ответ: 4.35. СВ Х задана функцией распределения Ответ: 4.36. Задана функция распределения СВ Х: Ответ: 0,117. 4.37. СВ Х задана функцией распределения Ответ: 4.38. СВ Х имеет плотность распределения вероятностей: Ответ: 4.39. СВ Х задана рядом распределения:
Вычислить ее математическое ожидание, дисперсию и асимметрию. Ответ: 4.40. Задана функция распределения СВ Ответ: 4.41. СВ Х имеет плотность распределения вероятностей:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 499. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 Þ
Þ  .
.
 , но
, но  =
= 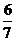 ¹0, следовательно данное распределение моды Mo не имеет.
¹0, следовательно данное распределение моды Mo не имеет. . Интегрируя и подставляя пределы интегрирования, получим:
. Интегрируя и подставляя пределы интегрирования, получим:  . Решая квадратное уравнение, находим корни
. Решая квадратное уравнение, находим корни  .
. . 3
. 3 =
=  (4.5)
(4.5) (4.6)
(4.6) +...= p(1+2q+3q2+...+kqk-1+...
+...= p(1+2q+3q2+...+kqk-1+... .
.
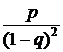 =
=  . 3
. 3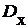 СВ Х называют математическое ожидание квадрата отклонения СВ от ее математического ожидания:
СВ Х называют математическое ожидание квадрата отклонения СВ от ее математического ожидания: = D[X]=M[(X-M[X])2] (4.7)
= D[X]=M[(X-M[X])2] (4.7)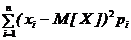 (4.9)
(4.9) ‑ (M[X])2 (4.10)
‑ (M[X])2 (4.10) (4.11)
(4.11) ‑(M[X]) 2 (4.12)
‑(M[X]) 2 (4.12) . (4.13)
. (4.13) СВ Х называют математическое ожидание величины
СВ Х называют математическое ожидание величины  (4.16)
(4.16) , (4.17)
, (4.17) (4.18)
(4.18) .
. СВ Х называют математическое ожидание величины
СВ Х называют математическое ожидание величины  :
: (4.19)
(4.19) , (4.20)
, (4.20)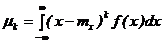 . (4.21)
. (4.21) , центральный момент второго порядка – это дисперсия:
, центральный момент второго порядка – это дисперсия:  .
.
 (4.22)
(4.22) ; и т.д.
; и т.д. распределения СВ Х называется величина:
распределения СВ Х называется величина: . (4.23)
. (4.23)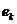 СВ Х называется величина
СВ Х называется величина , (4.24)
, (4.24)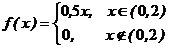 . Найти моду, медиану, асимметрию и эксцесс Х.
. Найти моду, медиану, асимметрию и эксцесс Х.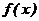 изображен на рис. 4.7. Мода М0этого распределения отсутствует, т.к.
изображен на рис. 4.7. Мода М0этого распределения отсутствует, т.к.  и функция экстремумов не имеет. Медиана
и функция экстремумов не имеет. Медиана  определяется из условия:
определяется из условия: Þ
Þ  Þ
Þ  .
. =
= 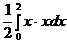 =
=  .
. найдем начальные моменты:
найдем начальные моменты:



 ,
,  ,
,  .
.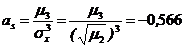 ,
,  . 3
. 3 .
. ; б)
; б)  ;
;  в)
в)  .
. .
. ; б)
; б) 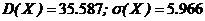 .
. .
.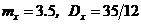 ;
;  .
.
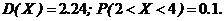
 Ответ:
Ответ: 
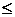 1).
1).
 Р(-1Х
Р(-1Х  Ответ:
Ответ: 




 .
.
 .
.
 ,
,  ;
;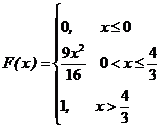 ,
,  ;
; ,
,  ;
; ,
,  .
.



 .Найти постоянный множитель С.
.Найти постоянный множитель С. . Вычислить вероятность того, что Х≤3.
. Вычислить вероятность того, что Х≤3. . Найти коэффициент а и вероятность того, что Х>1.
. Найти коэффициент а и вероятность того, что Х>1.
 СВ Х задана с точностью до множителя.Найти нормирующий множитель k, записать функцию распределения
СВ Х задана с точностью до множителя.Найти нормирующий множитель k, записать функцию распределения  , построить графики плотности распределения и функции распределения, если:
, построить графики плотности распределения и функции распределения, если: ; б)
; б)  ;
; ; г)
; г) 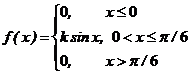 .
.


 ;
; 

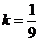 ;
; 

 ;
; 

 ; б) F(x)=
; б) F(x)=  .
. ; б)
; б) 
 .Найти дисперсию Х.
.Найти дисперсию Х. .
. Ответ: 0,188.
Ответ: 0,188. .
. . Найти моду и медиану.
. Найти моду и медиану. . Найти математическое ожидание, дисперсию, среднее квадратичное отклонение и коэффициент асимметрии величины Х.
. Найти математическое ожидание, дисперсию, среднее квадратичное отклонение и коэффициент асимметрии величины Х.
 . Найти плотность распределения вероятностей.
. Найти плотность распределения вероятностей.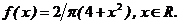
 . Определить вероятность того, что 0.2≤Х≤0.5.
. Определить вероятность того, что 0.2≤Х≤0.5.
 . Найти математическое ожидание, дисперсию и эксцесс.
. Найти математическое ожидание, дисперсию и эксцесс.
 .
. . Найти плотность вероятностей, математическое ожидание и медиану.
. Найти плотность вероятностей, математическое ожидание и медиану.
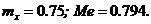
 . Найти асимметрию и эксцесс этого распределения. Ответ:
. Найти асимметрию и эксцесс этого распределения. Ответ: 