
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Плотность распределения вероятностейF(x) исчерпывающе характеризует СВ Х, однако удобнее охарактеризовать непрерывную СВ Х при помощи другой функции
откуда следует, что Свойства плотности вероятности 1) 4) Пример4.4. Дана плотность распределения вероятностей СВ Х: 4 В соответствии со свойством (3): при x £ 0 : при 0< x £ p/2: F(x)= при x> p/2: F(x)= Итак: F(x)= Числовые характеристики случайных величин. Закон распределения полностью характеризует случайную величину с вероятностной точки зрения. Однако при решении многих практических задач достаточно указать только некоторые характерные особенности распределения СВ. Это делается при помощи числовых характеристик: моды, медианы, асимметрии, эксцесса, математического ожидания, дисперсии, среднего квадратичного отклонения. Модой М0СВ Х называют наиболее вероятное ее значение. Для дискретной СВ Х модой М0 является такое ее значение, вероятность которого наибольшая. Для непрерывнойСВ Х модой М0являетсятакое ее возможное значение, которому соответствует локальный максимум плотности распределения. Медианой Мe СВ Х называется такое ее значение, относительно которого равновероятно получение большего или меньшего значения случайной этой величины: Р(Х < Мe ) =Р(Х > Мe ). (4.14)  Для непрерывной СВ медианы Мe определяется из условия:
Пример 4.6. СВ Хзадана плотностью распределения
|
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 351. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , которую называют дифференциальной функциейраспределения. Она уже не является вероятностью, т.к. в силу определения производной
, которую называют дифференциальной функциейраспределения. Она уже не является вероятностью, т.к. в силу определения производной  Отношение
Отношение  есть средняя плотность вероятности, а предел средней плотности при
есть средняя плотность вероятности, а предел средней плотности при  есть плотность распределения вероятностей СВ Х. Таким образом, по определению
есть плотность распределения вероятностей СВ Х. Таким образом, по определению (4.4),
(4.4),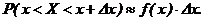
 ; 2)
; 2)  ; 3)
; 3)  ;
; ; 5)
; 5)  .
.
 . Найти функцию распределения Х.
. Найти функцию распределения Х. ;
; +
+  = sinx;
= sinx; +
+  +
+  =
= 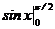 =1.
=1. . 3
. 3 ,
, 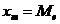 . (4.15)
. (4.15) .
.