
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Дискретные случайные величины.Простейшей формой выражения закона распределения дискретной СВ Х является таблица, в которой перечислены все возможные значения СВ
Такую таблицу ещё называют рядом распределения СВ. Все возможные значения СВ Х образуют полную группу несовместных событий, поэтому сумма всех вероятностей, помещённых в таблице равна 1, т.е.
Графически ряд распределения представляется ломаной линией, которая называется многоугольником распределения. На оси абсцисс откладываются все возможные значения х cоответствующие вероятности pi. Полученные точки ( х
4Возможными значениями СВ Хявляются: x1=0, x2=1, x3=2, x4=3, x5=4, x6=5. Вероятности этих значений можно вычислить по формуле Бернулли при P(X=0)=P5(0)= Условие все вероятности вычислены верно. Ряд распределения СВ Х имеет вид:
Многоугольник распределения изображен на рис.4.2. 3
4.3.Функция распределения.  Пусть Х - случайная величина и х - произвольное действительное число. Вероятность того, что Х примет значение, меньшее чем х, называется функцией распределения вероятностей СВ Х: F(x)=P(X<x) (4.2). Если рассматривать СВ Х как случайную точку на оси ОХ, которая в результате опыта может занять то или иное положение, то функция распределения F(x) есть вероятность того, что случайная точка Х в результате опыта окажется левее точки x (рис.4.3.1.).
1) 0£F(x)£1, поскольку является верoятностью. 2) F(x) - неубывающая функция, т.е. при 3) Функция распределения непрерывной СВ непрерывна:
5) Вероятность того, что непрерывная СВ Хпримет одно определенное значение, равна нулю: 6) Схематично функция распределения непрерывной СВ может быть представлена графиком, изображенным на рис.4.3.2. Для дискретной СВ X, которая принимает значения x1, x2, …, xn , функция распределения вычисляется согласно правила: F(x)=P(X<x)=
Пример 4.2. Производится три независимых исследования оборачиваемости средств предприятия. Вероятность ошибки при каждом исследовании равна 0,4. Построить функцию распределения СВ Х - числа ошибок. 4 Возможными значениями СВХ будут: x1=0, x2=1, x3=2, x4=3. Вероятности этих значений можно вычислить поформулеБернулли: где n=3; Получим: Р(Х=0)=0,216, Р(Х=1)=0,432, Р(Х=2)=0,288, P(X=3)=0,064. Контроль: Ряд распределения представится таблицей:
Функция распределения имеет вид: F(x) =
4Так как функция распределения непрерывной СВ Xдолжна быть непрерывной в любой точке, то:
График функции F(х)изображен на рис.4.6. На основании свойства (4) функции распределения вычислим: P(1<X<2) = F(2) ‑ F(1) = 1/4. 3 |
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 398. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
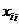 и соответствующие им вероятности
и соответствующие им вероятности 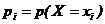 :
: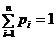 . (4.1)
. (4.1)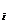 СВ X, а на оси ординат -
СВ X, а на оси ординат -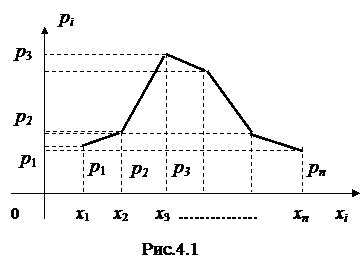
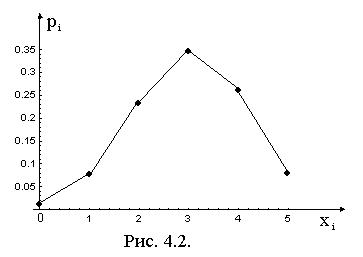 Пример 4.1. Для изучения уровня зарплаты рабочих обследовано 5 частных предприятий. Вероятность того, что на каждом из них зарплата выше среднего уровня обеспеченности, рав-на 0,6. Построить ряд расп-ределения и многоугольник распределения СВ Х - числа предприятий, на которых зарплата выше среднего уровня обеспеченности.
Пример 4.1. Для изучения уровня зарплаты рабочих обследовано 5 частных предприятий. Вероятность того, что на каждом из них зарплата выше среднего уровня обеспеченности, рав-на 0,6. Построить ряд расп-ределения и многоугольник распределения СВ Х - числа предприятий, на которых зарплата выше среднего уровня обеспеченности.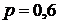 и
и 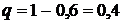 :
: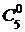 (0,6)0(0,4)5»0,0102, P(X=1)=P5(1)=
(0,6)0(0,4)5»0,0102, P(X=1)=P5(1)= 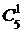 (0,6)1(0,4)4=0,0768, P(X=2)=P5(2)=
(0,6)1(0,4)4=0,0768, P(X=2)=P5(2)= 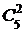 (0,6)2(0,4)3 =0,2304, P(X=3)=P5(3)=
(0,6)2(0,4)3 =0,2304, P(X=3)=P5(3)=  (0,6)3(0,4)2=0,3456, P(X=4)=P5(4)=
(0,6)3(0,4)2=0,3456, P(X=4)=P5(4)= 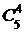 (0,6)4(0,4)1=0,2592, P(X=5)=P5(5)=
(0,6)4(0,4)1=0,2592, P(X=5)=P5(5)= 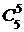 (0,6)5(0,4)0»0,0778.
(0,6)5(0,4)0»0,0778.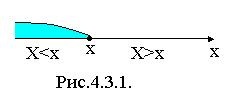 Cвойства функции распределения
Cвойства функции распределения
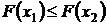 .
.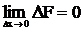 .
. 4) P(a£X<b)=F(b)-F(a).
4) P(a£X<b)=F(b)-F(a).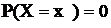 , но
, но 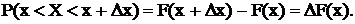
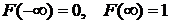 .
.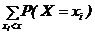 , (4.3)
, (4.3)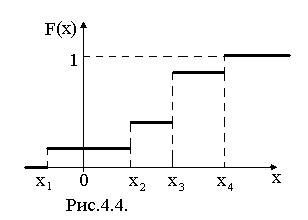 где символ xi<x под знаком суммы обозначает, что суммирование распространяется на все значения СВ, которые по своей величине меньше аргумента х. Из выражения для F(x) следует, что функция распределения дискретной СВХ разрывна и возрастает скачками при переходе через точки возможных ее значений x1, x2,...,xn, причем величина скачка равна вероятности соответствую-щего значения (рис. 4.4.).
где символ xi<x под знаком суммы обозначает, что суммирование распространяется на все значения СВ, которые по своей величине меньше аргумента х. Из выражения для F(x) следует, что функция распределения дискретной СВХ разрывна и возрастает скачками при переходе через точки возможных ее значений x1, x2,...,xn, причем величина скачка равна вероятности соответствую-щего значения (рис. 4.4.). ,
,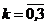 ; р = 0,4; q = 1 – 0,4 = 0,6.
; р = 0,4; q = 1 – 0,4 = 0,6.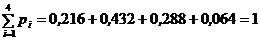 .
.
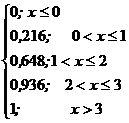 , её график представлен на рис. 4.5.3
, её график представлен на рис. 4.5.3 Пример 4.3. Функция распределения непрерывной СВ Х имеет вид: F(x) =
Пример 4.3. Функция распределения непрерывной СВ Х имеет вид: F(x) = 
 . Найти коэффициент a и построить график F(х). Определить вероятность того, что СВ в результате опыта примет значение, принадлежащее интервалу (1;2).
. Найти коэффициент a и построить график F(х). Определить вероятность того, что СВ в результате опыта примет значение, принадлежащее интервалу (1;2).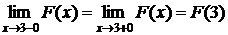 = 1 Þ a(3-1)2 = 1 Þ a=1/4.
= 1 Þ a(3-1)2 = 1 Þ a=1/4.