
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Асимптотические формулы. Локальная и интегральная теоремы Лапласа. Формула ПуассонаЕсли число испытаний достаточно велико, то при вычислении вероятностей сложных событий по формуле Бернулли возникают вычислительные проблемы, связанные с громоздкостью вычислений и с неизбежной потерей точности расчетов. Например, в рамках условий примера 3.1 вероятность того, что за год работы предприятия (288 рабочих дней) сбой в поставках сырья произойдет в 48 рабочих днях, определяется формулой: Для определения вероятностей сложных событий, подчиняющихся схеме независимых испытаний, существуют асимптотические формулы, позволяющие достаточно точно вычислить сложные вероятности в случае, если Локальная теорема Лапласа. Если вероятность наступления события А в каждом из
Существуют специальные таблицы (см. приложения), которые содержат значения функции Пример 3.3. Вероятность того, что сошедшая с конвейера деталь стандартная, равна 0.9. Деталь тут же проверяется ОТК. За смену с конвейера сходит 400 деталей. Найти вероятность того, что объем продукции, принятой ОТК за смену, составит ровно 356 деталей. 4 Из условия задачи следует, что данные испытания подчиняются схеме испытаний Бернулли: опыты независимы друг от друга, исход опыта – простое событие (есть брак или нет брака), вероятность простого события в каждом опыте одинакова и отлична от нуля или единицы. Число испытаний 
По таблицам приложения определяем значение функции
Проанализируем результат этого примера. На первый взгляд такое малое значение вероятности события, которое состоит в том, что из 400 изготовленных деталей стандартными будут 365, кажется противоречащим действительности, т.к. вероятность брака мала и равна 0.05. Но вычисленная вероятность – это вероятность только одного из 401 возможных исходов испытания, поэтому ее небольшое значение вполне оправданно. На практике обычно подобная задача ставится с условием определить возможные границы объема стандартной партии. При решении подобных задач применяется интегральная теорема Лапласа. Интегральная теорема Лапласа. Если вероятность наступления события А в каждом из
где Функция Лапласа представляет собой интеграл с переменным верхним пределом, не берущийся в рамках элементарных функций. Для вычисления его при заданном значении переменной существуют таблицы (см. приложение), в которых приведены значения интеграла Лапласа для положительных значений аргумента Пример 3.4. В условиях, заданных предыдущим примером 3.3, определить вероятность того, что число стандартных деталей, изготовленных за смену, будет соответствовать плану выпуска продукции, допускающему процент брака, не превышающий 15% от объема выпущенной продукции. 4 Согласно условию задачи, требуется найти вероятность того, что число стандартных деталей будет не меньше, чем
По таблицам находим
Ответ: с вероятностью 0.9901, т.е. 99%, план выпуска будет выполнен. Это высокая вероятность, позволяющая считать выполнение плана практически достоверным событием. 3 Формула Пуассона. Вероятность редких событий. Если вероятность простого события
Формулу Пуассона рекомендуют применять в случае, когда Пример 3.5. В торговом центре установлена электронная следящая система. Вероятность сбоя в работе системы в течение часа равна 0.004. Какова вероятность того, что за 1000 часов работы торгового центра пять раз произойдет сбой в работе следящей системы? 4 По условию,
Сравним это значение с точным значением и с вычисленным по теореме Лапласа. Точное значение вероятности вычисляется по формуле Бернулли:
Вероятность, вычисленная по теореме Лапласа, равна:
Из полученных результатов видно, что при данных значениях Задачи 3.1. В среднем по 15% договоров страховая компания выплачивает страховую сумму. Найти вероятность того, что из 10 договоров с наступлением страхового случая будет связано с выплатой страховой суммы: а) три договора; б) менее двух договоров. Ответ: а) 0,1298; б) 0,544. 3.2. В среднем пятая часть поступающих в продажу автомобилей подвергаются гарантийному ремонту. Найти вероятность того, что из 10 автомобилей подвергнутся гарантийному ремонту а) три; б) менее трех. Ответ: а) 0,201; б)0,322. 3.3. В семье 10 детей. Считая вероятности рождения мальчика и девочки равными между собой, найти вероятность того, что в данной семье а) не менее трех мальчиков; б) не более трех мальчиков. Ответ: а) 0,945; б) 0,172. 3.4. В банк отправлено 4000 пакетов денежных знаков. Вероятность того, что пакет содержит недостаточное или избыточное количество денежных знаков равно 0,0001. Найти вероятность того, что при проверке будет обнаружено: а) три ошибочно укомплектованных пакета, б) не более трех таких пакетов. Ответ: а) 0,00715; б) 0,9992. 3.5. Вероятность того, что пассажир опоздает к отправлению поезда, равна 0,01. Найти наиболее вероятное число опоздавших из 800 пассажиров и вероятность такого числа опоздавших. Ответ: 8; 0,1396. 3.6. Вероятность того, что дилер, торгующий ценными бумагами, продаст их, равна 0,7. Сколько должно быть ценных бумаг, чтобы с вероятностью 0,996 можно было утверждать, что доля проданных среди них отклонится от 0,7 не более чем на 0,03 по абсолютной величине? Ответ: 1089. 3.7. При обследовании уставных фондов банков установлено, что пятая часть банков имеют уставной фонд свыше 100 млн. грн. Найти вероятность того, что из 1800 банков имеют уставной фонд свыше 100 млн. грн. А) не менее 300; б) от 300 до 400 включительно? Ответ: 0,970; 0,961. 3.8. У страховой компании имеются 10000 клиентов. Каждый из них, страхуясь от несчастного случая, вносит 500 грн. Вероятность несчастного случая 0,0055, а страховая сумма, выплачиваемая пострадавшему, составляет 50000 грн. Какова вероятность того, что а) страховая компания потерпит убыток; б) на выплату страховых сумм уйдет более половины средств, полученных от клиентов? Ответ: 0. 3.9. По данным технического контроля 2% изготовленных автоматических станков нуждаются в дополнительной регулировке. Вычислить вероятность того, что из 6 изготовленных станков 4 нуждаются в дополнительной регулировке. Ответ: 0,0000023. 3.10. Задание состоит из 10 вопросов, предусматривающих ответы «да» или «нет». Найти наивероятнейшее число правильных ответов, студента, если он станет выбирать ответ на каждый вопрос наудачу и указать вероятность этого числа. Ответ: 3.11. Тест состоит из 10 вопросов, предусматривающих ответы «да» или «нет». Найти вероятность того, что студент, давший 8 правильных ответов, знает 8 вопросов. Причем известно, что 10% студентов знают ответы на 6 вопросов, 30% - на 7 вопросов, 30% - на 8 вопросов, а остальные знают ответы более чем на 8 вопросов. Ответ: 0,8. 3.12. На автобазе имеется 12 автомашин. Вероятность выхода на линию каждой из них равна 0,8. Найти вероятность нормальной работы автобазы в ближайший день, если для этого необходимо иметь на линии не меньше 8 машин. Ответ: 0,9274. 3.13. Вероятность того, что денежный приемник автомата при опускании одной монеты сработает правильно, равна 0,97. Сколько нужно опустить монет, чтобы наиболее вероятное число случаев правильной работы автомата было равно 100. Ответ: п = 103. 3.14. Определить вероятность того, что номер первой встретившейся автомашины не содержит: а) цифры 5; б) двух и более 5; в) ровно двух пятерок. ( Предполагается , что номер машины состоит из 4 цифр). Ответ: а)0,9 3.15. Оптовая база снабжает 10 магазинов, от каждого из которых с вероятностью 0,4 может поступить заявка на очередной день независимо от заявок других магазинов. Найти наивероятнейшее число заявок в день и вероятность получения этого числа заявок. Ответ: 3.16. На контроль поступила партия деталей из цеха. Известно, что 5% всех деталей не удовлетворяет стандарту. Каково наивероятнейшее число нестандартных деталей в партии из 1000 штук? Какова вероятность этого числа? Какова вероятность того, что в партии будет хотя бы одна нестандартная деталь? Какова вероятность того, что в партии будет не более 20 нестандартных деталей? Какова вероятность того, что в партии будет не менее 20 нестандартных деталей? Какова вероятность того, что в партии будет от 20 до 40 стандартных деталей? Ответ: 3.17. Вероятность перерасхода воды за сутки некоторым районом города равна 0,2. Найти вероятность того, что за 7 суток перерасход воды будет 1) не более чем в двух сутках; 2) не менее чем в шести сутках; 3) не более чем в пяти сутках; 4) не менее чем в двух сутках и не более чем в четырех; 5) менее чем в четырех сутках; 6) более чем в двух сутках. Найти наивероятнейшее число суток, в которых будет перерасход воды. Ответ: 1) 0,852; 2) 0,0004; 3) 0,9996; 4) 0,4186; 5) 0,9667; 6) 0,148. 3.18. Проводится социологический опрос определенной группы населения. Опрашиваемый человек с вероятностью 0.3 может оказаться студентом, с вероятностью 0.4 – служащим, с вероятностью 0.1 – бизнесменом, и с вероятностью 0.2 – пенсионером. Выбирается наугад группа из шести человек. Найти вероятности следующих событий: А={в составе группы не менее четырех служащих}; В= {в составе группы хотя бы один бизнесмен}; С={в составе группы равное число служащих и студентов}; Д={в составе группы не более двух пенсионеров}. Ответ: Р(А)=0,1792; Р(В)= 0,4686; Р(С)= 0,0346; Р(Д)= 0,9011. 3.19. Десять осветительных лампочек для освещения витрины магазина включены в цепь последовательно. Вероятность того, что лампочка перегорит при повышении напряжения в сети, одинакова для любой лампочки и равна 0.1. 1). Определить вероятность разрыва цепи при повышении напряжения в сети. 2). Вычислить вероятность разрыва цепи при числе лампочек, равном двадцати. В какой цепи (из 10 или из 20 лампочек) вероятность отказа выше? 3). Как изменятся эти вероятности, если вероятность для любой лампочки перегореть уменьшится в два раза? Ответ: 1) 0,6513; 2) 0,8784; 3) 0,4012; 0,6415. 3.20. Прибор состоит из 8 независимо работающих элементов. Вероятность отказа каждого из элементов за время Т одинакова и равна 0.2. Найти вероятность отказа прибора, если для этого достаточно, чтобы отказали хотя бы три элемента их восьми. Ответ: 0,2031. 3.21. Вероятность того, что покупателю необходима обувь 41-го размера, равна 0,2. Какова вероятность того, из пяти первых покупателей обувь этого размера понадобится; а) одному: б) по крайней мере одному из покупателей. Ответ: а) 0,4096; б) 0,6723. 3.22. Статистикой установлено, что из 1000 родившихся детей в среднем рождается 485 девочек и 515 мальчиков. В семье 5 детей. Найти вероятность того, что среди этих детей: а) 3 девочки; в) не более 3 девочек. Ответ: а) 0,3026; б) 0,8307. 3.23. Игрок выигрывает 7 копеек при появлении 6 очков на игральной кости и платит 1 копейку в других случаях. Найти вероятность того, что его выигрыш будет составлять от 16 до 30 гривен после 8000 бросаний кости. Ответ: 0,8943. 3.24. В страховом обществе застраховано 10000 лиц одного возраста и одной социальной группы. Вероятность смерти в течение года для каждого лица равна 0,006. Каждый застрахованный вносит 1 января 12 гривен страховых, и в случае его смерти родственники получают от общества 1000 гривен. Чему равна вероятность того, что: а) общество потерпит убытки; б) общество получит прибыль, не меньшую 40000, 60000, 80000 гривен? Ответ: а) событие является практически невозможным; б) 0,995; 0,5; 0,0048. 3.25. Вероятность выигрыша в некоторой лотерее на один билет равна 1/5. Предполагая, что выигрыши на различные билеты независимы, определить число билетов n, которые нужно купить, чтобы вероятность получения хотя бы одного выигрыша была не меньше 1) 0.65; 2) 0.9; 3) 0.99. Вычислить вероятность выигрыша во всех этих случаях. Ответ: 1) п=5; 0,6723; 2) п=11; 0,9141; 3) п=21; 0,9908. 3.26. На одной печатной странице 2400 знаков. При наборе текста вероятность искажения одного знака равна 1/100. Найти приближенное значение того, что на странице 1) не менее двух опечаток; 2) не более двух опечаток; 3) не менее одной и не более четырех опечаток. Найти наивероятнейшее число опечаток на странице. Ответ: 1) 0,999998; 2) 0,00002; 3) 0,00005; 3.27. Два равносильных шахматиста договорились сыграть матч из 2n результативных партий. Партии, сыгранные в ничью, не зачитываются, и предполагается, что каждый из участников может выиграть партия с вероятностью 0.5. Выигравшим матч считается тот, кто победит в большем числе партий. В каком матче больше шансов выиграть любому из участников: в матче из 8 результативных партий или из 12? Ответ: Из 12 партий.( 3.28. Компьютер состоит из 2000 элементов. Вероятность отказа одного элемента в течение одного года работы равна 0.0005 и не зависит от состояния других элементов. Какова вероятность отказа за год: 1) двух элементов; 2) не менее двух элементов; 3) не менее одного и не более трех элементов? Ответ: 1) 0,1839; 2) 0,2642; 3) 0,6131. 3.29. Завод отправил на базу 5000 доброкачественных изделий. Вероятность повреждения каждого изделия в пути равна 0,0002. Найти вероятность того, что в пути будет повреждено: а) ровно одно изделие; б) ровно 3 изделия; в) более трех изделий. Ответ: а) 0,368 б) 0,063; в) 0,019. 3.30. Учебник издан тиражом 10000 экземпляров. Вероятность того, что учебник сброшюрован неправильно, равна 0,0001. Найти вероятность того, что тираж содержит ровно 5 бракованных книг. Ответ: 0,0031. 3.31. Вероятность получения положительного результата в каждом из независимых опытов равна 0,9. Сколько нужно произвести опытов, чтобы с вероятностью 0,98 можно было ожидать, что не менее 150 опытов дадут положительный результат? Ответ: п ³ 176. 3.32. Всхожесть семян оценивается вероятностью 0,85. Вычислить вероятность того, что из 500 высеянных семян взойдет: а) 450 семян; б) от 425 до 450 семян. Ответ: а) 0, 004; б) 0,4996. 3.33. Вероятность того, что деталь не прошла проверку ОТК, равна 0,2. Найти вероятность того, что среди 400 случайно отобранных деталей непроверенными окажутся от 70 до 100. Ответ: 0,888. |
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 658. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
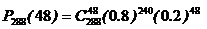 =
= 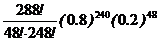 . Получить по этой формуле результат с допустимой точностью практически невозможно.
. Получить по этой формуле результат с допустимой точностью практически невозможно. велико.
велико. и отлична от нуля и единицы, а число испытаний достаточно велико, то вероятность
и отлична от нуля и единицы, а число испытаний достаточно велико, то вероятность 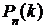 того, что в
того, что в 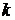 раз, приближенно равна (тем точнее, чем больше
раз, приближенно равна (тем точнее, чем больше 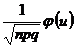 , где
, где 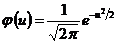 ,
,  . (3.5)
. (3.5)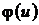 для положительных значений аргумента
для положительных значений аргумента 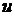 . Функция
. Функция 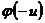 =
= 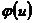 ) и ее значения при отрицательных значениях аргумента определяют по тем же таблицам.
) и ее значения при отрицательных значениях аргумента определяют по тем же таблицам.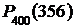 определяется по формуле:
определяется по формуле: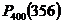 »
»  , где
, где 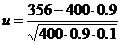 =
= 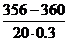 =
= 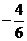 » ‑ 0.667.
» ‑ 0.667.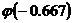 =
=  » 0.3188. Искомая вероятность
» 0.3188. Искомая вероятность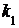 и не более
и не более 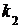 раз, приближенно равна (тем точнее, чем больше
раз, приближенно равна (тем точнее, чем больше 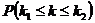 =
= 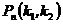 »
» 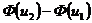 , (3.6)
, (3.6)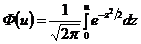 ‑ функция Лапласа,
‑ функция Лапласа,  ,
, 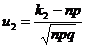 .
.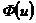 = 0.5. Интеграл Лапласа – функция нечетная (
= 0.5. Интеграл Лапласа – функция нечетная ( 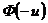 =
= 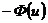 ), и для
), и для 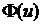 приписывают знак минус.
приписывают знак минус. = 400 ‑ 0.15×400 = 340. Верхней границей неравенства в этой задаче является объем партии
= 400 ‑ 0.15×400 = 340. Верхней границей неравенства в этой задаче является объем партии 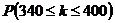 =
= 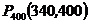 »
» 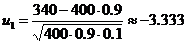 ,
, 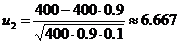 .
.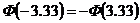 = ‑ 0.4901. Т.к.
= ‑ 0.4901. Т.к. 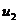 =6.67>5, то полагаем
=6.67>5, то полагаем 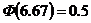 . Искомая вероятность
. Искомая вероятность =0.9901.
=0.9901.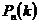 »
» 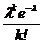 , где
, где 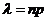 . (3.7)
. (3.7)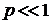 ,
, 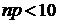 , а
, а 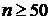 . При таких соотношениях вероятность, вычисленная по локальной теореме Лапласа, дает худшее приближение, чем вероятность, вычисленная по формуле Пуассона. Теоремой Лапласа на практике пользуются в случае npq³10.
. При таких соотношениях вероятность, вычисленная по локальной теореме Лапласа, дает худшее приближение, чем вероятность, вычисленная по формуле Пуассона. Теоремой Лапласа на практике пользуются в случае npq³10.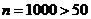 ,
, 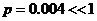 ,
, 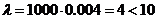 , следовательно, выполняются все условия, позволяющие применять формулу Пуассона для вычисления сложной вероятности редкого события
, следовательно, выполняются все условия, позволяющие применять формулу Пуассона для вычисления сложной вероятности редкого события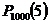 »
» 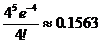 .
.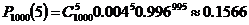
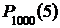 »
» 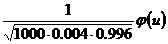 , где
, где 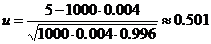 ,
, 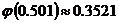 ,
, 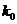 =5, р = 63/256=0,246.
=5, р = 63/256=0,246. =0,656; б) 0,9
=0,656; б) 0,9 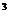 =0,948; в)1-6×0,1×0,9
=0,948; в)1-6×0,1×0,9 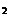 =0,951
=0,951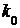 = 4; р = 0,251.
= 4; р = 0,251.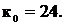
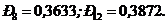 ).
).