
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Глава 3. Повторение испытанийФормула Бернулли Пусть опыт состоит в проведении серии Опыт, удовлетворяющий перечисленным условиям, называют схемой испытаний Бернулли или схемой независимых испытаний. Цель опыта: определить вероятность Эта вероятность определяется формулой Бернулли:
где Всего сложных вероятностей в схеме испытаний Бернулли всегда Сумма сложных вероятностей равна сумме вероятностей полной группы попарно несовместных событий и описывает вероятность достоверного события, равную единице:
Вероятность того, что в
Соответственно, вероятности того, что в 1) менее
2) более
3) не менее
4) не более
Пример 3.1. Вероятность того, что в течение рабочего дня произойдет сбой в поставке сырья на производство, равна 0.8. Определить вероятности того, что в течение рабочей недели (5 дней):  1) три рабочих дня не будет сбоя в поставке сырья; 2) сбой в поставках будет в трех рабочих днях; 3) сбой будет менее чем в трех рабочих днях; 4) сбой будет не более чем в одном рабочем дне; 5) сбоя в поставках не будет ни разу; 6) сбой будет хотя бы в одном рабочем дне; 7) сбой будет не менее чем в одном и не более чем в трех рабочих днях. Простое событие А = {нет сбоя в поставках сырья в течение одного рабочего дня}, Р(А)=р=0.8. Противоположное событие Р( 1) Сложное событие В={ровно три рабочих дня не будет сбоя в поставке сырья}, его вероятность вычисляем по формуле Бернулли: Р(В) = 2) Событие С= {сбой в поставках будет в трех рабочих днях}, Р(С) = 3) Событие D= {сбой в поставках будет менее чем в трех рабочих днях} равно сумме сложных событий: {сбоя не будет ни в одном дне}, {сбой будет в одном дне}, {сбой будет в двух днях}. Эти события несовместны, поэтому: P(D) = = 4) Событие F= {сбой в поставках будет не более чем в одном рабочем дне} состоит из суммы двух несовместных событий: {сбоя не будет ни в одном дне}, {сбой будет в одном дне} и его вероятность: Р(F)= = 5) Событие Е=×{сбоя поставок не будет ни в одном рабочем дне}, Р(Е)= 6) Событие G={сбой в поставках будет хотя бы в одном рабочем дне} является противоположным сложному событию Е= {сбоя не будет ни в одном дне}. Р(G) =1‑Р(Е) = 1‑0.32768 =0.67232. 7) Событие K={сбой в поставках будет не менее, чем одном, и не более, чем в трех рабочих днях}, состоит из суммы трех несовместных сложных событий: {сбой будет в одном дне}, {сбой будет в двух днях}, {сбой будет в трех днях}: Р(К) = |
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 406. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
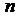 испытаний, в каждом из которых событие А может произойти с вероятностью Р(А)=р или не произойти с вероятностью Р(
испытаний, в каждом из которых событие А может произойти с вероятностью Р(А)=р или не произойти с вероятностью Р(  ) = 1 - Р(А) = 1 ‑ р = q. Если результат каждого испытания не зависит от исхода других, то испытания называются независимыми повторными испытаниями. Событие А называют простым событием. Событие ‑{ появление простого события А ровно
) = 1 - Р(А) = 1 ‑ р = q. Если результат каждого испытания не зависит от исхода других, то испытания называются независимыми повторными испытаниями. Событие А называют простым событием. Событие ‑{ появление простого события А ровно 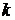 раз в
раз в 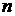 независимых испытаниях} ‑называют сложным событием и обозначают
независимых испытаниях} ‑называют сложным событием и обозначают 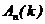 .
.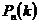 сложного события
сложного события 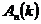 , заключающегося в том, что в
, заключающегося в том, что в  раз.
раз. , (3.1)
, (3.1) ‑ биномиальные коэффициенты.
‑ биномиальные коэффициенты. .
.
 . (3.2)
. (3.2)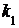 и не более
и не более 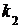 раз, равно сумме вероятностей сложных событий:
раз, равно сумме вероятностей сложных событий: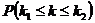 =
= 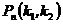 =
=  +
+  +…+
+…+  =
=  . (3.3)
. (3.3) раз
раз =
=  =
=  +
+  +…+
+…+ 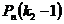 =
=  ;
; раз
раз =
=  =
=  +
+  +…+
+…+  =
=  ;
;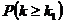 =
=  =
=  +
+  ;
; =
=  =
=  .
. ={произошел сбой в поставках сырья в течение рабочего дня},
={произошел сбой в поставках сырья в течение рабочего дня},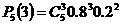 =
=  =
=  =0.2048
=0.2048 =
= 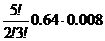 =0.0512
=0.0512 +
+  +
+  =
=  =
= +
+ 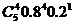 +
+  = 0.512(0.64+0.8+0.4) = 0.94208.
= 0.512(0.64+0.8+0.4) = 0.94208. +
+  =
=  =
=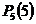 =
=  +
+ 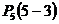 =
= 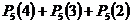 =
= 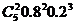 =0.82×0.2×5(0.64+2×0.8×0.2+2×0.04)== 0.64×1.04=0.6656. 3
=0.82×0.2×5(0.64+2×0.8×0.2+2×0.04)== 0.64×1.04=0.6656. 3