Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Свойства функций, непрерывных на отрезке ⇐ ПредыдущаяСтр 9 из 9 Определение. Если функция f(x) определена на отрезке [a, b], непрерывна в каждой точке интервала (a, b), в точке a непрерывна справа, в точке b непрерывна слева, то говорят, что функция f(x) непрерывна на отрезке [a, b].
1) "x0Î(a, b): 2) 3) Для функций, непрерывных на отрезке, рассмотрим некоторые свойства, которые сформулируем в виде следующих теорем, не проводя доказательств. Теорема 1. Если функция f(x) непрерывна на отрезке [a, b], то она достигает на этом отрезке своего наименьшего и своего наибольшего значения. Эта теорема утверждает (рис. 1.15), что на отрезке [a, b] найдется такая точка x1, что f(x1) £ f(x) для любых x из [a, b] и что найдется точка x2 (x2Î[a, b]) такая, что Значение f(x1) является наибольшим для данной функции на [a, b], а f(x2) – наименьшим. Обозначим: f(x1) = M, f(x2) = m. Так как для f(x) выполняется неравенство: "xÎ[a, b] m £ f(x) £ M, то получаем следующее следствие из теоремы 1. Следствие. Если функция f(x) непрерывна на отрезке, то она ограничена на этом отрезке. Теорема 2. Если функция f(x) непрерывна на отрезке [a,b] и на концах отрезка принимает значения разных знаков, то найдется такая внутренняя точка x0 отрезка Эта теорема утверждает, что график функции y = f(x), непрерывной на отрезке Теорема 3. Пусть функция f(x) непрерывна на отрезке [a, b], f(a) = A, f(b) = B и  Следствие. Если функция f(x) непрерывна на отрезке [a, b], m – наименьшее значение f(x), M – наибольшее значение функции f(x) на отрезке [a, b], то функция принимает (хотя бы один раз) любое значение m, заключенное между m и M, а потому отрезок [m, M] является множеством всех значений функции f(x) на отрезке [a, b]. Заметим, что если функция непрерывна на интервале (a, b) или имеет на отрезке В заключение рассмотрим теорему о существовании обратной функции. Напомним, что под промежутком понимается отрезок либо интервал, либо полуинтервал конечный или бесконечный.
Теорема 4. Пусть f(x) непрерывна на промежутке X, возрастает (или убывает) на X и имеет множеством значений промежуток Y. Тогда для функции y = f(x) существует обратная функция x = j(y), определенная на промежутке Y, непрерывная и возрастающая (или убывающая) на Y с множеством значений X. Замечание. Пусть функция x = j(y) является обратной для функции f(x). Так как обычно аргумент обозначают через x, а функцию через y, то запишем обратную функцию в виде y = j(x). Пример 1. Функция y = x2 (рис. 1.8, а) на множестве X = [0, +¥) непрерывна, возрастает и имеет множеством значений Y = [0, +¥). Функция y = x2 имеет обратную функцию x =
Пример 2. Функция y = sinx (рис. 1.19, а) непрерывна, возрастает на отрезке [–  , ,  ] и имеет множеством значений отрезок [–1, 1], поэтому она имеет обратную функцию y = arcsinx (рис. 1.19, б), определенную, непрерывную и возрастающую на отрезке [–1, 1] и имеющую множество значений [– ] и имеет множеством значений отрезок [–1, 1], поэтому она имеет обратную функцию y = arcsinx (рис. 1.19, б), определенную, непрерывную и возрастающую на отрезке [–1, 1] и имеющую множество значений [–  , ,  ]. ].
Заметим, что графики взаимно обратных функций симметричны относительно прямой y = x. Предлагаем построить графики взаимно обратных функций: 1) y = cosx, y = arccosx; 2) y = tgx, y = arctgx; 3) y = ctgx, y = arcctgx; 4) y = ex, y = lnx.
Введение............................................................................................................................................................................. 3 ГЛАВА 1. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ................................................................................... 4 1.1. Логическая и математическая символика....................................................................................................................... 4 1.2. Множества....................................................................................................................................................................... 5 1.3. Функции.......................................................................................................................................................................... 7 1.4. Пределы функции на бесконечности.............................................................................................................................. 8 1.5. Предел функции в точке............................................................................................................................................... 11 1.6. Бесконечно-малые функции и их свойства................................................................................................................... 14 1.7. Бесконечно большие функции, их свойства и связь с бесконечно малыми функциями............................................. 17 1.8. Основные теоремы о пределах..................................................................................................................................... 18 1.9. Первый замечательный предел..................................................................................................................................... 21 1.10. Второй замечательный предел.................................................................................................................................... 22 1.11. Сравнение бесконечно малых функций. Эквивалентные бесконечно малые функции.............................................. 24 1.12. Непрерывность функции в точке. Точки разрыва....................................................................................................... 26 1.13. Свойства функций, непрерывных на отрезке.............................................................................................................. 29
|
|||||||||||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 363. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 Другими словами, функция f(x) непрерывна на отрезке [a, b], если выполнены три условия:
Другими словами, функция f(x) непрерывна на отрезке [a, b], если выполнены три условия: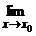 f(x) = f(x0);
f(x) = f(x0);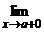 f(x) = f(a);
f(x) = f(a);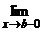 f(x) = f(b).
f(x) = f(b).
 (рис. 1.8, б), а после переобозначения переменных y =
(рис. 1.8, б), а после переобозначения переменных y = 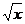 , определенную, непрерывную и возрастающую на X.
, определенную, непрерывную и возрастающую на X.