
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Первый замечательный пределРассмотрим функцию y =
Доказательство 1) Пусть a – положительный острый угол, докажем Рассмотрим окружность радиуса R (рис. 1.12), OA = OC = R, тогда длина дуги АС равна: R×a, АВ = R×sina. Так как |AB| < |
Вычислим теперь Из рис. 1.12 видим, что SDOAC < SсекторOAC < SDODC. (*) SDOAC = Подставляя последние выражения в неравенства (*), находим:
Деля все части неравенства (**) на положительное число 1 < Применяя к неравенству (***) теорему о сжатой переменной при a ® 0 получим:
2) Пусть x < 0, x = –a, тогда a > 0, Итак, доказано, что С помощью этого предела находятся многие другие пределы, содержащие тригонометрические функции. Второй замечательный предел Ранее рассматривались понятия последовательности (как функции натурального аргумента), предела последовательности (см. разд. 1.3, 1.4). Рассмотрим возрастающую последовательность:  Теорема 1 (достаточный признак существования предела последовательности) Всякая возрастающая ограниченная сверху последовательность имеет предел. Применим эту теорему для доказательства следующей теоремы. |
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 352. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
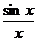 , аргумент x (как всегда в математическом анализе) выражается в радианах. При x = 0 функция
, аргумент x (как всегда в математическом анализе) выражается в радианах. При x = 0 функция 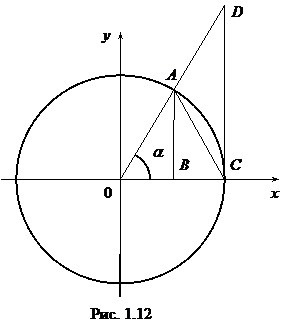 Теорема.
Теорема. 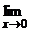
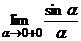 = 1. Предварительно докажем, что
= 1. Предварительно докажем, что 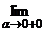 sina = 0 и
sina = 0 и 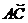 |, то 0 < sina < a. Если a ® 0, то по теореме 8 (разд. 1.8)
|, то 0 < sina < a. Если a ® 0, то по теореме 8 (разд. 1.8) 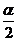 , то на основании теорем о пределах получим:
, то на основании теорем о пределах получим: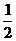 R2sina, SсекторOAC=
R2sina, SсекторOAC= 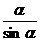 <
< 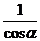 или 1 >
или 1 > 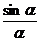 > cosa (***)
> cosa (***)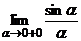 = 1 (ведь
= 1 (ведь 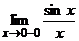 =
= 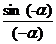 =
= 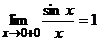 , а потому
, а потому 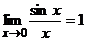 .
.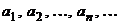 Для нее
Для нее 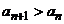 для любого натурального n. Если эта последовательность не является ограниченной, то она не имеет предела, так как ее члены неограниченно возрастают. Если же возрастающая последовательность ограничена, то она имеет предел.Этот факт доказывается в полных курсах математического анализа [6], мы приведем лишь его полную формулировку.
для любого натурального n. Если эта последовательность не является ограниченной, то она не имеет предела, так как ее члены неограниченно возрастают. Если же возрастающая последовательность ограничена, то она имеет предел.Этот факт доказывается в полных курсах математического анализа [6], мы приведем лишь его полную формулировку.