
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Непрерывность функции в точке. Точки разрываПусть функция f(x) определена в точке x0 и некоторой ее окрестности. Если существует На языке логики равенство "e>0 $d>0 "xÎ(x0 – d, x0 + d) |f(x) – f(x0)| < e . Используя понятия односторонних пределов, можно перефразировать определение так: функция называется непрерывной в точке x0, если она определена в точке x0 и некоторой ее окрестности, если существуют
Иногда приходится рассматривать непрерывность функции в точке x0 справа или слева. Пусть функция определена в точке x0 и некоторой ее левой полуокрестности. Если Аналогично определяется непрерывность справа. Пример 1. Функция f(x) = x3 определена на R. Покажем, что f(x) непрерывна в точке x0 = 2. Действительно, f(2) = 23 = 8, Пример 2. f(x) = Покажем, что f(x) непрерывна в точке x0 = 0: f(0) = 0, Так как Дадим определение точек разрыва. Пусть f(x) определена в окрестности точки x0, но может быть не определена в x0. Точка x0 называется точкой разрыва для функции f(x), если в точке x0 функция f(x) не определена, или Пример 3. Функция f(x) = Пример 4. Функция f(x) = Пример 5. Пусть E(x) = «целая часть числа x», т.е. E(x) равно наибольшему целому числу, не превосходящему x0. Так E 
Точка разрыва x0 для функции f(x) называется точкой разрыва первого рода, если существуют (конечные) пределы: Точка x0 разрыва первого рода, для которой Рассмотрим операции над непрерывными функциями. Теорема 1. Если функции f1(x) и f2(x) непрерывны в точке x0, то их сумма и произведение также непрерывны в точке x0. Если, кроме того, f2(x0) ¹ 0, то частное Доказательство. Доказательство основано на свойствах пределов. Докажем, например, что сумма непрерывных функций непрерывна. Функции f1(x), f2(x) непрерывны в точке x0, поэтому
что означает непрерывность f1(x) + f2(x) в точке x0. Аналогично для других утверждений теоремы. Заметим, что формулу Теорема 2. Если функция u = j(x) непрерывна в точке x0, а функция y = f(u) непрерывна в точке u0 = j(x0), то сложная функция y = f(j(x)) непрерывна в точке x0. Доказательство. Покажем, что
Теорема доказана. Установим непрерывность некоторых элементарных функций: 1. Всякая постоянная функция y = C непрерывна в каждой точке x0ÎR, так как 2. Функция y = x непрерывна в любой точке x0, так как 3. Любой многочлен: y = a0 + a1x + a2x2 + ...+ anxn, непрерывен в каждой точке числовой оси, как сумма непрерывных функций. 4. Всякая рациональная дробь, являющаяся отношением двух многочленов 5. Функция y = sinx, y = cosx непрерывны в точке x0 = 0, так как
(Это было доказано в разд. 1.9 ). Сформулируем без доказательств следующую теорему. Теорема 3. Всякая элементарная функция непрерывна в каждой точке, в которой она определена. Если функция f(x) непрерывна в каждой точке интервала (a, b), то говорят, что f(x) непрерывна на интервале (a, b). Пример 6. Функция f(x) = |
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 330. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 и
и  , то функция f(x) называется непрерывной в точке x0, а x0 называется точкой непрерывности функции f(x).
, то функция f(x) называется непрерывной в точке x0, а x0 называется точкой непрерывности функции f(x). f(x),
f(x),  f(x) и
f(x) и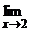 f(x) =
f(x) = 
 .
.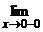 f(x) =
f(x) =  f(x) =
f(x) = 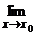 f(x) не существует, или
f(x) не существует, или 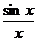 не определена в точке x0 = 0, но определена в любой окрестности этой точки, поэтому x0 = 0 является точкой разрыва для f(x).
не определена в точке x0 = 0, но определена в любой окрестности этой точки, поэтому x0 = 0 является точкой разрыва для f(x). не определена в точке x0 = 3, x0 = 3 – точка разрыва для f(x).
не определена в точке x0 = 3, x0 = 3 – точка разрыва для f(x). = 1, E(5) = 5, E(p) = 3, E(0) = 0,
= 1, E(5) = 5, E(p) = 3, E(0) = 0,  E(x) = 1,
E(x) = 1,  Так как
Так как  E(x), то E(x) в точке x0 = 2 имеет разрыв, как и в любой другой целочисленной точке. Различают точки разрыва первого рода и второго рода.
E(x), то E(x) в точке x0 = 2 имеет разрыв, как и в любой другой целочисленной точке. Различают точки разрыва первого рода и второго рода. f(x) и
f(x) и  f(x). В противном случае x0 – точка разрыва второго рода. В примере 5 точка x0 = 2 является точкой разрыва первого рода, так как существуют пределы
f(x). В противном случае x0 – точка разрыва второго рода. В примере 5 точка x0 = 2 является точкой разрыва первого рода, так как существуют пределы  = –¥,
= –¥,  = +¥.
= +¥. , то j(x) непрерывна в точке x0 = 0, так как
, то j(x) непрерывна в точке x0 = 0, так как  j(x) = =
j(x) = =  также непрерывно в точке x0.
также непрерывно в точке x0.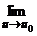 f(u) = f(u0) = f(j(x0)).
f(u) = f(u0) = f(j(x0)). , непрерывна во всех точках, в которых многочлен Q(x) не обращается в 0.
, непрерывна во всех точках, в которых многочлен Q(x) не обращается в 0.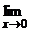 sinx = 0, sin0 = 0,
sinx = 0, sin0 = 0,  = f(x0).
= f(x0).