
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Логическая и математическая символикаСтр 1 из 9Следующая ⇒ Введение Данное пособие является составной частью учебного комплекса по курсу высшей математики, которое может быть полезно для организации учебного процесса на факультете дистанционного обучения при самостоятельной подготовке студентов к экзаменам. Оно поможет без помощи преподавателя организовать планомерное изучение материала не только основных понятий и положений теории, но и основных приемов и методов решения задач. В учебном пособии рассматриваются следующие темы: введение в математический анализ, дифференциальное исчисление функций одной переменной, на которых базируется вся математика. Учебное пособие создано на основе опыта преподавания высшей математики в Комсомольском-на-Амуре государственном техническом университете на технических и гуманитарных факультетах. Теоретический материал иллюстрируется большим количеством примеров и задач различной трудности. После каждого раздела приводятся экзаменационные вопросы. Более подробное изложение данного материала можно найти в книгах, учебных пособиях и монографиях, указанных в списке литературы. Специфика работы с пособием состоит в том, что сначала необходимо ознакомиться с базовыми понятиями и методами математического анализа, изложенными в соответствующих разделах, затем изучить практическую часть (главу 3), а затем перейти к выполнению контрольной работы, предусмотренной программой. Выполненную контрольную работу следует направить на рецензирование. В случае если рецензент обнаружит ошибки в контрольной работе, рекомендуется проработать материал до полного усвоения неясностей, сделать работу над ошибками в той же тетради, в которой была выполнена контрольная работа, и вернуть ее на повторное рецензирование.  Последним этапом работы с данным пособием является экзамен (зачет), вопросы к которому также приведены в заключительной части данного пособия. ГЛАВА 1. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ Логическая и математическая символика В математике употребляются специальные символы, позволяющие сократить запись и точнее выразить утверждение. Математические символы: Например, применяя символ «>» к числам a, b, получим запись «a > b», которая является сокращением для предложения: «число a больше числа b». Если Наряду с математической символикой в математике широко используется логическая символика, применяемая к высказываниями предикатам. Под высказыванием понимается предложение, которое либо только истинно, либо только ложно. Например, высказывание «–3 > 0» ложно, а высказывание «2 Предикат – это предложение с одной переменной или несколькими переменными. Например, предложение: «число x больше числа 0» (в символах x > 0) является предикатом от одной переменной x, а предложение: «a + b = c» – предикат от трех переменных a, b, c. Предикат при конкретных значениях переменных становится высказыванием, принимая истинное и ложное значение. Будем обозначать предикаты как функции: Q(x) =«x > 0», F(x,b,c) = «x + b = c». Логические символы: 1. Отрицание применяется к одному высказыванию или предикату, соответствует частице «не» и обозначается Например, формула 2. Конъюнкцияприменяется к двум высказываниям или предикатам, соответствует союзу «и», обозначается: А & B (или A Так формула (–3 > 0) & (2 3. Дизъюнкцияприменяется к двум высказываниям или предикатам, соответствует союзу «или» (неразделительному) и обозначается A Предложение: «число x принадлежит множеству 4. Импликациясоответствует союзу «если ..., то ...» и обозначается: A Так, запись «a > –1 5. Эквиваленция A Символы 6. Квантор общности применяется к предикату F(x, ...), содержащему одну переменную (например, x) или несколько переменных, при этом получается формула Например: 7. Квантор существования, примененный к предикату F(x,...) соответствует предложению «существует x, такой, что F(x,...)» («найдется x, для которого F(x,...)») и обозначается: Например, истинное высказывание «существует действительное число, квадрат которого равен 2» записывается формулой Если квантор применяется к предикату с одной переменной, то получается высказывание, истинное или ложное. Если квантор применяется к предикату с двумя или большим числом переменных, то получается предикат, в котором переменных на одну меньше. Так, если предикат F(x, y) содержит две переменные, то в предикате Так, предикат «|sinx| < a» содержит две переменные x, a. Предикат Если к предикату Для некоторых формул введем сокращенную запись. Так, вместо формулы вместо Формулу Будем называть Несколько кванторов общности (существования) заменяем на один: вместо Множества Понятие множества является первоначальным понятием математики, точное определение ему не дается, но его можно пояснить, описать через другие понятия. Можно сказать, что множество – это совокупность, собрание каких-то объектов, предметов, при этом объект, входящий в это множество, называют его элементом. Множества могут содержать как конечное число элементов, так и бесконечно много элементов. Рассматривают и множество, не содержащее элементов, его называют пустым и обозначают символом Æ. В математическом анализе чаще всего рассматриваются числовые множества, за некоторыми из них закреплены специальные обозначения. Так, множество всех натуральных чисел обозначаются через N и записывают так: N = {1,2,3,...}. Далее, через Z обозначают множество всех целых чисел, содержащее как натуральные числа, так и 0, и целые отрицательные числа; Z= {..., –3, –2, –1, 0, 1, 2, 3, ...}. Рациональным называется число, которое можно представить в виде отношения двух целых чисел: Известно, что любое рациональное число можно представить десятичной дробью, конечной и бесконечной периодической. Например, рациональное число 5/6 представимо бесконечной периодической дробью 5/6 = 0,83333..., а число 3/8 = 0,375. В последнем случае можно считать десятичную дробь тоже бесконечной с числом 0 в периоде: 3/8 = 0,3750000... . Известно, что всякую периодическую бесконечную дробь можно обратить в обыкновенную дробь p/q. Иррациональным числом называется всякая бесконечная непериодическая десятичная дробь. Множество всех рациональных и иррациональных чисел называется множеством действительных чисел и обозначается через R. Иными словами, множество действительных чисел R – это множество всех бесконечных десятичных дробей. Пусть M1, M2 – некоторые множества. Если каждый элемент множества M1 является элементом множества M2, то говорят, что M1 есть подмножество множества M2 и обозначается M1 Ì M2. Итак, M1 Ì M2 тогда и только тогда, когда "x(xÎM1 ® xÎM2). Из определения числовых множеств можно заключить, что N Ì Z, Z Ì Q, Q Ì R. Множество действительных чисел является подмножеством множества C всех комплексных (о которых мы сейчас говорить не будем), т.е. R Ì C. Часто рассматриваются подмножества действительных чисел (a, b), [a, b], [a, b), (a, b] называемые, соответственно, интервалом, отрезком, полуинтервалом. Дадим символические определения этих множеств, а слово «называется» заменим на знак (a, b) (a, b] Заметим, что на числовой оси каждое действительное число изображается определенной точкой и любая точка числовой оси задает некоторое число, поэтому [a, b] изображается множеством всех точек отрезка, вместе с концами a, b, в то время как (a, b) – множеством точек отрезка без концов a, b. Объединение AÈB, пересечение AÇB Рассмотрим операции множеств A,B давая им символические определения: AÈB Иногда рассматривается операция разности множеств A и B, это множество элементов A, не входящие в B. Обозначение: A\B. Таким образом, A \ B Функции Пусть x, y – переменные величины. Если каждому значению переменных x из множества A соответствует по определенному закону единственное значение переменной y, то говорят, что y является функцией (однозначной) от x и пишут y = f(x) или Пример 1. Для функции y = Пример 2. y = Замечание. Иногда рассматривают многозначные функции, допуская, что каждому значению xÎA, соответствует одно или более одного значений y. Мы в дальнейшем под функцией будем понимать однозначную функцию. Способы задания функции Аналитический способ: связь между аргументом x и функцией y задается формулой, при этом на разных участках области определения она может задаваться различными формулами (см. пример 2) . В примерах 1, 2 функции заданы аналитически. Табличный способ: функция задается таблицей отдельных значений аргумента и соответствующих значений функции. Такими являются таблицы тригонометрических функций, таблицы логарифмов и т.д. Графический способ: в этом случае соответствие между значениями x и y задается с помощью графика. Среди числовых функций особое место занимают функции с областью определения A = N. Пусть аргумент функции f(x) принимает только значения 1, 2, 3,....n,... Обозначим f(1) = a1, f(2) = a2, ..., f(n) = an, ... Такую функцию называют последовательностью, a1 – первый член, ..., an – n-й член этой последовательности. Рассмотрим свойства, которыми могут обладать (или не обладать) некоторые функции. Функция f(x) называется возрастающейна множестве M (строго), если большему значению аргумента соответствует большее значение функции. Символически это может быть записано так: "x1, x2ÎM(x1 < x2 ® f(x1) < f(x2)). Функция f(x) называется убывающей (строго) на множестве M, если большему значению аргумента соответствует меньшее значение функции. Символически: Функция, убывающая или возрастающая на множестве M, называется монотонной на множестве M. В качестве примера рассмотрим функцию y = x2. На интервале (–¥, 0) это убывающая функция, а на интервале (0, + ¥ ) – возрастающая. Функция f(x) называется ограниченной сверху на множестве M, если существует такое число k, что для любого значения xÎM f(x) < k. Символически это может быть записано так: $k "xÎM (f(x) < k). Аналогично дается определение функции, ограниченной снизу. Если функция ограничена и сверху, и снизу, то она называется ограниченной. Так, функция y = Функция f(x) называется четной, если "xÎA (f(–x) = f(x)), и называется нечетной, если "xÎA (f(–x) = –f(x)). Например, функция y = x2 является четной, а y = sinx – нечетной. Функция f(x) называется периодической с периодом T (T ¹ 0 ), если Известно, что все тригонометрические функции являются периодическими. Введем важные понятия сложной и обратной функции. Если переменная y является функцией от x, y = f(x); а x – функция от переменной t: x = j(t), то y = f(j(t)) является функцией от t и называется сложной функцией или функцией от функции. Например, пусть y = x2, x = sint, тогда функция y = (sint)2 является сложной. Пусть y = f(x) с областью определения A и множеством значений B такова, что для любого значения yÎB существует единственное значение xÎB, такое, что f(x) = y, тогда переменная x является функцией от y, обозначим x = j(y). Эту функцию называют обратной для y = f(x). Для обратной функции x = j(y) область определения B, а множество значений A. Иногда функцию, обратную к функции y = f(x), обозначают: Например, для функции y = x2 с областью определения [0, +¥) и таким же множеством значений обратной является функция: x =
Абсолютной величиной числа a называется неотрицательное число, обозначаемое |a|, такое, что |a| = Неравенство |x| < m ( m > 0 ) равносильно двойному неравенству –m < x < m, неравенство |x – x0| < e (e > 0) равносильно x0 – e < x< x0 + e. Множество точек с таким свойством (рис. 1.1) является интервалом (x0 – e, x0 + e) и называется e – окрестностью точки x0 (рис. 1.1). |
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 309. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 – обозначения прямых, то запись
– обозначения прямых, то запись  есть утверждение, что
есть утверждение, что  параллельна
параллельна  . Запись «x
. Запись «x  M» означает, что x является элементом множества M.
M» означает, что x является элементом множества M. 2 = 4» истинное. Будем высказывания обозначать большими латинскими буквами, возможно с индексами. Например, A = «–3 > 0», B = «2
2 = 4» истинное. Будем высказывания обозначать большими латинскими буквами, возможно с индексами. Например, A = «–3 > 0», B = «2 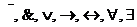 .
. .
. есть сокращение для предложения: «–3 не больше 0» («неверно, что –3 больше 0»).
есть сокращение для предложения: «–3 не больше 0» («неверно, что –3 больше 0»).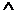 B).
B). B .
B . или множеству
или множеству  » изображается формулой:
» изображается формулой:  .
. B.
B.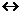 B соответствует предложению: «A тогда и только тогда, когда B».
B соответствует предложению: «A тогда и только тогда, когда B». называются кванторами общности и существования, соответственно применяются к предикатам (а не к высказываниям). Квантор
называются кванторами общности и существования, соответственно применяются к предикатам (а не к высказываниям). Квантор  читается, как «любой», «каждый», «все», или с предлогом «для»: «для любого», «для всех» и т.д. Квантор
читается, как «любой», «каждый», «все», или с предлогом «для»: «для любого», «для всех» и т.д. Квантор  читается: «существует», «найдется» и др.
читается: «существует», «найдется» и др. xF(x,...).
xF(x,...). xF(x, y)или
xF(x, y)или  xF(x, y) является высказыванием.
xF(x, y) является высказыванием. этот предикат обращается в ложное высказывание
этот предикат обращается в ложное высказывание  ), при а = 2 получаем истинное высказывание
), при а = 2 получаем истинное высказывание  , выражающую истинное высказывание: «функция sinx является ограниченной».
, выражающую истинное высказывание: «функция sinx является ограниченной». 0) сократим так:
0) сократим так:  и т.д. ограниченными кванторами.
и т.д. ограниченными кванторами. пишем
пишем  будем писать
будем писать  .
. (pÎZ, qÎZ, q¹0). Множество всех рациональных чисел обозначается через Q. Символически определение множества рациональных чисел можно записать так: Q
(pÎZ, qÎZ, q¹0). Множество всех рациональных чисел обозначается через Q. Символически определение множества рациональных чисел можно записать так: Q  {
{  :
: }. В частном случае R \ Q есть множество иррациональных чисел.
}. В частном случае R \ Q есть множество иррациональных чисел. область определения A= (–¥, –1]È[1, +¥), множество значений B= [0, +¥).
область определения A= (–¥, –1]È[1, +¥), множество значений B= [0, +¥). , A= R, B= (–¥, +1].
, A= R, B= (–¥, +1]. .
. .
. В дальнейшем часто будет использоваться понятие абсолютной величины числа, а также понятие e – окрестности точки.
В дальнейшем часто будет использоваться понятие абсолютной величины числа, а также понятие e – окрестности точки. .
.