
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Пределы функции на бесконечностиРассмотрим одно из центральных понятий математического анализа – понятие предела функции. Ввиду сложности для понимания этого понятия сначала дадим его описательное определение, подкрепленное примерами, а затем строгое определение. Предел функции при x ® +¥ Пусть функция y = f(x) определена на множестве всех действительных чисел R или на бесконечном интервале (a, +¥). Число b называют пределом функции f(x)при стремлении x к +¥ (x® +¥), если значения f(x) приближаются к числу b как угодно близко при достаточно больших x. Обозначение: Пример 1. Функция y =
Из таблицы видно, что значения функции приближаются к числу 2 с увеличением x.
Разность Пусть e – произвольное (малое) положительное число, тогда найдется такое x0, что f(x) – 2 < e для всех x > x0. Действительно, f(x) – 2 = Пример 2. Функция y =
 Из таблицы значений и графика (рис. 1.3) видим, что с ростом x значения f(x) приближаются к 1, оставаясь меньше 1. Покажем, что
Покажем, что |f(x) – 1| может стать меньше любого заданного положительного числа e при достаточно больших x. Для этого решим неравенство
Если x > 298, то Дадим строгое определение предела функции при x® +¥. Число b называется пределом функции f(x) при стремлении x к +¥, если для любого положительного числа e найдется такое число x0, что для всех x, больших x0, выполняется неравенство: f(x) – b | < e . Геометрическая интерпретация этого определения приведена на рис. 1.4. В логических символах это определение выглядит так:
Пример 3. Доказать, что
| f(x) – 0 | = Обозначим: x0 = Пусть для некоторой функции y = f(x) Предел последовательности Как отмечалось раньше, любая последовательность a1, a2, ..., an , ... есть функция натурального аргумента, an = f(n), n Î N. Определение предела последовательности почти дословно повторяет определение предела функции при x®+Ґ. Число b называется пределом последовательности {an}, если для любого e > 0 существует такое натуральное число n0, что для всех натуральных n, больших n0, выполняется неравенство: | an – b | < e. Обозначение: Доказать самостоятельно, что Предел функции при x® -¥ Пусть функция y = f(x) определена на R или (–¥, a). Число b называется пределом функции f(x) при стремлении x к –¥ (x ® –¥), если для любого положительного числа e существует такое x0, что для всех x, меньших x0, выполняется неравенство:
y = b + e, y = b – e. Доказать самостоятельно, что Рассмотренные пределы объединяются общим названием «пределы на бесконечности». Не надо думать, что любая функция, определенная на R, имеет предел при x ® +¥ или x ® –¥. Например, Предел функции в точке Пусть функция f(x) определена в некоторой окрестности точки x0 (возможно, определена на R), но в самой точке x0 функция f(x) может быть и не определена. Дадим сначала описательное определение предела функции в точке и приведем пример. Число b называется пределом функции f(x) в точке x0 (x ® x0), если значения f(x) приближаются к числу b как угодно близко при условии, что значения аргумента x подходят к x0 достаточно близко. Обозначение: Пример 1. Функция y =
График функции: y =
Потребуем, чтобы |f(x) – 4| < Аналогично можно показать, что |f(x) – 4| < Дадим строгое определение предела функции в точке. Число b называется пределом функции f(x) в точке x0 (при стремлении x к x0), если для любого положительного числа e найдется положительное число d, такое, что для любого x ¹ x0 и удовлетворяющему неравенству: x0 – d < x < x0 + d, выполняется неравенство: | f(x) – b| < e. Символически "e > 0 $d > 0 "x ¹ x0 (x0 – d < x < x0 + d ® | f(x) – b | < e). (*)
«x ¹ x0 и x0 – d < x < x0 + d» можно записать в виде неравенства: 0 < | x – x0 | < d , и тогда формула (*) примет вид: "e > 0 $d > 0 "x (0 < | x – x0 | < d ® | f(x) – b | < e). Если Пример 2. Показать, что В самом деле f(x) = x, поэтому для любого e > 0: | f(x) – x0 | < e при условии | x – x0 | < e (здесь d = e). |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 340. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
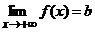 .
.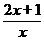 определена на интервале (0, +¥). Составим таблицу ее некоторых значений и построим ее график (рис. 1.2):
определена на интервале (0, +¥). Составим таблицу ее некоторых значений и построим ее график (рис. 1.2):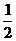
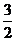
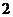
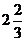
 Убедимся, что
Убедимся, что 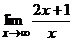 = 2.
= 2.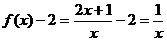 показывает, на сколько отличается f(x) от 2. Так, если x равно 10, то f(x) отличается от 2 на 1/10, а если x = 100, то f(x) – 2 = 1/100. Разность
показывает, на сколько отличается f(x) от 2. Так, если x равно 10, то f(x) отличается от 2 на 1/10, а если x = 100, то f(x) – 2 = 1/100. Разность 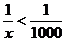 , отсюда x > 1000.
, отсюда x > 1000. ,
,  . Обозначив x0 =
. Обозначив x0 = 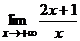 = 2.
= 2.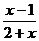 определена на (–2, +¥). Выпишем таблицу ее некоторых значений и построим график (рис. 1.3).
определена на (–2, +¥). Выпишем таблицу ее некоторых значений и построим график (рис. 1.3).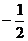
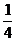
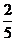
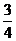
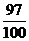
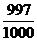
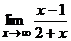 =1. Разность f(x) – 1 отрицательна, поэтому вычислим ее абсолютную величину:
=1. Разность f(x) – 1 отрицательна, поэтому вычислим ее абсолютную величину: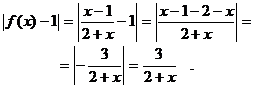
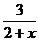 < e, получим: 2 + x >
< e, получим: 2 + x > 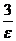 , и x >
, и x > 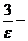 2. Таким образом, если x > x0, то
2. Таким образом, если x > x0, то 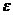 . Например, возьмем в качестве e число 0,01, тогда:
. Например, возьмем в качестве e число 0,01, тогда: x0 =
x0 = 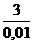 – 2 = 300 – 2 = 298, x0 = 298.
– 2 = 300 – 2 = 298, x0 = 298.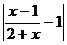 < 0,01. Этим мы показали, что
< 0,01. Этим мы показали, что 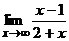 = 1 (рис. 1.3).
= 1 (рис. 1.3). f(x) = b означает "e > 0 $x0 "x > x0 ( | f(x) – b | < e ).
f(x) = b означает "e > 0 $x0 "x > x0 ( | f(x) – b | < e ).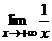 = 0 x Î (0, +¥).
= 0 x Î (0, +¥).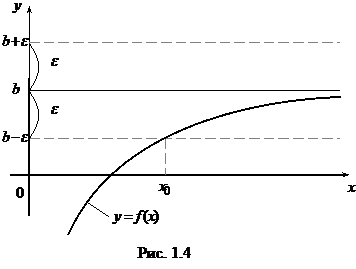 Доказательство:f(x) =
Доказательство:f(x) = 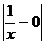 =
= 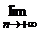 an = b.
an = b.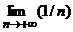 = 0.
= 0.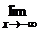 f(x) = b.
f(x) = b.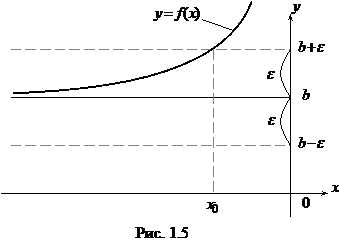 Геометрически этот факт означает, что точки графика y = f(x) (рис. 1.5) приближаются как угодно близко к соответствующим точкам прямой y = b при движении x влево неограниченно и что по фиксированному e > 0 найдется число x0, такое, что для всех x, меньших x0, график y = f(x) заключен внутри полосы, ограниченной прямыми:
Геометрически этот факт означает, что точки графика y = f(x) (рис. 1.5) приближаются как угодно близко к соответствующим точкам прямой y = b при движении x влево неограниченно и что по фиксированному e > 0 найдется число x0, такое, что для всех x, меньших x0, график y = f(x) заключен внутри полосы, ограниченной прямыми: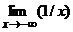 = 0
= 0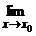 f(x) = b.
f(x) = b.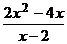 определена во всех точках числовой оси, за исключением x0 = 2. Найдем
определена во всех точках числовой оси, за исключением x0 = 2. Найдем 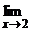 f(x), для этого вычислим значения f(x) для x, близких к 2, и построим график: y = f(x). Заметим, что для x ¹ 2:
f(x), для этого вычислим значения f(x) для x, близких к 2, и построим график: y = f(x). Заметим, что для x ¹ 2: 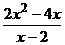 = 2x.
= 2x. Покажем, что
Покажем, что 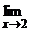
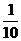 , тогда из неравенства: |2x – 4| <
, тогда из неравенства: |2x – 4| <  . Т.е. при значениях x, удовлетворяющих неравенству: 2 –
. Т.е. при значениях x, удовлетворяющих неравенству: 2 – 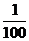 , если 2 –
, если 2 – 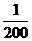 < x < 2 +
< x < 2 + 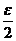 < x < 2 +
< x < 2 + 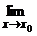 f(x) = b означает:
f(x) = b означает: Заметим, что условие:
Заметим, что условие: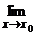 f(x) = b, то на графике функции y = f(x) (рис. 1.7) это иллюстрируется (по определению предела) так: для всех точек x, отстоящих от x0 не далее, чем на d, значения f(x) отличаются от b не более чем на e.
f(x) = b, то на графике функции y = f(x) (рис. 1.7) это иллюстрируется (по определению предела) так: для всех точек x, отстоящих от x0 не далее, чем на d, значения f(x) отличаются от b не более чем на e.